백준 3080 - 아름다운 이름
문자열 알고리즘 관련 문제들을 많이 풀고 있습니다. 저번엔 접미사 배열로 글을 썼는데, 이번엔 Trie와 관련된 문제인 아름다운 이름를 풀어봤습니다. 접두사가 같은 이름들끼리는 인접하게 번호를 붙일 때, 그 순열의 개수를 구해야 합니다. 이름의 개수는 최대 삼천 개니까, 브루트포스로는 어림도 없겠죠?
저번에 풀어봤던 Prefix free subsets과 비슷하게 트라이로 풀 수 있을 것 같습니다.
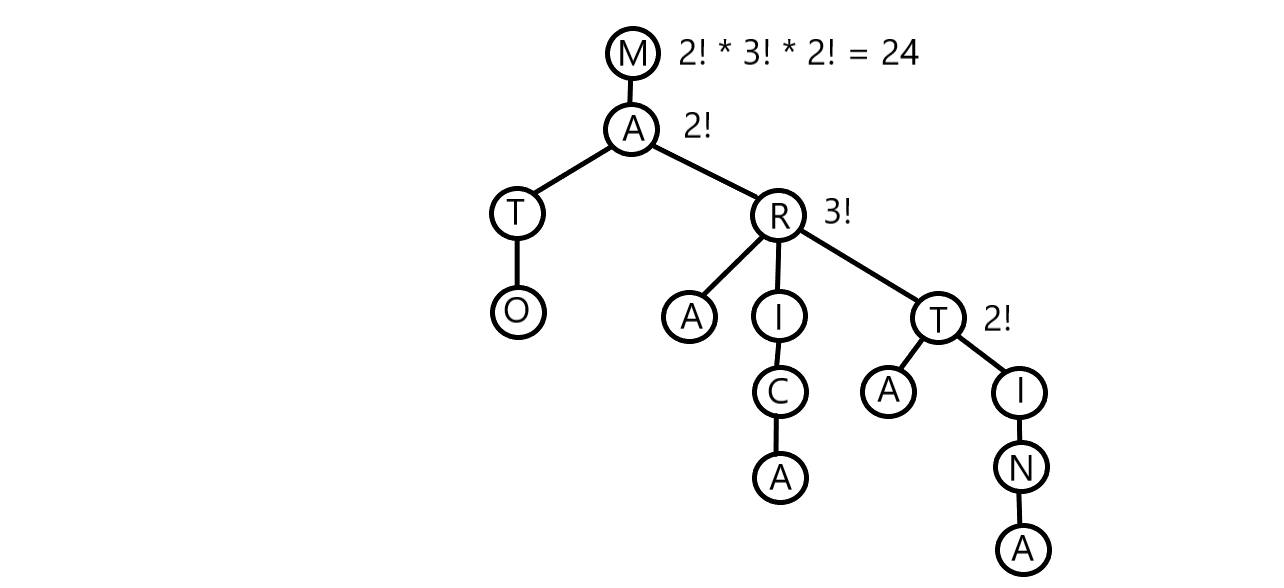
저번 문제가 조합을 구하는 문제였다면, 이번 문제는 순열을 구하는 것이 차이입니다. 조합은 합의 관계와 곱의 관계 간 연산 순서가 바뀌어서는 안 되었기 때문에 DFS로 구했지만, 이번 문제에선 부모 자식 관계에 상관 없이 어떤 순서로든 각 노드의 차수 \(D\)에 대하여 \(\prod_{i=1}^{||S||}D_i!\), 즉 팩토리얼들의 곱을 구하면 됩니다. 이렇게만 놓고 보면 참 쉬운 문제같은데, 사실 복병은 다른 곳에 숨어있습니다.
Trie 자료구조의 한계
트라이는 여러 문자열을 저장하고 효율적으로 검색할 수 있는 자료구조입니다. 검색 대상이 되는 문자열 풀의 크기와는 상관없이, 검색하려는 문자열 길이만큼만 트라이를 타고 들어가면 답이 나온다는 점에서 매우 빠르게 쿼리를 처리할 수 있습니다. 시간복잡도에 있어서는 매우 강력한 자료구조임은 부정할 수 없습니다.
하지만 공간으로 넘어가면 얘기가 달라집니다. 각 노드가 한 글자를 나타내는 일반적인 트라이에는 문자열 풀의 길이 총 합 \(||S|| = \sum_{i=1}^N |S|\)에 비례하는 개수의 노드가 들어있습니다. 거기다 각 노드는 자식 노드로 향하는 모든 포인터를 갖고 있어야 합니다. 보통 알파벳 대문자 혹은 소문자로만 이루어진 문자열들을 처리한다고 해도 26개의 포인터 배열을 위한 메모리가 할당되어 있어야 한다는 뜻이 됩니다. 이번 문제에서 기대되는 메모리 크기를 대충 계산해봅시다. 문자열 \(3000\)개의 각 길이는 최대 \(3000\)이고, 각 노드가 길이 \(26\)인 포인터 배열을 갖는다고 할 때 \(3000 \times 3000 \times 26\)인데, 2억 언저리가 나옵니다. 포인터는 기본 4바이트, 환경에 따라 8바이트까지 될 수 있음을 생각하면 끔찍한 크기입니다. 물론 노드 수가 정말로 \(N^2\)이 될 일은 없겠지만 손을 쓰긴 해야 합니다. 이를 줄여보고자 HashMap을 쓸 수도 있지만, 고작 26개의 포인터를 아껴보려고 비싼 자료구조를 억지로 집어넣는다 한들 메모리는 크게 줄지 않습니다. 비트필드로 이 문제를 해결하는 방법도 있지만, 노드의 수 자체를 줄이지 않고는 드라마틱한 결과를 기대하기는 어렵습니다. 이대로는 희망이 없는데요…
Compact Trie
만약 트라이에서 가지를 뻗지 않는 구간은 하나의 단위로 합쳐준다면 어떨까요. 그렇다면 문자열 길이에 비례하여 노드의 수가 늘어나지는 않을 겁니다. 이런 아이디어에서 나온 것이 압축 트라이입니다. 영어로는 Compact trie, Compressed trie, Radix trie 등으로 불리는 녀석인데 트라이의 고질적 문제인 메모리 비효율성을 해결하기 위해 특정 구간을 하나의 노드가 갖고 있게 합니다.
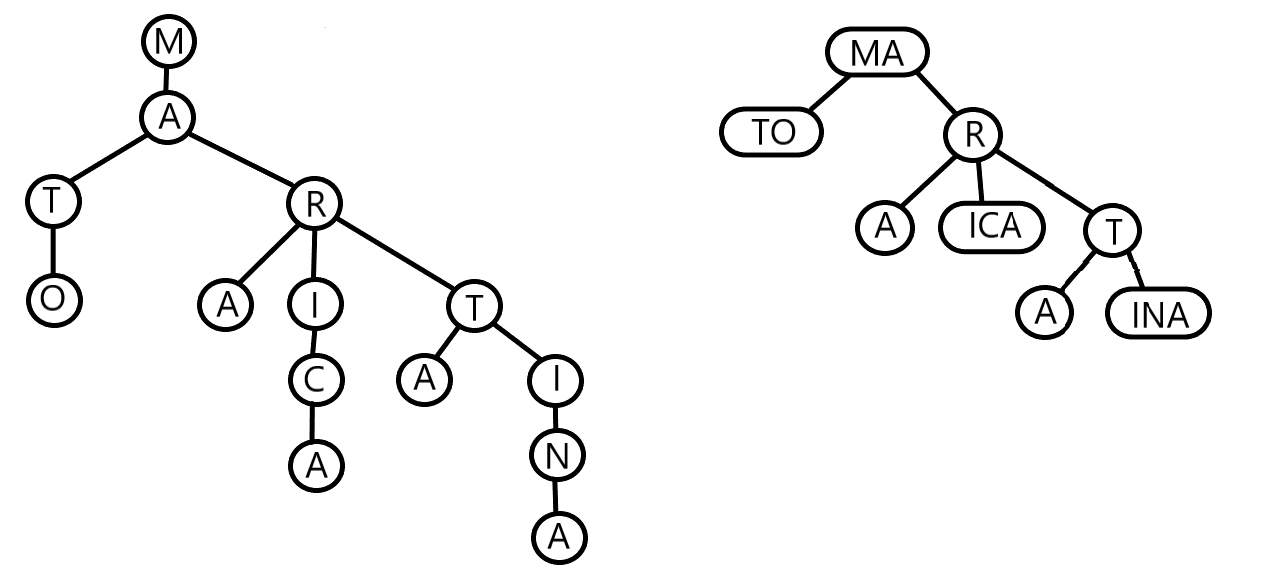
이렇게 되면 트라이에 존재할 수 있는 노드의 수는 많아야 \(2N\)개가 됨을 보장할 수 있습니다. 만약 어떤 문자열을 집어넣을 때 루트에 바로 붙거나 구간을 가르지 않는다면 노드 하나만 추가됩니다. 구간을 갈라 분기를 만든다면 노드 두 개가 추가됩니다.
압축 트라이의 구현은 이 글을 참고했습니다.
#include <iostream>
#include <cstring>
typedef long long ll;
const int LEN = 3001;
const int ALPHABET = 26;
const ll MOD = 1e9 + 7;
char s[LEN][LEN];
int N, s_len[LEN]; // 문자열 길이 배열
ll fact[LEN] = { 1, 1, }; // 메모이제이션
class Trie { // radix trie
struct Node {
Node* go[ALPHABET];
int degree, idx, match_count;
Node() : degree(0), idx(-1), match_count(0) { for (int i = 0; i < ALPHABET; ++i) go[i] = 0; }
~Node() { for (int i = 0; i < ALPHABET; ++i) if (go[i]) delete go[i]; }
void insert(int id, int pos) {
if (s_len[id] == pos) {
++degree; // 문자열의 끝일 때에도 차수 1 증가
return;
}
int next = s[id][pos] - 'A';
if (!go[next]) {
++degree; // 분기가 늘어나면 차수 1 증가
Node* n = new Node;
n->idx = id;
n->match_count = s_len[id] - pos; // 분기에서 갈라진 새 노드가 가지는 구간 길이
go[next] = n;
}
else {
int i, n_id = go[next]->idx;
bool full_match = true; // 구간을 모두 포함하는가?
for (i = 0; i < go[next]->match_count; ++i) {
if (s_len[id] == pos + i || s[id][pos + i] != s[n_id][pos + i]) { // 다르다면
full_match = false; // 구간이 갈라져야 합니다
break;
}
}
if (!full_match) {
Node* n = new Node;
n->idx = id;
n->match_count = i;
go[next]->match_count -= i;
int branch = s[n_id][pos + i] - 'A';
n->go[branch] = go[next];
n->degree = 1;
go[next] = n;
}
}
go[next]->insert(id, pos + go[next]->match_count);
}
ll dfs() {
ll result = fact[degree];
for (int i = 0; i < ALPHABET; ++i) {
if (go[i]) {
result *= go[i]->dfs();
result %= MOD;
}
}
return result;
}
} *root;
public:
Trie() { root = new Node; }
~Trie() { delete root; }
void insert(int id) { root->insert(id, 0); }
ll dfs() { return root->dfs(); }
} trie;
int main() {
for (int i = 2; i < 30; ++i)
fact[i] = fact[i - 1] * i % MOD;
std::cin >> N;
for (int i = 0; i < N; ++i) {
std::cin >> s[i];
s_len[i] = strlen(s[i]);
trie.insert(i);
}
std::cout << trie.dfs();
}
문자열 검색 등의 과정 없이, 단지 트리의 위상만 필요한 경우라면 메모리 뿐 아니라 시간도 단축되는 효과를 볼 수 있습니다. 실제로 Prefix-free subsets도 압축 트라이로 풀었더니 시간이 조금 더 개선되는 걸 확인했습니다.
여담으로 Prefix-free subsets 문제에 기여하면서 난이도를 골드 1로 매겼는데, 비슷한 컨셉으로 해결해야 하는 이번 문제는 플래 3인 걸 고려하면 너무 짜게 준 게 아닌가 싶네요.