아무도 못 푼 문제 - Prefix Free Subsets

아무도 못 푼 문제 시리즈가 돌아왔습니다. 이번에 볼 문제는 바로 Prefix Free Subsets입니다. 아무도 못 푼 문제들이 다 그렇듯 이 문제 또한 영어로 되어있으니, 간단히 옮겨보죠.

Prefix-free set은 문자열들의 집합으로, 그 어떠한 문자열도 다른 문자열의 접두사가 아닌 것을 가리킵니다. 예를 들어 공집합, {hello, hi}는 Prefix-free입니다. 반면에 {hello, hell}은 그렇지 않습니다. 어떤 문자열들의 집합이 주어졌을 때, 그 집합의 부분집합 중 Prefix-free인 것들의 개수를 모두 찾으면 됩니다. 전체집합과 공집합도 개수에 포함됩니다.

주어지는 집합의 크기 \(N\)은 \(1\) 이상 \(62\) 이하입니다.

\(N\)이 최대 \(62\)니까 가능한 모든 부분집합의 개수는 \(2^{62}\)입니다. 이 말인 즉슨, 집합을 하나하나 다 구해서 풀어서는 답도 없다는 겁니다. 집합 개수만 따져도 \(O(2^N)\)인데, 실제로는 각 부분집합의 모든 원소들이 접두사 관계인지를 확인해야 하므로 실제로 시간은 더 소모될 수 밖에 없습니다. 뭔가 다른 방법은 없을까요?

접두사, 여러 문자열. 이런 키워드를 보고 있으니 하나 떠오르는 구조가 있습니다. 바로 트라이 Trie입니다. 트라이의 다른 이름이 접두사 트리(Prefix tree)이기도 하죠. 트라이의 형태에 어떤 연산을 하면, 문제에서 요구하는 집합의 개수를 구할 수 있지 않을까요.

천천히 생각해봅시다. 집합 {ab, ac}가 있을 때, Prefix-free인 것은 \(\varnothing\), {ab}, {ac}, {ab, ac}가 있습니다. 개수는 4개입니다. 한 개의 원소에 대해서만 생각해보자면 어떤 부분집합에 그 원소는 들어가거나, 들어가지 않거나 둘 중 하나일 겁니다. 그리고 두 원소가 각각 접두사 관계가 아니라면-독립이라면-곱의 관계가 성립할 겁니다. 이걸 트라이 구조와 연관지어 생각해보면 다음처럼 생각해볼 수 있습니다.

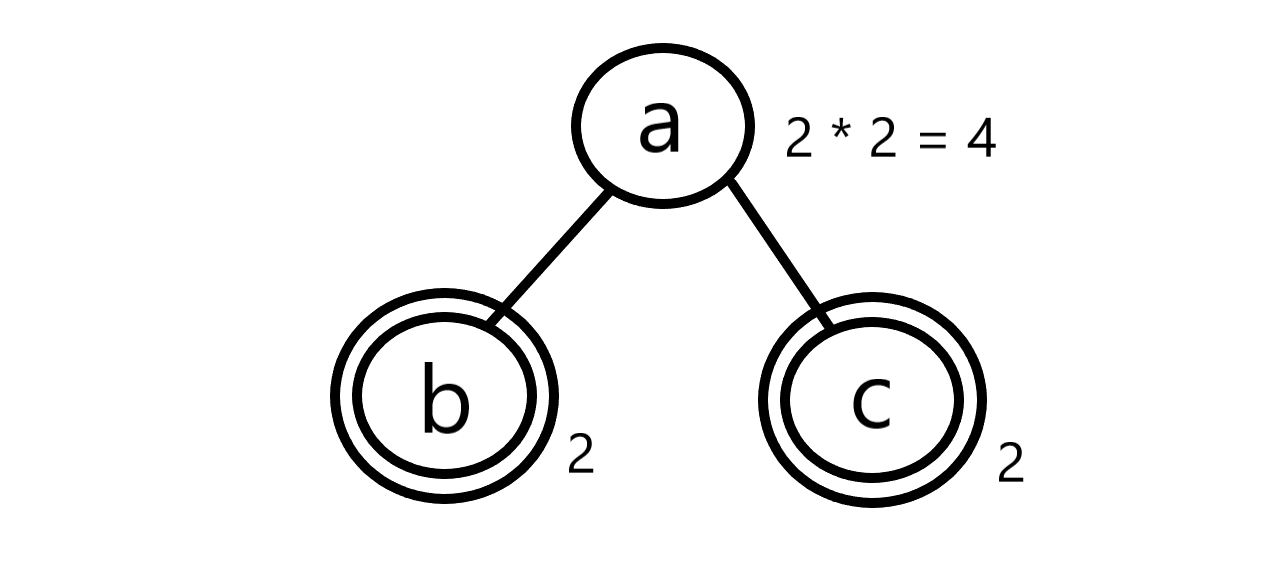
result

트라이의 어떤 노드의 자식들이 갖는 경우의 수는 모두 곱해주는 겁니다. 위 예시에서는 \(2 \times 2 = 4\)가 됩니다.

이제 조금 복잡한 경우도 생각해볼 수 있습니다. 집합 {a, ab, ac}의 Prefix-free를 모두 구하면 어떻게 될까요? a를 고른 시점에 다른 원소들은 더이상 고를 수 없게 됩니다. a는 다른 원소들의 접두사이기 때문에-종속이라서-ab, ac로 구성할 수 있는 부분집합들과는 합의 관계가 성립합니다. \(\varnothing\), {a}, {ab}, {ac}, {ab, ac} 5개가 있겠네요. 이걸 그림으로 나타내면 다음과 같습니다.

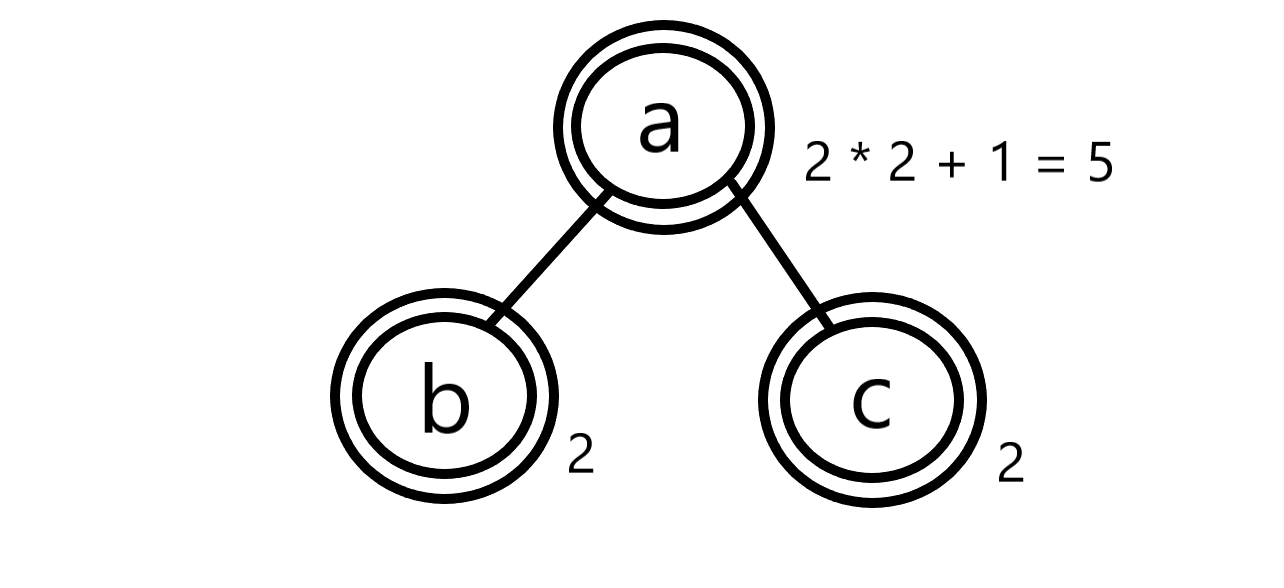
result

트라이에서 부모 노드는 자식 노드들의 접두사를 의미합니다. 부모 노드를 부분집합에 넣은 순간, 자식 노드들은 어떤 식으로든 선택할 수 없게 됩니다. 달리 말해서, 모든 자식 노드들 간의 경우의 수를 다 구한 것과 별개로 부모 노드만을 선택하는 하나의 경우가 따로 생기게 되므로, 1을 더해주게 됩니다.

상당히 복잡한 집합에 대해서도 이러한 계산은 유효합니다.

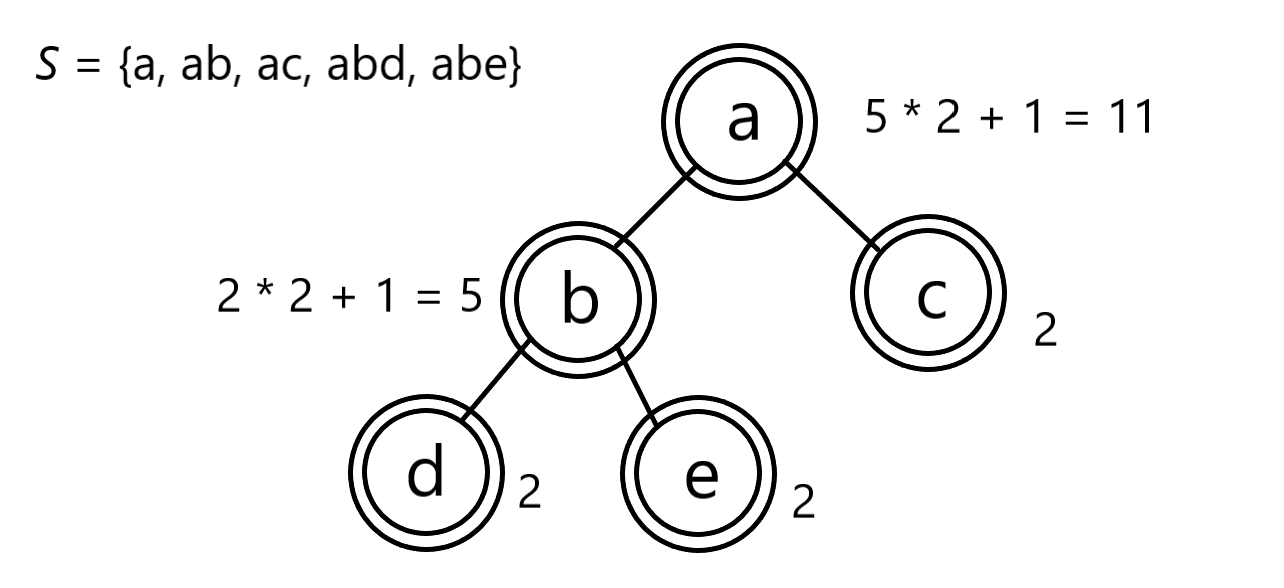
result

실제로 위 예시에서 Prefix-free subsets를 구해보면 \(\varnothing\), {a}, {ab}, {ac}, {abd}, {abe}, {ab, ac}, {abd, abe}, {abd, ac}, {abe, ac}, {abd, abe, ac}로 11개 있음을 확인할 수 있습니다.

예제들도 마찬가지 방식으로 풀 수 있습니다.

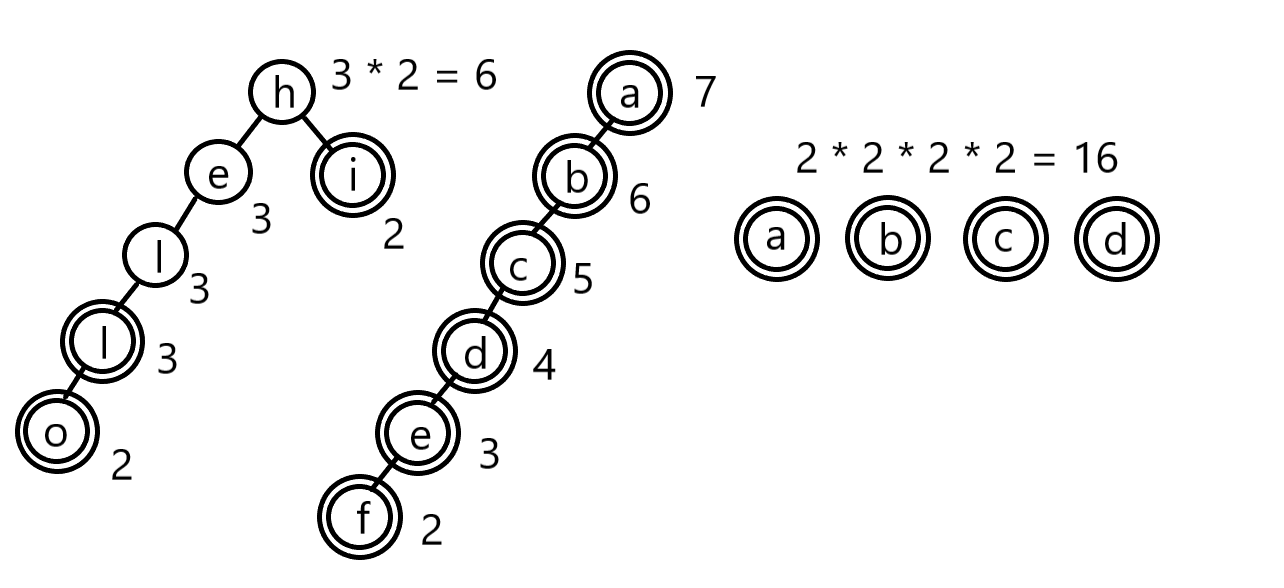
result

꽤 잘 들어맞는군요.

이제 알고리즘을 일반화해봅시다.

자식들이 갖는 경우의 수는 모두 곱합니다.
부모 노드가 갖는 경우의 수는 합합니다.

리프 노드들로부터 계산된 결과는 최종적으로 루트 노드로 모여야 합니다. dfs로 모든 노드를 한 번씩만 방문하여 모든 경우의 수를 계산할 수 있게 됩니다. 트라이에서의 노드의 수 \(|V|\)는 최악일 때 모든 문자열들의 길이의 합 \(\sum|S|\)가 됩니다. 모든 문자열들은 길이가 \(100\)을 넘지 않으므로, 노드의 수가 아무리 많더라도 \(6200\)개인 것이죠. 시간복잡도는 이제 \(O(2^{62})\)에서 \(O(6200)\)이 되는… 거의 기적에 가까운 일이 일어납니다.

그럼 문제를 풀어봅시다.

#include <iostream>
#include <map>

typedef long long int ll;
class Trie { // 트라이 자료구조
private:
	struct Node {
	public:
		std::map<char, Node*> go; // 트라이는 메모리 초과가 일어나기 쉬우니 주의
		int output;
		Node() : output(0) { }
		~Node() { for (auto [k, n] : go) delete n; }
		void insert(std::string s, int i) {
			if (i == s.length()) {
				output += 1; // 문자열의 끝임을 표시합니다.
				return;
			}
			char next = s[i];
			if (go.find(next) == go.end()) go[next] = new Node;
			go[next]->insert(s, i + 1);
		}
		ll dfs() const { // 집합의 개수를 구하기 위해 정의된 dfs
			ll result = 1;
			for (const auto& [k, n] : go) result *= n->dfs(); // 자식 노드들의 경우의 수는 모두 곱합니다.
			return result + output; // 부모 노드의 경우의 수는 합합니다. (리프 노드는 자동적으로 2를 반환)
		}
	};
	Node* root;
public:
	Trie() { root = new Node; }
	~Trie() { delete root; }
	void insert(std::string s) { root->insert(s, 0); }
	ll get_count() const { return root->dfs(); }
};

int main() {
	int T;
	std::cin >> T;
	for (int i = 1; i <= T; ++i) {
		Trie t; 
		int N;
		std::string s;
		std::cin >> N;
		while (N--) {
			std::cin >> s;
			t.insert(s);
		}
		std::cout << "Case #" << i << ": " << t.get_count() << '\n';
	}
}

사실 꽤 엄밀하게 풀었다 생각하고 제출했는데 WA를 받아서 썩 기분이 좋진 않았습니다. 그런데 몇 시간 뒤에 데이터가 잘못된 것 같다는 요청글이 올라와서, 이건 좀 기다려봐야 하지 않을까 싶습니다. 작업 공정 문제도 데이터가 잘못된 것이 아닐까, 하는 강한 심증은 있지만 어떻게 증명할 방법은 없으니 누군가 해결할 때까지 기다려봐야겠습니다.

2023년 2월 4일 재채점되면서 정답 처리 되었습니다. 이렇게 백준의 문제 하나가 해결되었네요.

Categories