성균관대학교 프로그래밍 경진대회 Open Contest 2023
SSAFY도 이제 2개월을 넘겼고, 슬슬 역량평가를 쳐야 합니다. IM형만 붙으면 이수 조건은 충족하지만 A형, 넘어서는 B형도 따보고 싶군요. 시험 대비나 할 겸 성균관대학교 프로그래밍 경진 대회에 참가했습니다. 성적은 초라하지만, 일단 풀어본 문제를 복기해보겠습니다.
A. 증가 배열 만들기
첫 문제부터 만만치 않습니다. 보통 A번은 단순 구현 문제가 나오는데, 그래도 이건 조건을 만족하는지 확인하는 절차가 하나 들어갑니다. 조건이라고 해봐야 \(K >= N + M - 1\)인지만 확인하면 되긴 합니다. 조건을 만족한다면 배열 만들기는 어렵지 않습니다.
B. 토크나이저
단순 문자열 처리 문제.
C. 마법박스
갑자기 난이도가 수직상승하는 구간. 쿼리 수를 줄이기 위해 매개변수탐색을 해야겠다는 건 알겠습니다. 그런데 \(N \le 5,000,000 \)이고, \(\log 5,000,000 \approx 22 \)이므로 최악의 경우엔 쿼리 수 제한 \(20\)을 넘겨버리게 됩니다.
하지만 문제의 조건에서 어떤 수가 들어가면, 그의 배수는 모두 포함한다고 합니다. 그렇다면 포함되지 않는 숫자 중 가장 작은 것은 무조건 소수가 됨을 알 수 있고, 매개변수탐색의 대상이 되는 집합을 소수로 줄일 수 있습니다. \(N\) 이하인 소수의 개수는 \(400,000\)을 넘기지 않고, \(\log 400,000 \approx 19 \)이므로 아슬아슬하게 통과가 가능합니다.
D. 벌레컷
누적합 + 이분탐색.
우선 배열 \(S_i = \sum A_i\)를 정의합니다.
\(1\)부터 \(N - 2\)까지의 모든 \(X\)에 대해,
- \(S_X \le S_N - S_Y\)인 \(Y\)를 찾아줍니다.
- \(S_M - S_X \ge S_N - S_M\)인 \(M\)을 찾아줍니다.
모든 \(X\)에 대해 \(Y-M+1\)을 다 더해주면 됩니다.
E. AB
해싱으로 풀 수도 있고, 트라이로 풀 수도 있는 문제. 저는 트라이로 풀었습니다. 메모리 초과가 나지 않은 걸로 봐서는 테스트 케이스는 그리 빡빡하지 않은 것 같습니다.
F. 최소 트리 분할
그들만의 리그가 시작되는 구간… 사실 처음엔 저도 그냥 넘어갔습니다만, 다시 잘 생각해보니 그냥 트리 순회 문제였네요. 다음과 같이 생각해볼 수 있습니다. 어떤 한 점에서 뻗어나가면서 목표 가중치가 더 작아진다면, 트리는 분할할 필요가 없습니다. 하지만 목표 가중치가 더 커진다면, 이 때는 트리가 분할되어야 합니다.
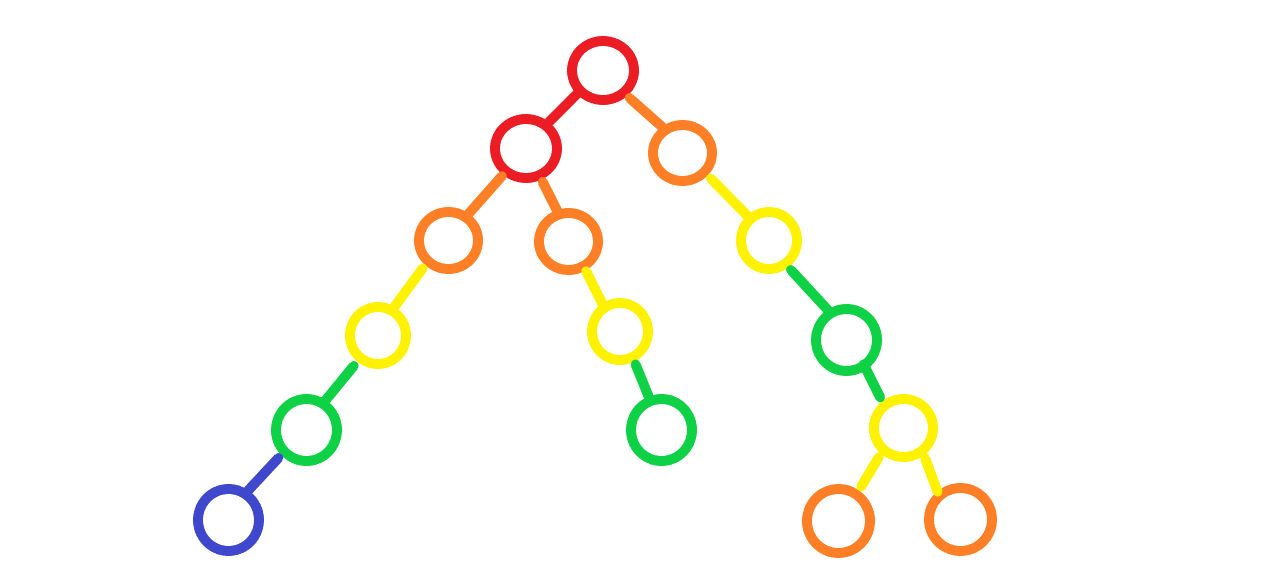
좀 그려지시나요? 빨간색에 가까울수록 가중치가 커진다고 해봅시다. 그림을 그려보니 트리가 어디까지 한꺼번에 갱신되어야 하는지 보이는군요. DFS나 BFS로 풀 수 있겠습니다.
#include <iostream>
#include <vector>
#include <queue>
typedef long long int ll;
const int LEN = 100'001;
std::vector<int> graph[LEN];
bool visited[LEN];
int N, u, v, A[LEN];
ll bfs() {
ll result = A[1];
std::queue<int> q;
q.push(1);
visited[1] = true;
while (q.size()) {
int u = q.front(); q.pop();
for (const int v : graph[u]) {
if (visited[v]) continue;
if (A[v] > A[u]) // 가중치가 더 커지는 경우에만
result += A[v] - A[u]; // 트리를 분할합니다.
visited[v] = true;
q.push(v);
}
}
return result;
}
int main() {
std::cin >> N;
for (int i = 1; i <= N; ++i) std::cin >> A[i];
for (int i = 1; i < N; ++i) {
std::cin >> u >> v;
graph[u].push_back(v);
graph[v].push_back(u);
}
std::cout << bfs();
}
다른 분들의 코드를 참고해보니 풀이는 대략 두 가지로 나뉩니다. 저처럼 순회로 푼 분들도 있고, 유니온 파인드로 푼 사람들도 있습니다. 다만 순회로 푼 쪽이 성능상 약간 더 빠른 경향이 있습니다.
G. 시험
못 풀었습니다.
H. 점프
사실상 마지막 문제. 이 다음부터는 푼 사람이 거의 없습니다.
느리게 갱신되는 세그먼트 트리 문제를 하나라도 풀어보았다면, 의외로 쉽게 접근할 수 있는 문제입니다. 저는 다행히도 Circuits를 먼저 풀어보면서 이 문제에 접근하는 관점을 금방 찾을 수 있었죠. \(K = 1\)일 때부터 닿을 수 있는 모든 좌표에 대해 최소값을 갱신해나가면 됩니다.
발판의 너비만큼의 구간에 대한 최소값을 찾고, 또한 그 너비 구간만큼 최소값을 갱신해야 하므로, Circuits에서 썼던 바로 그 세그먼트 트리를 약간만 고쳐서 그대로 가져다 쓸 수 있겠습니다.
#include <iostream>
#include <vector>
#include <algorithm>
const int INF = 1e9;
const int LEN = 300'001;
struct Edge {
int l, r, k, i, j;
bool operator<(const Edge& rhs) const { return k < rhs.k; }
};
std::vector<int> posY;
std::vector<Edge> v;
int N, K, L, R, Ki;
int seg_min[LEN * 7], lazy[LEN * 7]; // 최소값 세그먼트 트리
void propagate(int s, int e, int i) { // lazy propagation
if (~lazy[i]) {
seg_min[i] = lazy[i];
if (s ^ e) {
lazy[i << 1] = lazy[i];
lazy[i << 1 | 1] = lazy[i];
}
lazy[i] = -1;
}
}
void update_diff(int l, int r, int d, int s = 0, int e = posY.size() - 1, int i = 1) {
propagate(s, e, i);
if (e < l || r < s) return;
if (l <= s && e <= r) {
seg_min[i] = d;
if (s ^ e) {
lazy[i << 1] = d;
lazy[i << 1 | 1] = d;
}
return;
}
int m = s + e >> 1;
update_diff(l, r, d, s, m, i << 1);
update_diff(l, r, d, m + 1, e, i << 1 | 1);
seg_min[i] = std::min(seg_min[i << 1], seg_min[i << 1 | 1]);
}
int get_min(int l, int r, int s = 0, int e = posY.size() - 1, int i = 1) {
propagate(s, e, i);
if (e < l || r < s) return INF;
if (l <= s && e <= r) return seg_min[i];
int m = s + e >> 1;
return std::min(get_min(l, r, s, m, i << 1), get_min(l, r, m + 1, e, i << 1 | 1));
}
int main() {
std::cin >> N >> K;
for (int i = 0; i < LEN * 7; ++i) seg_min[i] = INF, lazy[i] = -1;
for (int i = 0; i < N; ++i) {
std::cin >> L >> R >> Ki;
posY.push_back(L); posY.push_back(R);
v.push_back({ L, R, Ki });
}
// 좌표를 압축해줍니다.
std::sort(posY.begin(), posY.end());
posY.erase(std::unique(posY.begin(), posY.end()), posY.end());
for (Edge& e : v) {
e.i = std::lower_bound(posY.begin(), posY.end(), e.l) - posY.begin();
e.j = std::lower_bound(posY.begin(), posY.end(), e.r) - posY.begin();
e.j -= 1;
}
std::sort(v.begin(), v.end());
// K = 1일 때를 먼저 처리해줍니다.
int ptr = 0, min;
while (ptr < v.size() && v[ptr].k == 1) {
update_diff(v[ptr].i, v[ptr].j, 0);
++ptr;
}
// K - 1까지의 높이에 대해, 닿을 수 있는 구간의 최소값을 처리합니다.
for (int k = 2; k < K; ++k) {
while (ptr < v.size() && v[ptr].k == k) {
min = get_min(v[ptr].i, v[ptr].j);
if (min < INF) // 닿을 수 있는 구간이라면
update_diff(v[ptr].i, v[ptr].j, min + 1); // 점프 횟수 1 추가
++ptr;
}
}
// 높이 K일 때, 최소값을 구하거나 닿을 수는 있는지 확인합니다.
min = -1;
while (ptr < v.size() && v[ptr].k == K) {
Ki = get_min(v[ptr].i, v[ptr].j) + 1;
if (Ki < INF) { // 닿을 수 있다면
if (!~min || Ki < min) min = Ki; // 최소값을 갱신합니다.
}
++ptr;
}
if (K == 1) min = 0; // 예외 처리 주의...
std::cout << min;
}
나머지 문제들은 손도 못 댔습니다. 나중에 풀어봐야겠네요.