백준 16357 - Circuits
아직 싸피는 초반이라 그런지 여유가 있네요. 하지만 그렇다고 맘놓고 놀 생각은 없습니다. 이번에 짚어볼 문제는 Circuits입니다. 단계별로 풀어보기도 거의 마지막에 다다르니, 사람들이 거의 손도 대지 않은 문제들 뿐입니다.
문제는 생각보다 단순합니다. 원문이 영어니까, 적당히 옮겨보겠습니다.
하나의 칩 위에 여러 개의 회로를 여러 층으로 쌓아 올립니다. 설계 상의 한계 때문에, 회로와 연결할 배선은 가로로 수평이 되도록 두 줄만 배치할 수 있습니다. 모든 회로들은 축과 평행한 직사각형의 형태로 주어집니다. 가장 많은 회로를 연결할 수 있도록 선을 배치하고, 그 때의 연결된 회로의 최대 개수를 찾아주세요.
저번에 풀어봤던 Egg처럼, 스위핑으로 풀 수 있겠습니다. 여러 범위들이 주어지고 이를 계속 갱신해가며 어떤 값을 찾을 수 있겠죠. 대신 좌표 값이 매우 크기 때문에 좌표 압축은 해야겠습니다. 그런데 무엇을 어떻게 갱신해야 하는 걸까요? 사실 처음에 생각해본 건 일단 모든 회로를 다 얹어놓고, 가장 많이 겹치는 부분을 기준으로 두 번째로 큰 값과 더해보면 어떻까 싶었습니다. 하지만 이렇게 그리디하게 접근해서는 제대로 답을 찾을 수 없으니, 다른 방법을 생각해내야 했습니다.
어떤 한 점을 고정하고 그와 겹치지 않는 다른 모든 구간들을 업데이트하는 식으로 최대값을 찾을 수 있긴 합니다. 이렇게 되면 영역의 모든 점을 한 번씩 고정한다고 할 때, 모든 영역을 훑게 되고, 또 매번 구간을 업데이트하므로 기대되는 시간복잡도는 \(O(N^2\log N)\)입니다. 어림도 없죠.
하지만 한 점을 고정한다고 할 때, 다른 모든 구간을 업데이트할 필요가 있는지 다시 생각해볼 필요가 있습니다. 점 \(p1\)을 지금 고정한 점이라고 해봅시다. 구간을 왼쪽에서 오른쪽으로 스위핑하며 훑고 지나간다고 할 때, \(p1\)의 왼쪽은 구간 업데이트가 모두 완료되어 있으므로, 최대값 \(p2\)를 찾을 수 있습니다. 하지만 구간의 오른쪽은 찾을 수가 없는데요.
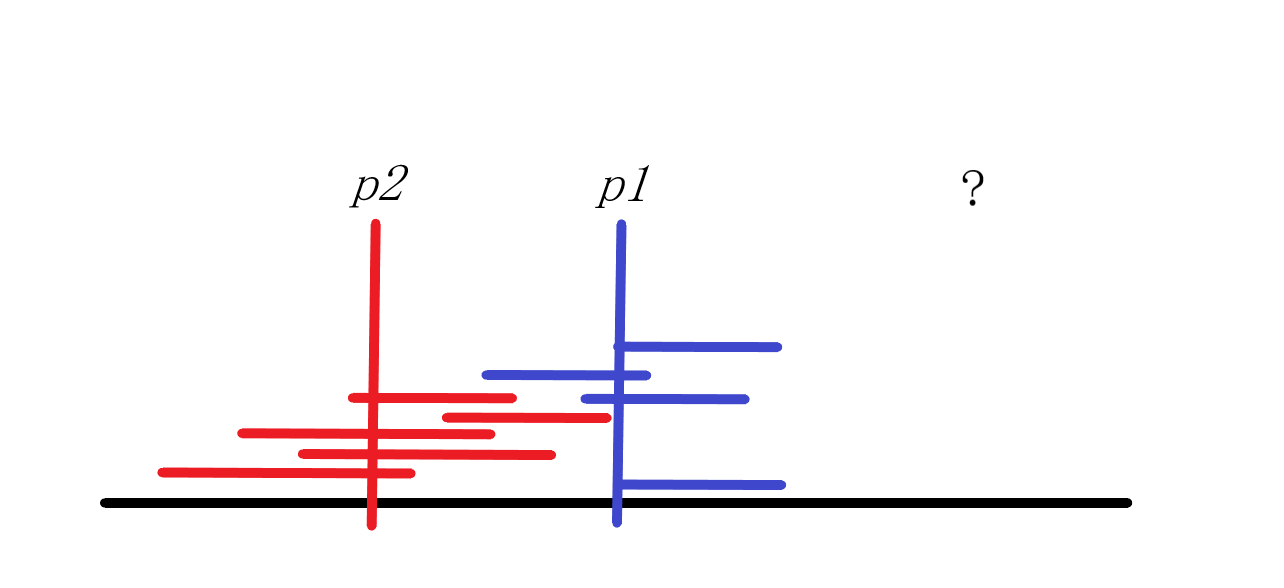
그림의 빨간 구간들은 모두 업데이트가 완료되었습니다. 파란 구간들은 \(p1\)에 걸쳐 있습니다. \(p1\)과 \(p2\)의 합이 최대가 될 때의 그 값을 구하면 된다는 건 알겠는데, 오른쪽의 \(p2\)는 어떻게 찾을까요? 사실 굳이 찾을 필요 없습니다.
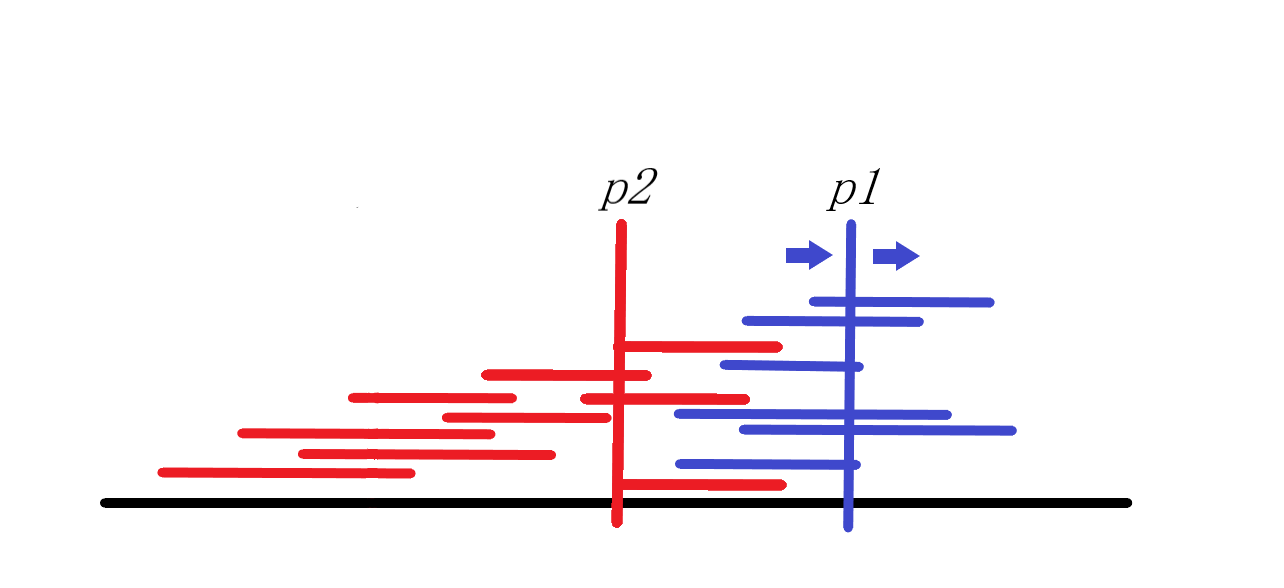
결국 \(p1\)이었던 지점은 나중에 \(p2\)의 구간에 포함되므로, 우리는 그저 좌표값이 커지는 순서대로 업데이트만 해주다보면 모든 순서쌍을 고려할 수 있게 됩니다. 이제 한 점을 고정했을 때 모든 구간을 업데이트할 필요가 없으므로 시간복잡도는 \(O(N\log N)\)가 됩니다.
저번에 풀어봤던 세그먼트 트리 문제와는 달리, 이번 문제는 Lazy propagation을 적용해야 합니다. 넒은 구간 업데이트가 자주 발생하고, 또한 넓은 구간들에서 최대값을 빠르게 찾을 수 있어야 합니다. 이 때, 넓은 구간을 하나하나 업데이트하게 되면 최악일 때 \(O(N\log N)\)이므로 보통의 세그먼트 트리로는 제한된 시간 내에 해결이 불가능합니다. 이 글을 보면 아시겠지만 넓은 구간을 업데이트하고, 또 넓은 구간에 대한 값을 구해야 할 때, Lazy propagation은 제법 괜찮은 솔루션이 될 수 있다는 걸 쉽게 이해하실 수 있습니다.
그럼 문제를 풀어봅시다.
#include <iostream>
#include <vector>
#include <algorithm>
typedef long long int ll;
const int MAX = 200'000;
struct Vertex { int y, y1, y2, q; }; // 쿼리의 기준이 되는 y좌표, y1 - y2 구간, 쿼리의 종류
bool CompY(const Vertex& a, const Vertex& b) { return a.y < b.y; }
std::vector<int> posY;
std::vector<Vertex> v;
int N, ux, uy, vx, vy;
ll segTree[MAX * 4];
ll lazy[MAX * 4];
void propagate(int index, int start, int end) { // lazy propagation
if (lazy[index]) {
segTree[index] += lazy[index];
if (start != end) {
lazy[index * 2] += lazy[index];
lazy[index * 2 + 1] += lazy[index];
}
lazy[index] = 0;
}
}
void update_diff(int left, int right, ll diff, int index = 1, int start = 0, int end = posY.size() - 1) {
propagate(index, start, end);
if (left > end || right < start) return;
if (left <= start && end <= right) {
segTree[index] += diff;
if (start != end) {
lazy[index * 2] += diff;
lazy[index * 2 + 1] += diff;
}
return;
}
int mid = (start + end) / 2;
update_diff(left, right, diff, index * 2, start, mid);
update_diff(left, right, diff, index * 2 + 1, mid + 1, end);
segTree[index] = std::max(segTree[index * 2], segTree[index * 2 + 1]); // 최대값을 저장합니다.
}
ll get_max(int left, int right, int start = 0, int end = posY.size() - 1, int index = 1) {
propagate(index, start, end);
if (left > end || right < start) return 0;
if (left <= start && end <= right) return segTree[index];
int mid = (start + end) / 2;
return std::max(get_max(left, right, start, mid, index * 2), get_max(left, right, mid + 1, end, index * 2 + 1));
}
int main() {
std::cin >> N;
for (int i = 0; i < N; ++i) {
std::cin >> ux >> uy >> vx >> vy; // x 좌표는 받을 필요 없습니다.
posY.push_back(uy); posY.push_back(vy);
v.push_back({ vy, vy, uy, 1 }); // vy -> uy 방향으로 훑습니다. p1 추가 쿼리는 1입니다.
v.push_back({ uy, vy, uy, 0 }); // p2 추가 쿼리는 0입니다.
}
// 좌표 압축
std::sort(posY.begin(), posY.end());
posY.erase(std::unique(posY.begin(), posY.end()), posY.end());
for (Vertex& e : v) {
// 쿼리 1일 때는 기준 y만 압축합니다.
if (e.q) e.y = std::lower_bound(posY.begin(), posY.end(), e.y) - posY.begin();
else { // 쿼리 0일 때는 구간 좌표도 모두 압축해야 합니다.
int y1 = std::lower_bound(posY.begin(), posY.end(), e.y1) - posY.begin(),
y2 = std::lower_bound(posY.begin(), posY.end(), e.y2) - posY.begin();
e.y = y2 + 1, e.y1 = y1, e.y2 = y2; // 실제 p2 추가 쿼리는 y2 + 1 시점에서 이루어져야 합니다.
}
}
std::sort(v.begin(), v.end(), CompY);
// 쿼리 수행
ll p1 = 0, p2, max = 0;
for (int i = 0, j = 0; i < posY.size(); ++i) {
while (j < v.size() && v[j].y == i) {
if (v[j].q) ++p1; // 쿼리가 1이라면, p1에 걸치게 됩니다.
else --p1, update_diff(v[j].y1, v[j].y2, 1); // 쿼리 0일 때, p1에서는 벗어나고, p2에 추가됩니다.
++j;
}
p2 = get_max(0, i - 1);
max = std::max(max, p1 + p2); // 최대값을 구합니다.
}
std::cout << max;
}개인적인 생각으로는, 어지간하면 좀 어려워보인다 싶은 문제도 Segment tree로 풀 수 있고, 그 이상의 개념을 적용해야만 하는 경우는 극히 제한적인 것이 아닌가 합니다. 넓은 구간을 업데이트하고, 한 지점에 대한 조회를 처리한다면 이는 그냥 세그먼트 트리로 해결 가능합니다. 한 지점을 업데이트하고 넓은 구간을 조회한다면, 이것도 그냥 세그먼트 트리를 쓰면 되죠. 반드시 Lazy propagation을 써야 한다면, 이는 즉 업데이트 구간이 넓고 또한 조회 구간도 넓어야 하는 거죠. 어디까지나 혼자 생각하는 거라 정답은 아니겠지만, 적어도 지금은 그렇게 느껴집니다. 마찬가지로 persistent segment tree를 써야만 하는 경우도 생각해볼 수 있겠지만, 아직 거기까진 손을 대지 않았으니 여기까지만 하겠습니다.