이번에 풀어본 문제는 기하학 지식을 십분 활용해야 하는 삼각형입니다.

이 문제는 잘 생각해보면 결국 제한된 각도 내에서 특정 선분보다 아래에 있는 점이 있는지를 판단하는 방법에 대한 것이 됩니다. 만일 각도 구간이 전체라면, 임의의 직선보다 원점에 더 가까운 점을 찾는 문제가 되겠죠. 문제는 각도가 정해진 상태에서 이걸 빠르게 처리하는 겁니다.

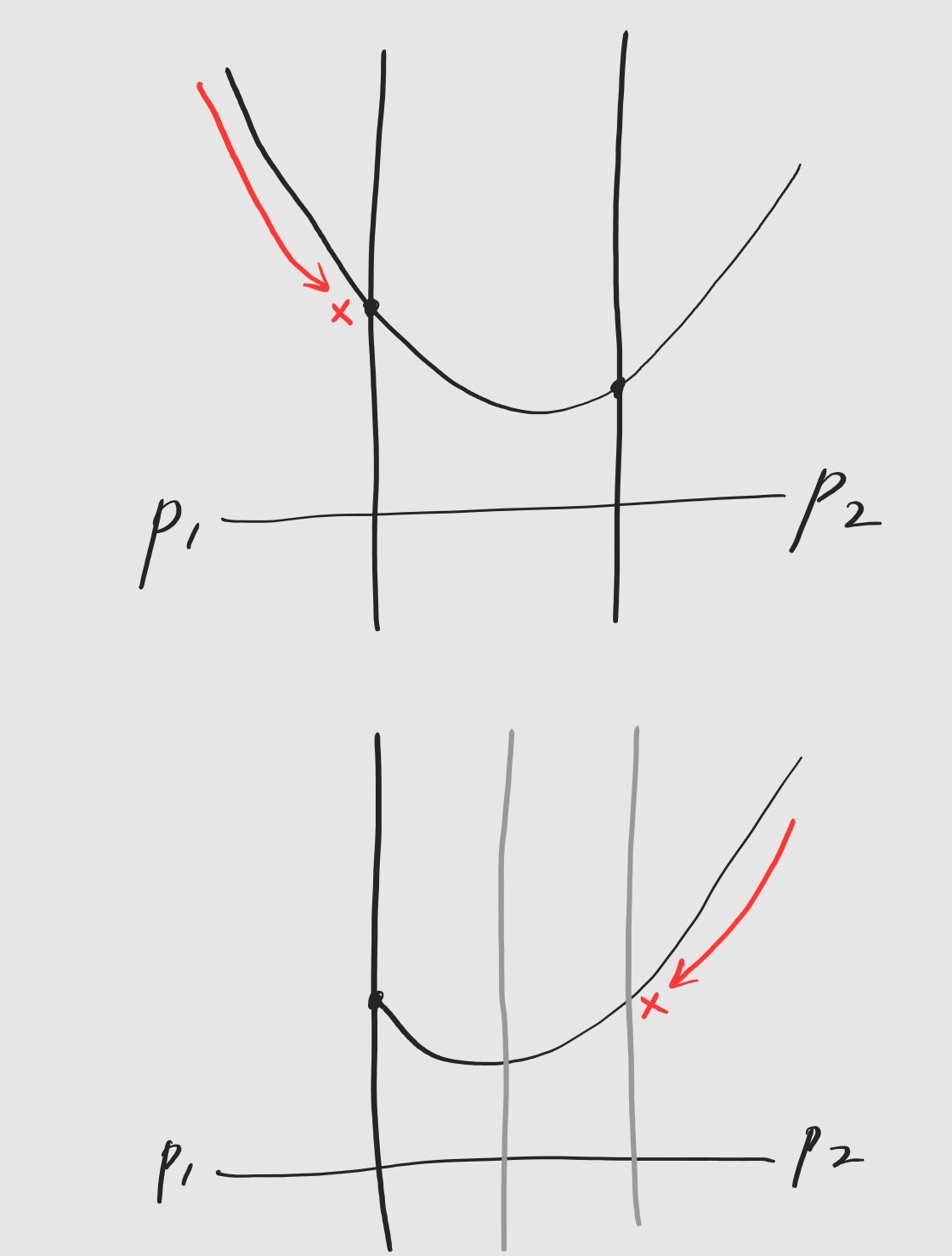
여러 개의 점이 있더라도, 결국 중요한 것은 삼각형과 가장 가까운 점들입니다. 그 뒤에 있는 점은 고려하지 않아도 되죠. 그렇다면 가장 바깥에 있는 점들만 모아서 구간에 대해 조회하면 되지 않을까 싶지만, 단순히 볼록껍질을 만들어서는 답을 찾을 수 없습니다.

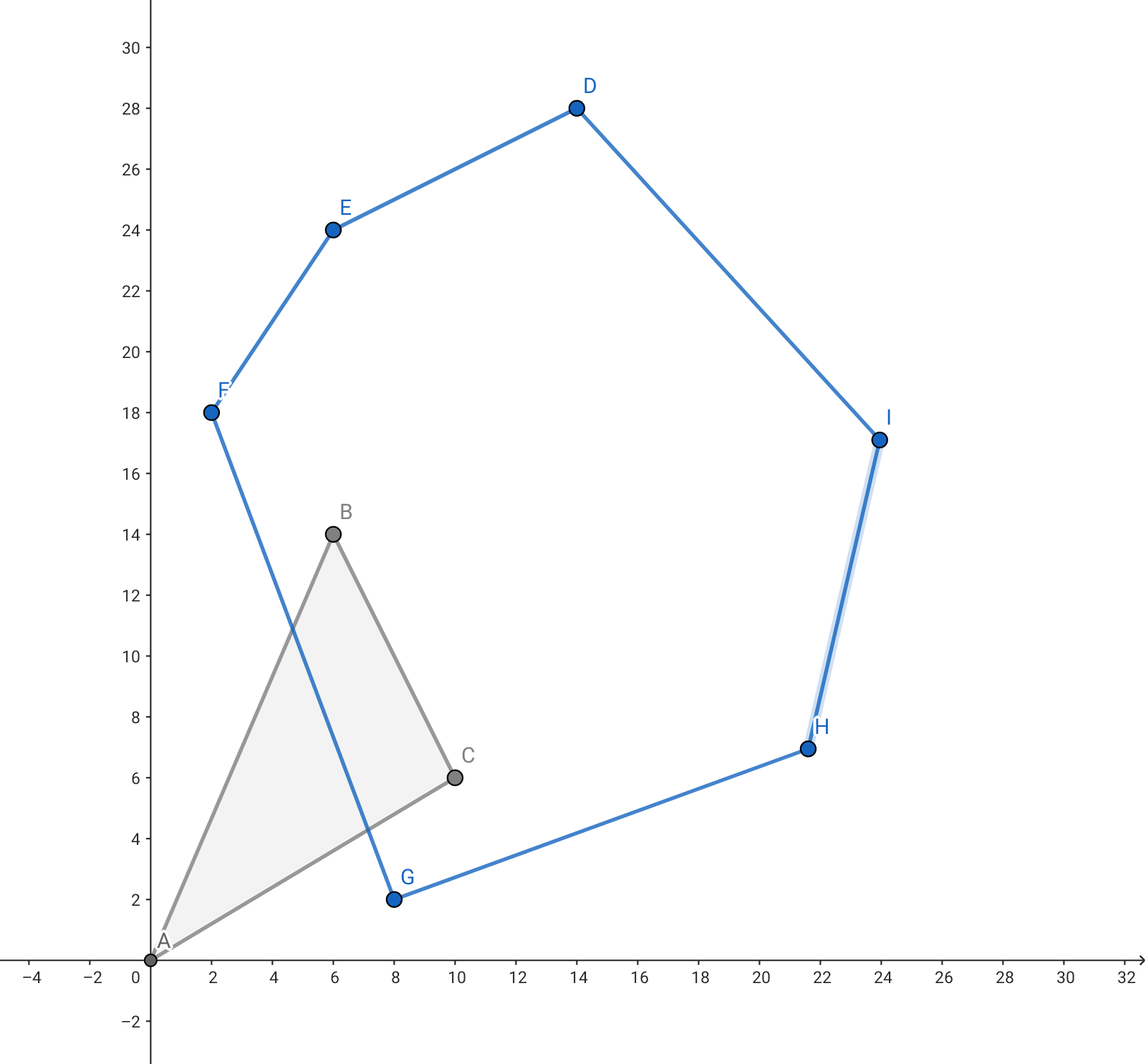
counter

분명 삼각형은 볼록껍질과 교차하지만, 삼각형 안에는 점이 없습니다.

제한된 구간에 대해 유효한 값을 얻기 위해서는, 역시 제한된 구간 내에 존재하는 점들만으로 볼록껍질을 만들어야 합니다. 하지만 이걸 각 쿼리에 대해 수행한다면 시간복잡도는 \(O(QN)\)이 되므로 여지 없이 시간 초과입니다.

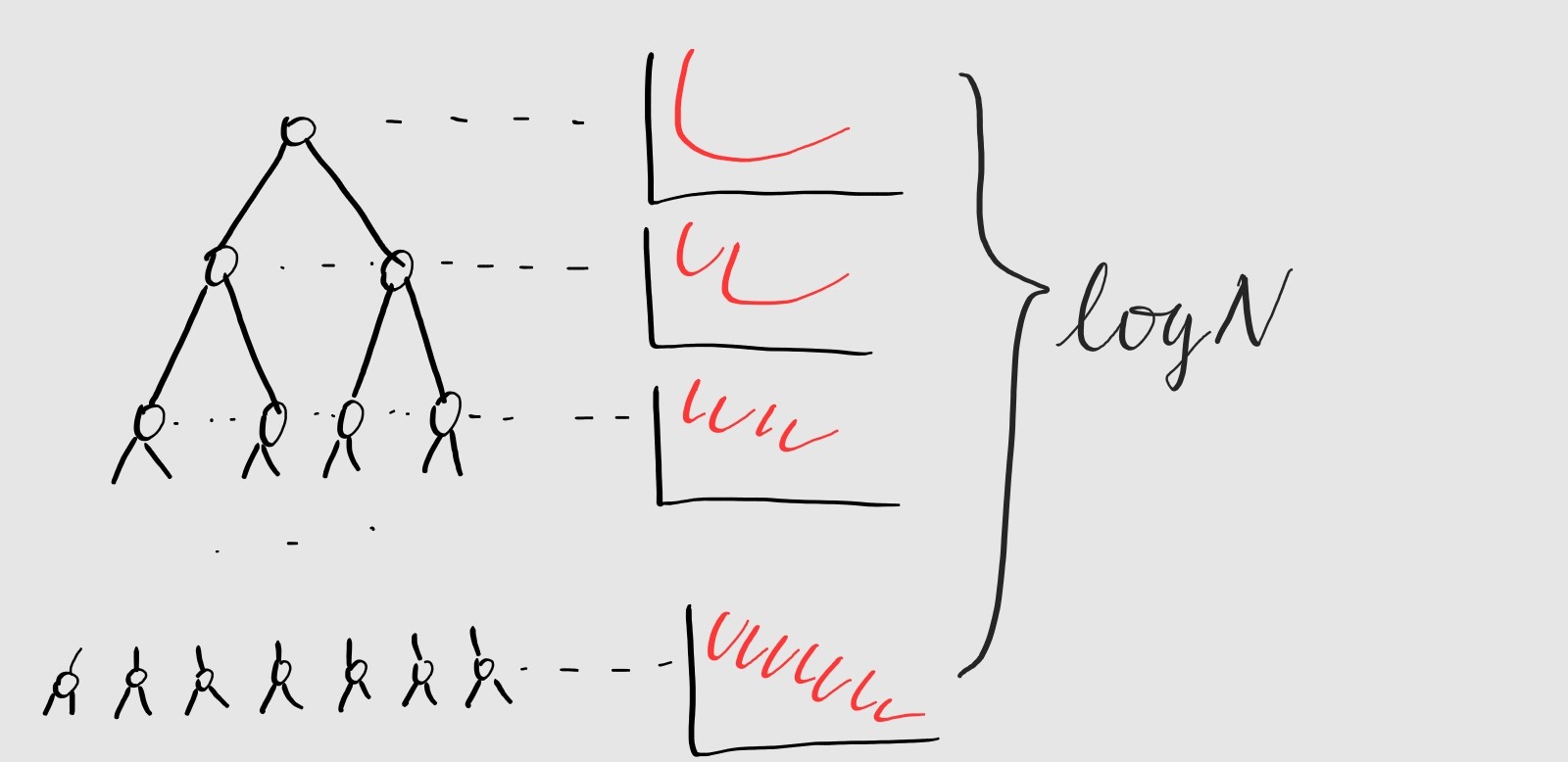
제한된 구간에 대한 쿼리, 이걸 효과적으로 처리하려면 세그먼트 트리를 쓰면 될 것 같은데요. 세그먼트 트리의 각 노드에 볼록껍질을 박아넣는 겁니다. 사실상 그 구조와 메모리의 형태를 보자면 단순한 세그먼트 트리보다는 머지 소트 트리에 가까워지긴 합니다. 어쨌든 구간을 반씩 줄여가면서 beach-line hull을 \(log N\) 개 만들어 두는 것으로 구간 쿼리를 빠르게 처리할 수 있게 됩니다.

beachline-hulls

typedef long long ll;
const int LEN = 100'001;

struct Pos {
	ll x, y;
	bool operator<(const Pos& r) const { return y * r.x > r.y * x; }
	bool operator<=(const Pos& r) const { return  y * r.x >= r.y * x; }
} pos[LEN];

ll cross(const Pos& d1, const Pos& d2, const Pos& d3, const Pos& d4) { return (d2.x - d1.x) * (d4.y - d3.y) - (d2.y - d1.y) * (d4.x - d3.x); }

void monotone_chain(std::vector<Pos>& H, int s, int e) { // 아래 껍질만 따로 구하는 모노톤 체인 컨벡스 헐 알고리즘
	if (e - s <= 1) {
		for (int i = s; i <= e; ++i) H.push_back(pos[i]);
		return;
	}
	for (int i = s; i <= e; ++i) {
		while (H.size() > 1 && cross(H[H.size() - 2], H[H.size() - 1], H[H.size() - 1], pos[i]) <= 0) {
			H.pop_back();
		}
		H.push_back(pos[i]);
	}
}

std::vector<Pos> seg[LEN << 2];

void init(int s, int e, int i = 1) {
	if (s == e) {
		seg[i] = { pos[s] };
		return;
	}
	int m = s + e >> 1;
	init(s, m, i << 1); init(m + 1, e, i << 1 | 1);
	monotone_chain(seg[i], s, e);
}

이제 구간 쿼리 처리하는 방법을 알아봅시다.

제한된 구간에서의 볼록껍질은 구했지만, 아직 껍질 구간 전체에 대한 탐색은 \(O(N)\)이므로 더 줄일 필요가 있습니다. 그래프 개형을 이용하면 삼분탐색을 이용해 이를 빠르게 찾아줄 수 있죠. 다음과 같습니다.

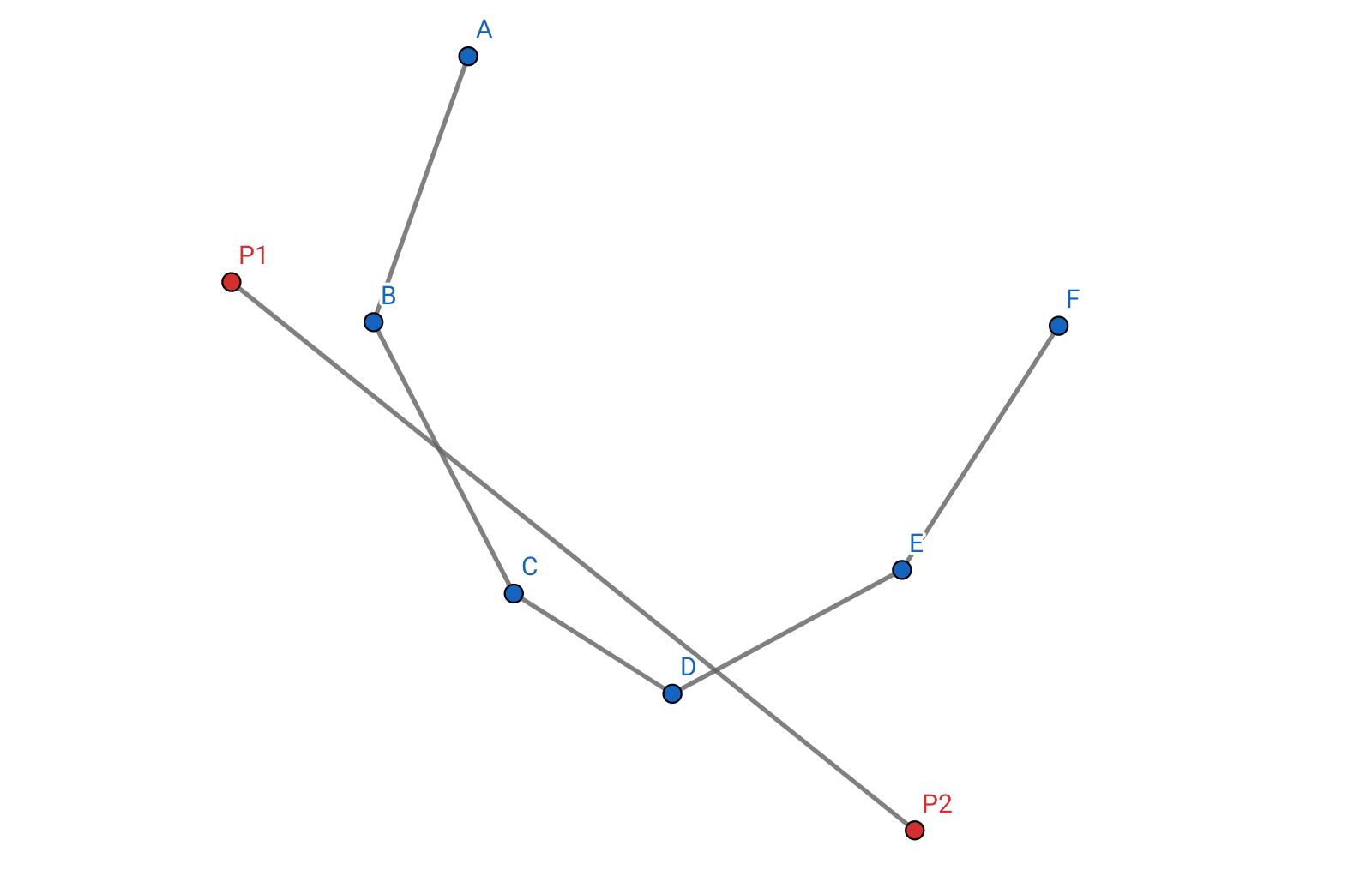
example1

파란 점들로 이루어진 볼록껍질이 있고, 빨간 두 점을 잇는 선분 밑으로 점이 있는지 확인하고 싶습니다. 이를 위해서 외적 값을 계산합니다. \(\overrightarrow{p_1 p_2} \times \overrightarrow{p_2 F}\)를 구하면 다음 평행사변형 넓이를 구하는 것과 같습니다.

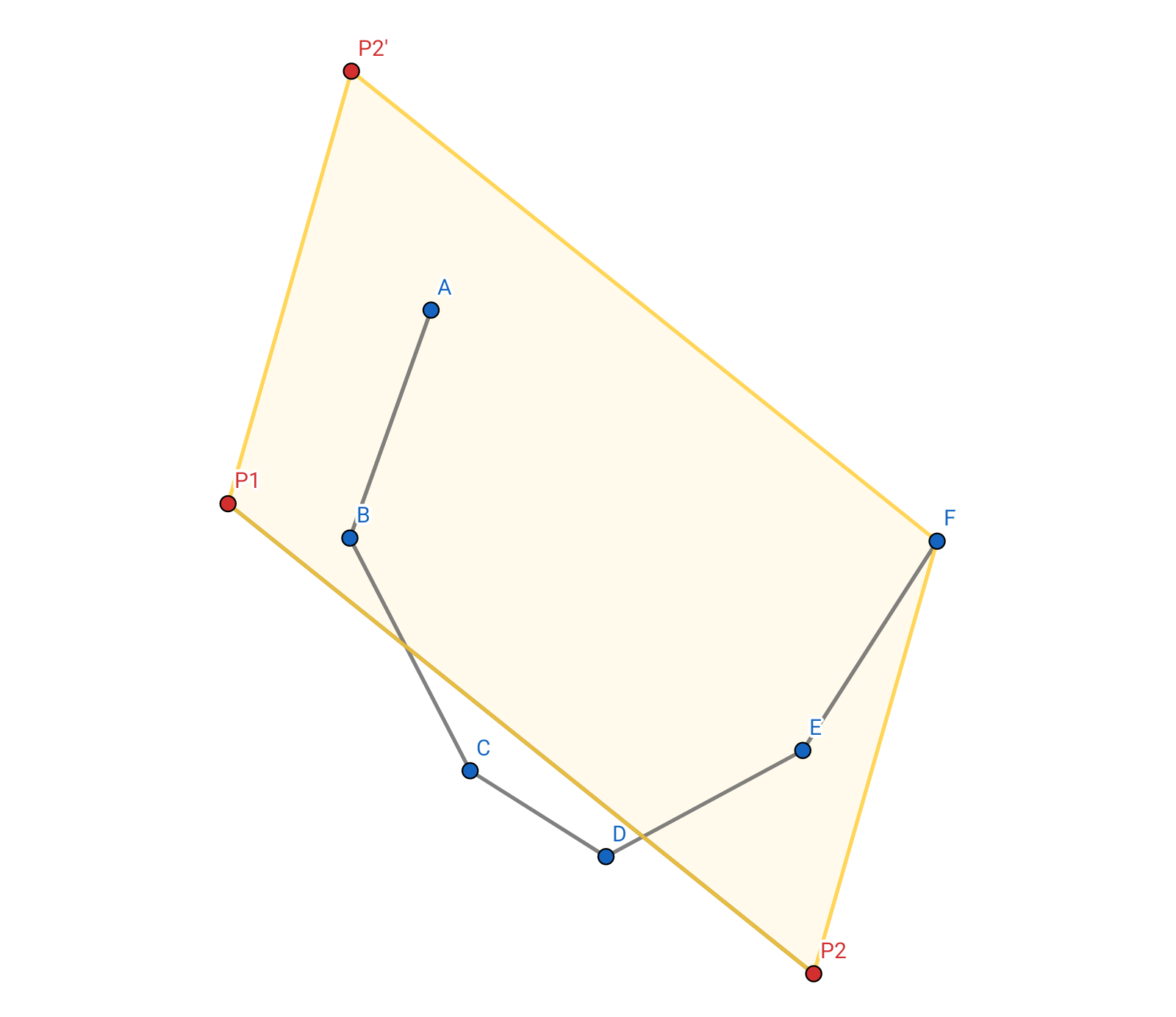
cross_product

이제 껍질의 모든 점들에 대해 외적을 구해줄 건데, 우리는 결국 이 외적 값이 가장 작은 점을 찾는 것이 목표입니다. 위 그림에서 사각형의 넓이는 양수로 계산되고, 점 \(F\)가 선분의 반대쪽에 있다면 넓이는 음수로 계산됩니다. 외적 값이 가장 작을 때의 값이 음수라면, 삼각형 안에 점이 있는 것으로 볼 수 있습니다. 조회하는 점의 개수를 빠르게 줄여나가기 위해 구간을 셋으로 나누고 외적 값이 더 높은 곳을 날려가면서 탐색합니다. (삼분탐색)

ternary

bool ter_search(const Pos& p1, const Pos& p2, const std::vector<Pos>& hull) {
	int s = 0, e = hull.size() - 1, l, r;
	while (e - s >= 3) {
		l = (s * 2 + e) / 3;
		r = (s + e * 2) / 3;
		ll L = cross(p1, p2, p2, hull[l]);
		ll R = cross(p1, p2, p2, hull[r]);
		if (L < R) e = r;
		else s = l;
	}
	for (int i = s; i <= e; ++i) {
		if (cross(p1, p2, p2, hull[i]) <= 0) // 음수라면
			return true; // 삼각형 안에 점이 있습니다.
	}

	return false;
}

그리고 삼각형의 두 점을 이루는 구간은 분할 정복으로 알아서 찾아가게 할 겁니다.

bool search(const Pos& l, const Pos& r, int s, int e, int i = 1) {
	if (r < pos[s] || pos[e] < l) return false;
	if (l <= pos[s] && pos[e] <= r) return ter_search(l, r, seg[i]);
	int m = s + e >> 1;
	return search(l, r, s, m, i << 1) || search(l, r, m + 1, e, i << 1 | 1);
}