백준 1169 - 정사각형 진열
보통 \(O(N^2)\)으로 풀거나 그 이상 걸릴 수 있는 문제를 특정 자료구조를 응용하여 \(O(N)\)등으로 최적화할 수 있는 경우가 있습니다. 정사각형 진열이 그런 문제 중의 하나죠. 한국어로 번역이 되어있긴 한데, 그냥 위에서 보이는 사각형의 수를 찾으면 된다고 하면 될 것을 복잡하게 옮겨놓았네요.
이 문제는 스택으로 \(O(N)\)만에 풀 수 있는 매력적인 문제입니다. 물론 풀이를 잘 찾아야 한다는 게 함정이지만요. 스택에 원소들을 단조적으로 넣는 트릭을 써서 최적화할 수 있습니다. 이 기법을 활용하는 문제를 더 찾아보자면 오큰수나 오아시스 재결합등이 있습니다.
일단 시뮬레이션을 하기 전에 해야 할 작업이 있습니다. 문제에서는 정사각형의 각 변의 길이를 주기 때문에, 실제로는 각 좌표 \(b_i\)는 정수로 표현할 수가 없습니다. 하지만 편의상 사각형들을 \(\sqrt{2}\)배 해줘도 배치되는 형태에는 아무 영향이 없죠. 실수 연산을 배제하는 것은 퍼포먼스 면에서도 정확성 면에서도 하지 않을 이유가 없습니다.
이제 사각형들을 하나씩 차곡차곡 넣어봅시다.
\(i\)번째 정사각형을 넣을 때, 경우는 크게 두 가지로 나뉩니다.
첫 번째 경우는 변의 길이 \(l_i\)가 바로 직전 사각형의 변의 길이 \(l_{i-1}\)보다 짧거나 같을 때입니다. 이 때 \(i\)번째 사각형은 \(i-1\)번째보다 왼쪽에 있는 사각형과는 절대로 접하지 않습니다.
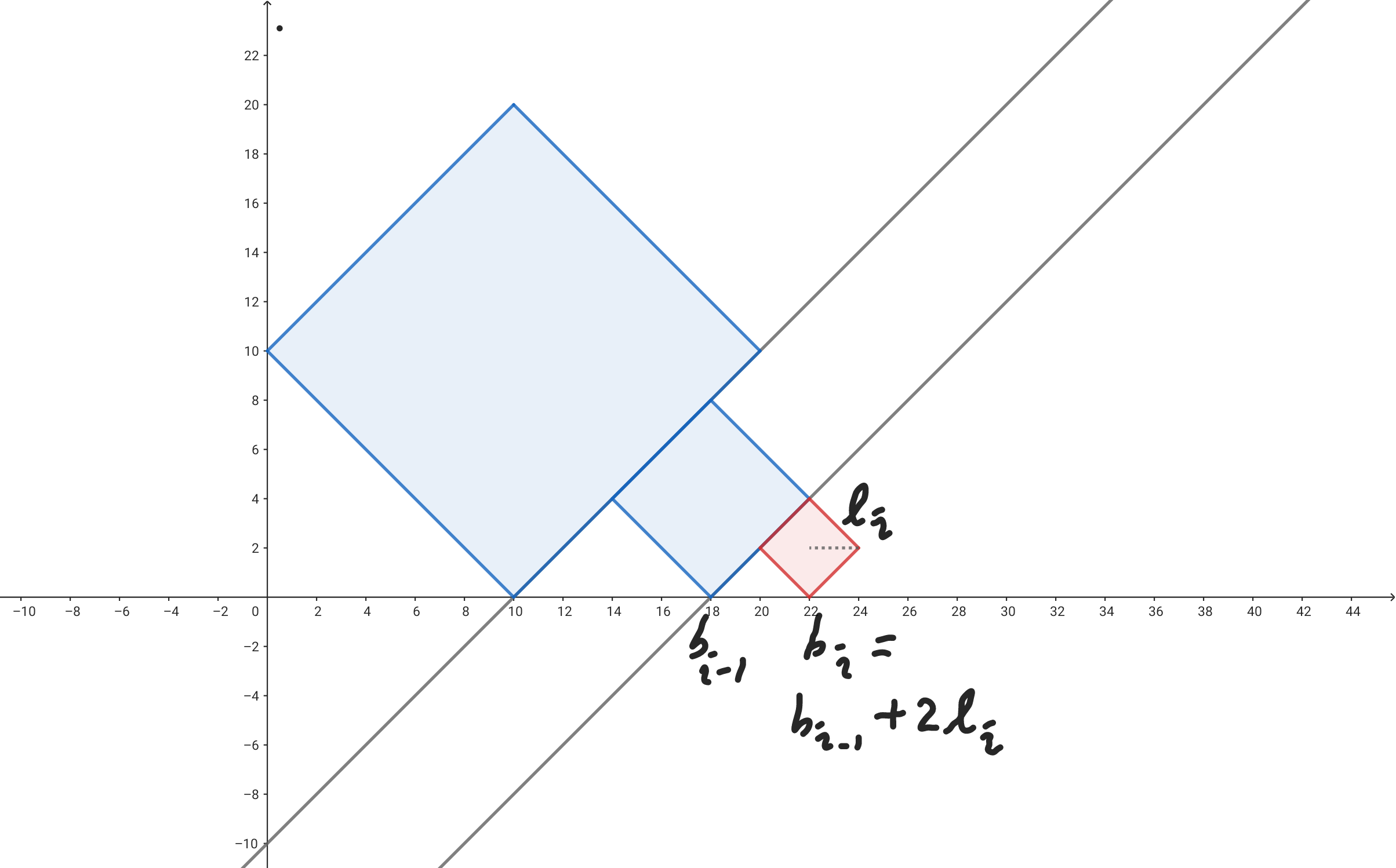
두 번째 경우는 변의 길이 \(l_i\)가 앞의 사각형의 변의 길이보다 길 때입니다. 이 경우는 좀 복잡해집니다. 그 복잡한 과정에서 나타나는 두 가지 특성을 활용하면 스택을 사용하여 빠르게 처리할 수 있게 됩니다.
가장 오른쪽에 있는 사각형과 접할 때까지 밀어본다고 합시다. 이게 가능할 수도 있지만, 그것보다 더 큰 사각형 때문에 실제로는 훨씬 오른쪽에서 멈출 수도 있습니다. 오른쪽에 있는 사각형부터 시작하여 왼쪽에 있는 사각형들과 접하도록 하다보면, 어느 순간엔 더 이상 움직이지 않게 됩니다.
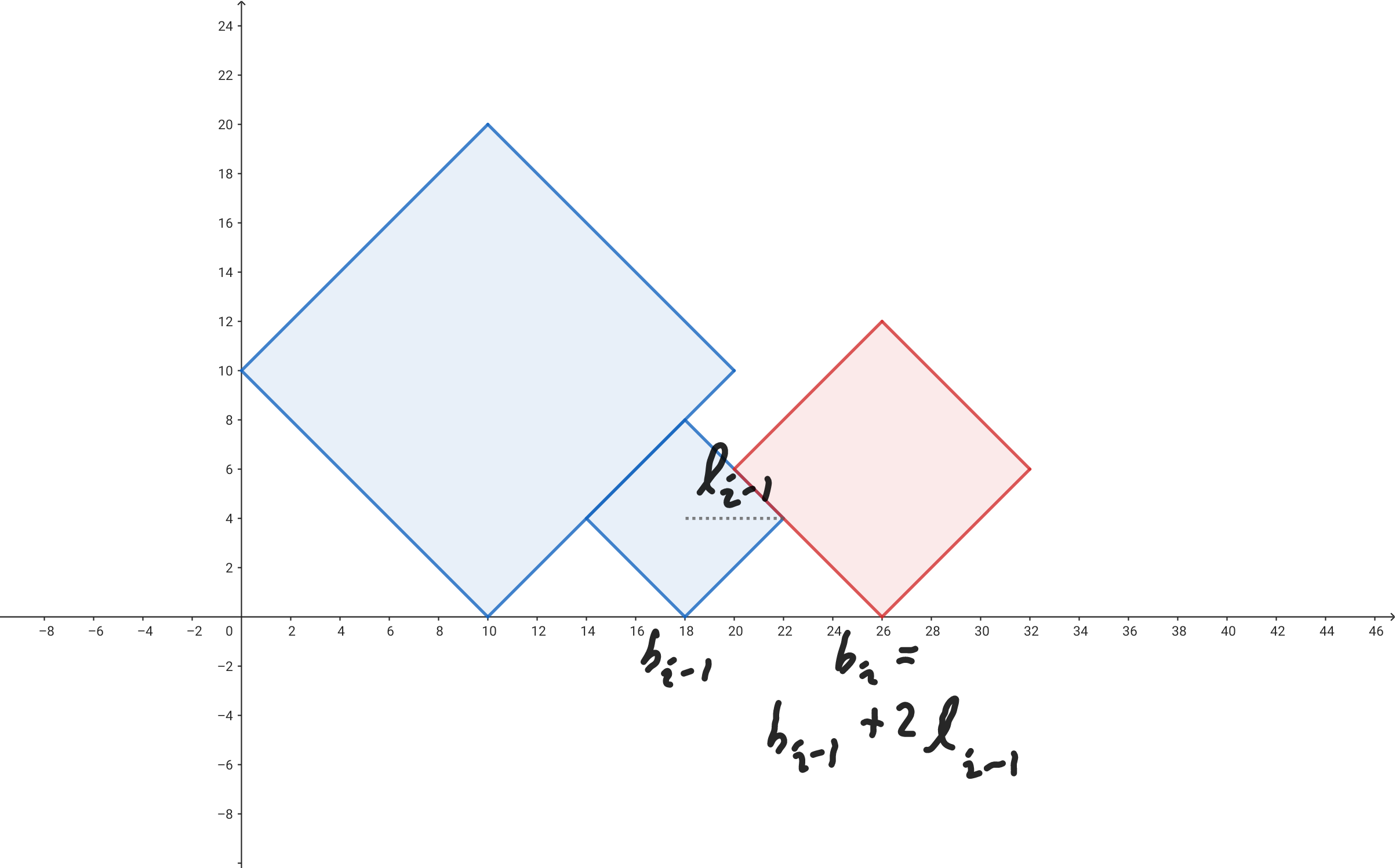
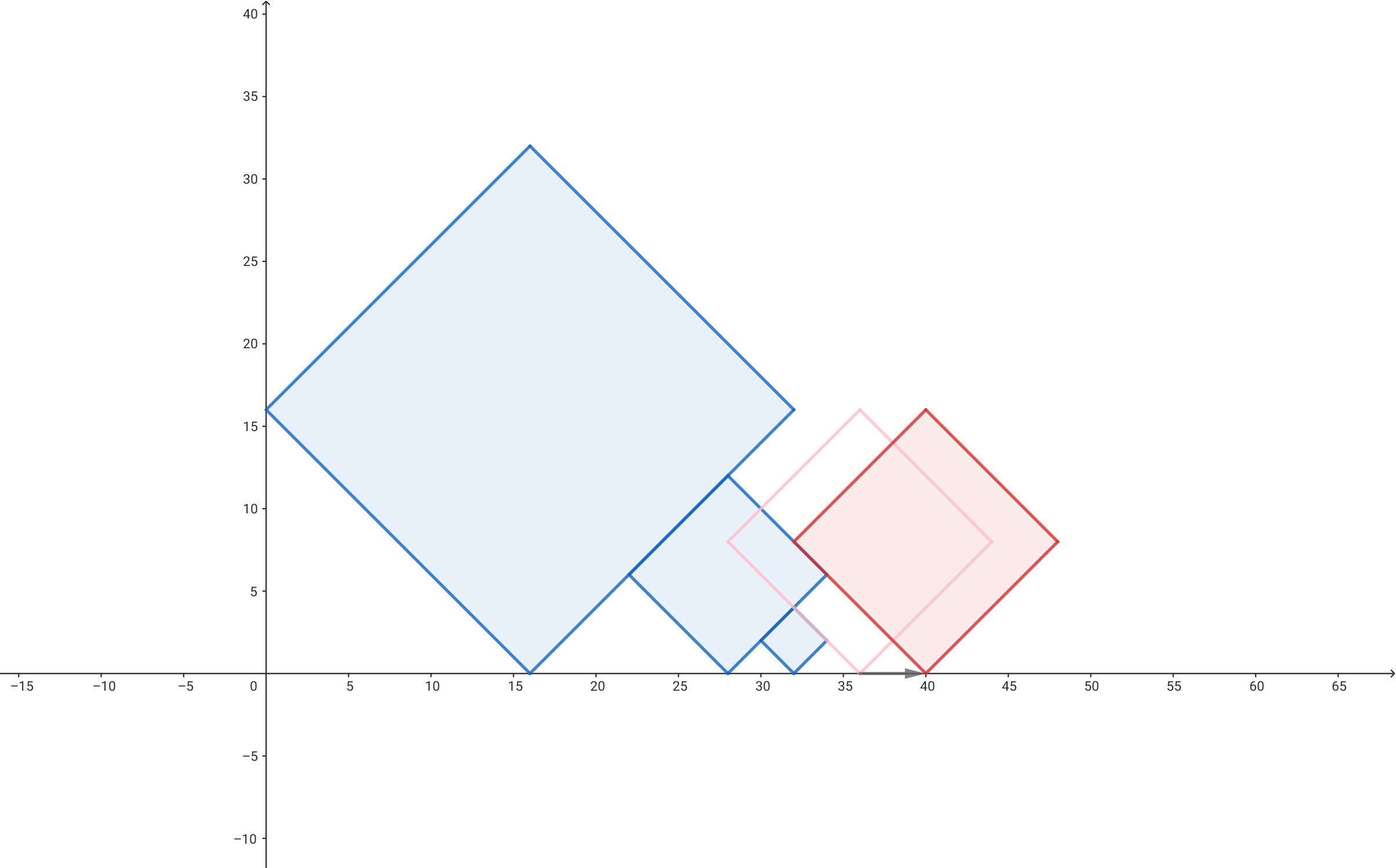
앞의 시뮬레이션에서 꽤나 중요한 것을 관찰할 수 있습니다. 변의 길이가 더 긴 사각형을 오른쪽에 진열했을 때, 왼쪽에 있는 사각형은 덮힌다는 것입니다. 첫 번째 경우에서 변의 길이가 더 짧으면 왼쪽에 있는 사각형과 접하지 않는다고 했는데, 이번엔 반대로 더 오른쪽에 있는 사각형과 접할 일이 없게 됩니다.
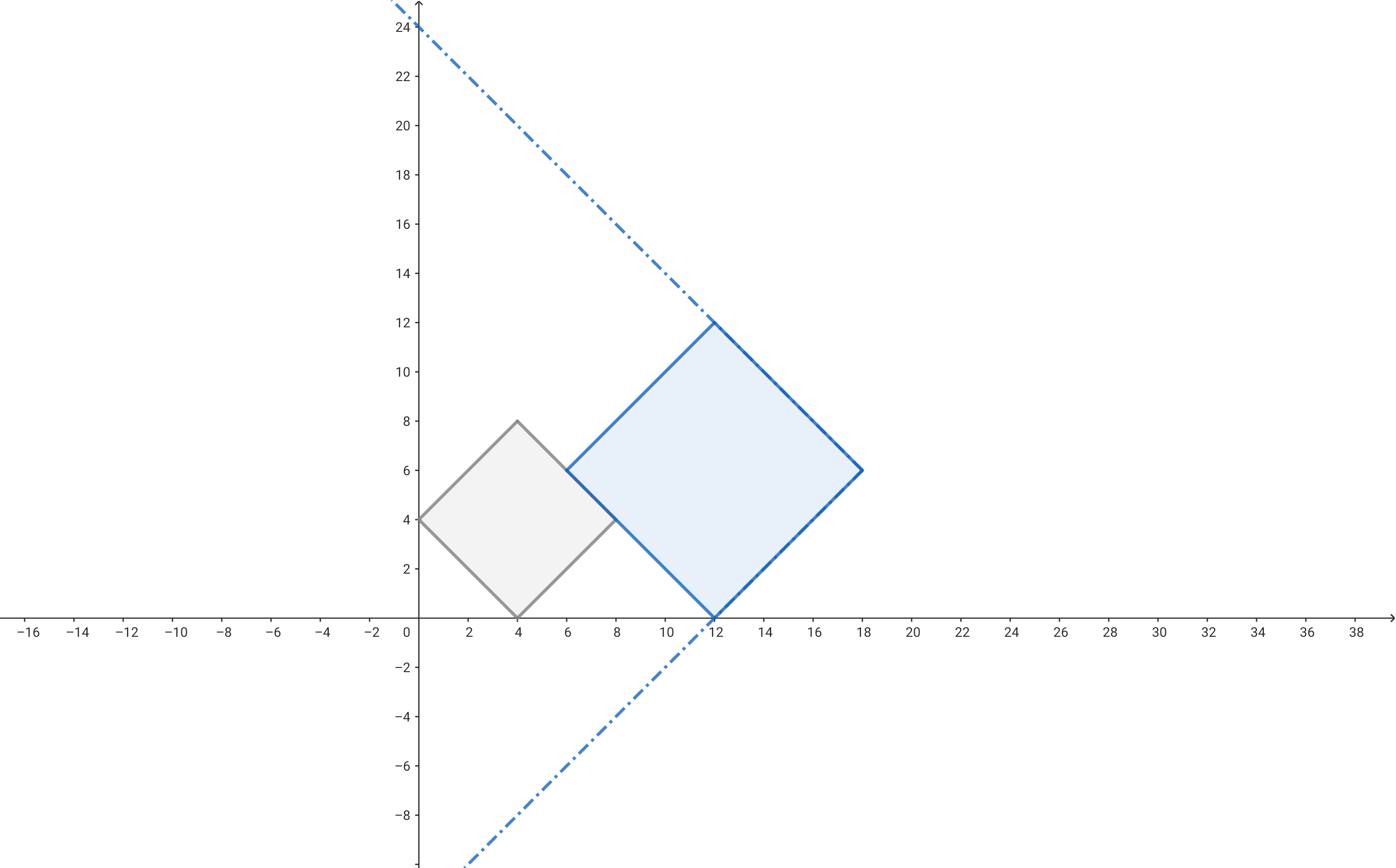
그렇다면 시뮬레이션을 돌리면서 왼쪽에 있는 사각형이 더 작으면 그건 다음 단계에선 더 이상 고려할 필요가 없게 되므로 바로 빼주면 될 것 같습니다. 그렇게 뺄 수 있는만큼 빼주다가 변의 길이가 더 긴 사각형을 만나면 더 왼쪽에 있는 사각형과는 접할 일이 없으므로 멈추는 것이죠. 스택을 쓰면 일련의 과정을 구현할 수 있습니다. 이 과정에서 스택에는 사각형의 크기가 단조적으로 들어갑니다.
const int LEN = 100;
int N, A[LEN], B;
struct Box { int b, l; } stack[LEN];
int sp;
int main() {
std::cin >> N;
for (int i = 0; i < N; ++i) {
std::cin >> A[i];
B = A[i]; // 초기 위치는 A[i]. sqrt(2)를 곱하여 실수 연산을 없애줍니다.
while (sp) {
if (A[i] <= stack[sp - 1].l) { // 변의 길이가 더 짧으면
B = std::max(B, stack[sp - 1].b + 2 * A[i]);
break; // 왼쪽을 더 이상 접하지 않습니다.
}
else { // 변의 길이가 더 길면
B = std::max(B, stack[sp - 1].b + 2 * stack[sp - 1].l);
--sp; // 스택에서 더 작은 사각형을 빼줍니다.
}
}
stack[sp++] = { B, A[i] }; // 스택에 현재 사각형을 넣어줍니다.
}
}
이제 위에서 보이는 사각형들을 찾아봅시다. 스택을 활용하면 이것도 \(O(N)\)으로 시뮬레이션 가능합니다.
이것도 시뮬레이션 전에 문제를 더 단순화해봅시다. 위에서 보이는 사각형을 하나의 선분으로 나타내줄 수 있습니다. 각 선분은 왼쪽 끝 \(l\)과 오른쪽 끝 \(r\), 그리고 높이 \(h\) 값을 가집니다.
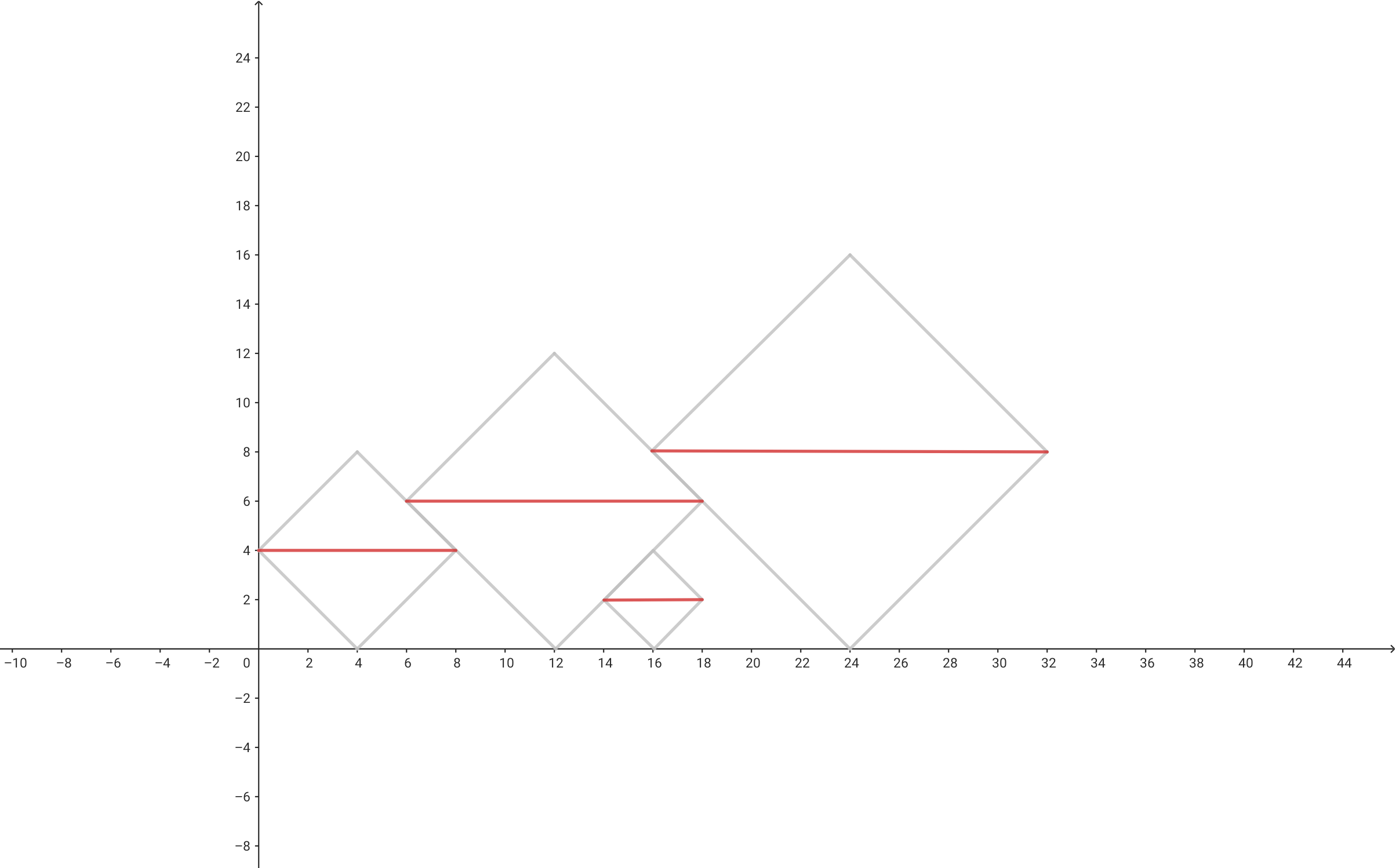
선분들은 정사각형 진열 시뮬레이션 과정에서 \(b_i\) 값이 확정될 때 찾아주도록 합시다.
...
struct Segment { int l, r, h; } seg[LEN];
int main() {
std::cin >> N;
for (int i = 0; i < N; ++i) {
...
while (sp) {
...
}
stack[sp++] = { B, A[i] };
seg[i] = { B - A[i], B + A[i], A[i] };
}
}
두 번째 시뮬레이션 또한 왼쪽에서부터 직선들을 스위핑 하듯 훑으면서 진행합니다. 선분들이 합쳐지는 것은 아니고, 왼쪽으로 좌표가 이동할 수도 있으므로 엄밀하게 스위핑이라 하기는 힘들지만 말이죠. 위에서 선분을 얻는 과정의 특성 상 모든 선분들은 정렬된 상태입니다. 이제 왼쪽 직선부터 차례대로 스택에 넣어줄 겁니다. \(i\)번째 선분을 \(i-1\)번째 선분과 비교할 때도 전과 마찬가지로 크게 두 가지 경우가 생깁니다.
첫 번째로 \(i\)번째 선분이 \(i-1\)번째 선분보다 아래에 있는 경우입니다. 이 때는 완전히 가려 보이지 않게 되거나, 일부가 가리더라도 아직은 보일 수 있습니다. 완전히 가릴 때는 스택에 넣지 않고 넘어갑니다. 일부가 가릴 경우엔 선분의 \(l_i\) 값을 \(r_{i-1}\)만큼 오른쪽으로 밀고 스택에 넣습니다.
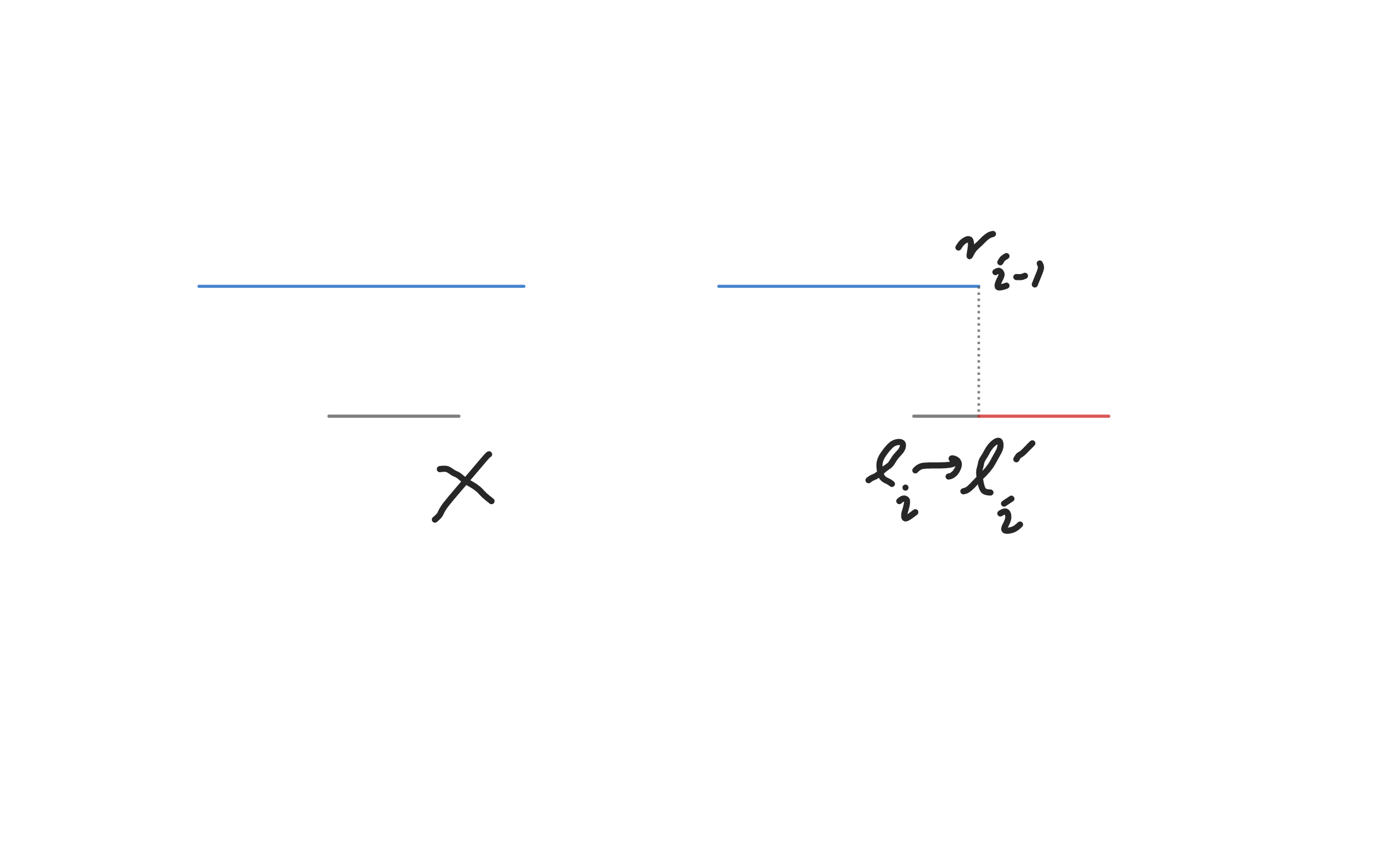
두 번째는 \(i\)번째 선분이 위에 있을 때입니다. 이 때는 현재 선분이 왼쪽에 있는 다른 선분들을 완전히 가리는 경우가 생길 수 있습니다. 완전히 가린다면, 그것들을 스택에서 빼주도록 합니다.
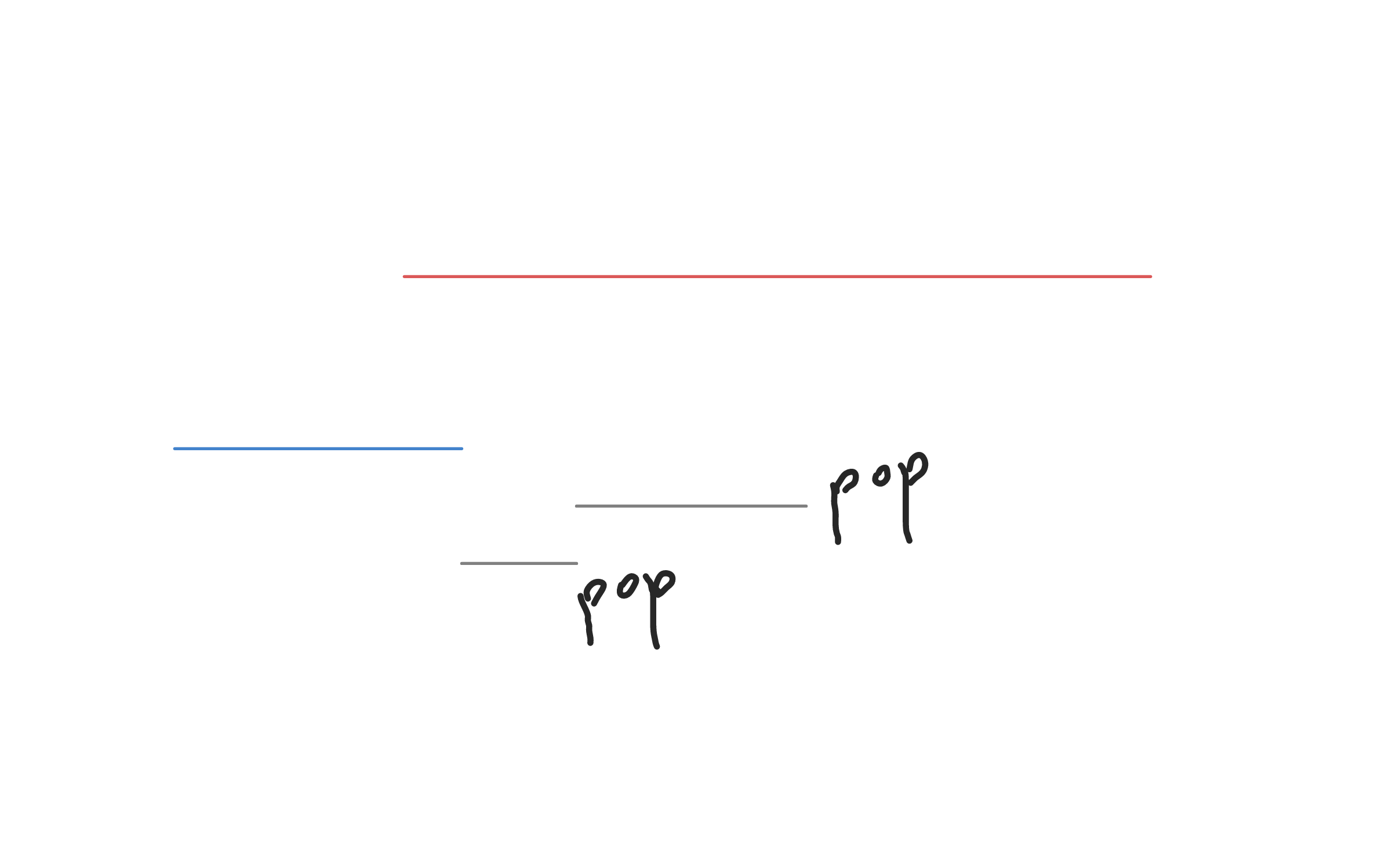
이제 구현을 해봅시다.
struct Segment { int l, r, h; } seg[LEN];
int sp2, stack2[LEN];
int main() {
std::cin >> N;
for (int i = 0; i < N; ++i) {
...
seg[i] = { B - A[i], B + A[i], A[i] };
}
for (int i = 0, j, f; i < N; ++i) {
f = 1;
while (sp2) {
j = stack2[sp2 - 1];
if (seg[i].h <= seg[j].h) { // i번째 선분이 밑에 있다면
if (seg[i].r <= seg[j].r) { f = 0; break; } // 완전히 가리면 스택에 넣지 않습니다.
seg[i].l = seg[j].r; // l 값을 가려지는만큼 이동시킵니다.
break;
}
else { // i번째 선분이 위에 있다면
if (seg[i].l > seg[j].l) break; // 왼쪽 선분이 완전히 가려지지 않으면 그대로 둡니다.
--sp2; // 완전히 가려진다면 스택에서 뺍니다.
}
}
if (f) stack2[sp2++] = i;
}
for (int i = 0; i < sp2; ++i) std::cout << stack2[i] + 1 << ' ';
}