백준 9382 - Solar Eclipse
이번에 풀어본 문제는 상당히 오랜 기간 풀리지 않고 있던 Solar Eclipse입니다. 사실 스스로 느끼기에 최적화를 위한 알고리즘이나 자료구조는 꽤 많이 공부를 한 것 같으면서도 기하학과는 유독 담을 쌓고 살았다는 생각이 들던 차에 약점을 보완하고자 풀어봤습니다.
최근 각국의 과학자들은 화성에서의 일식을 관측하기 위해 앞다퉈 화성으로 향하고 있다. 당신은 일식을 관측하기에 가장 좋은 자리를 찾아야 한다. 화성에서 일식을 관측할 수 있는 태양을 접하고 있는 면을 2차원 평면으로 보고, 일식을 관측하기에 최적인 명당은 편의상 \((0,0)\)이라 하자. 명당에 착륙을 하면 좋겠지만 안타깝게도 다른 발 빠른 과학자들이 이미 명당 근처에 자리를 잡은 탓에, 당신은 다른 우주선들과는 충돌하지 않으면서 명당에 가장 가까운 자리를 찾아 우주선을 착륙시켜야 한다.
당신이 탄 것을 포함해 모든 우주선은 위에서 보았을 때 같은 크기의 원으로 나타낼 수 있다. 착륙이 가능하다는 것은 다른 우주선들과 겹치는 면적이 없음을 뜻하며, 접하는 것은 고려하지 않는다. 다른 우주선들은 이 착륙 규칙을 지키지 않아 서로 겹치는 면적이 있을 수 있다.
착륙 가능한 지점 중 원점과 가장 가까운 지점의 거리를 구하여라.
다른 원들과는 겹치지 않으면서 원점과 가장 가까운 점을 찾으면 되는 문제입니다. 사실 언뜻 문제만 읽고서는 도저히 어떻게 풀지 감도 잘 잡히지 않았는데요. 매개변수탐색으로 착륙 가능한 지점의 거리를 좁혀볼까 했지만 그걸 적용할 껀덕지는 없을 것 같고, 어떻게 접근할지를 몰라 몇 달을 북마크만 해두고 묵혀뒀습니다. 그러던 중 동생과 함께 Convex hull for Disk 문제를 같이 풀기도 하는 등 기하학을 좀 공부하고는 감을 잡았습니다.
일단은 순진하게 접근해보려 해도, 착륙 가능한 지점을 어떻게 찾을지부터가 난관입니다.
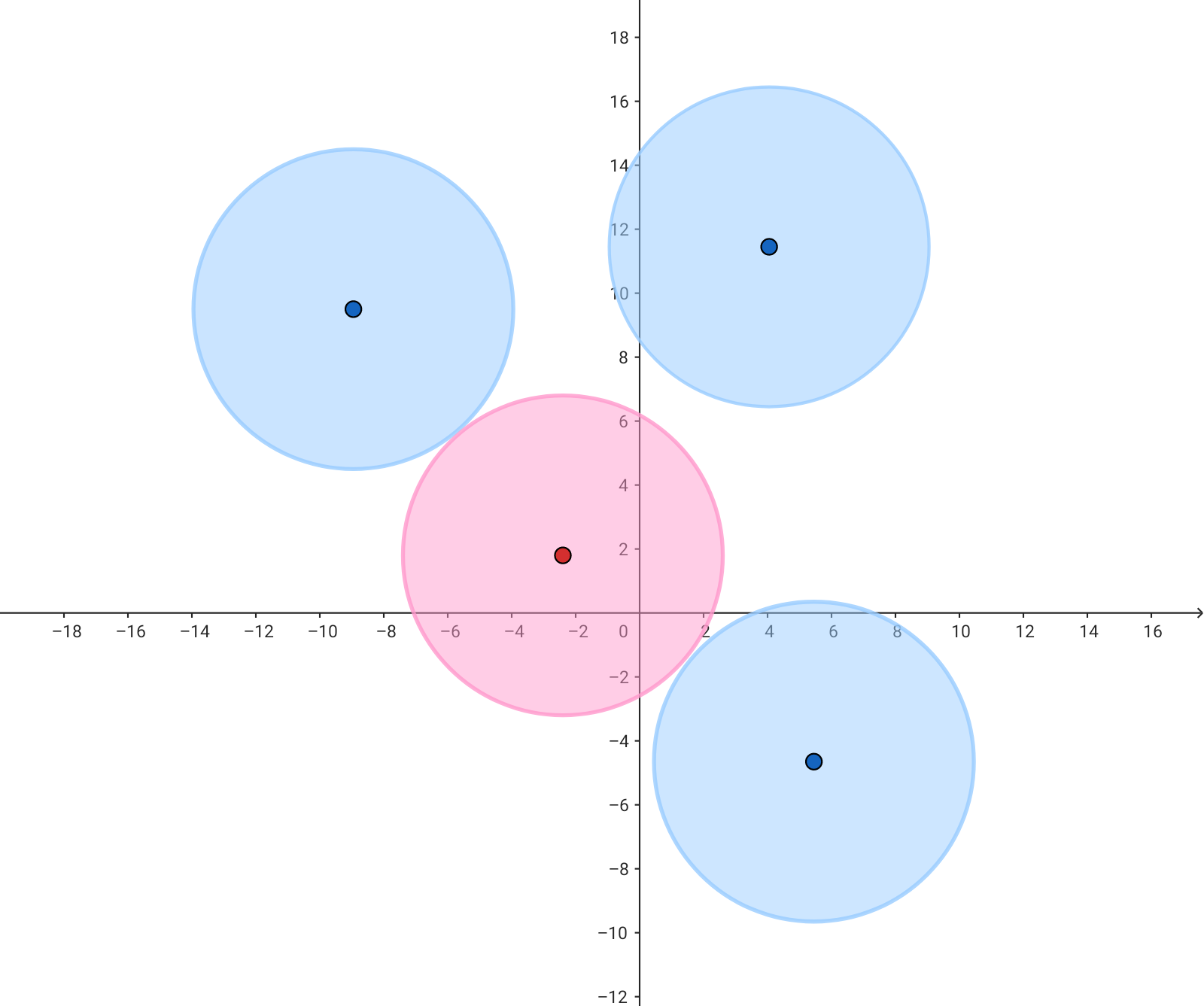
어떤 한 원과는 겹치지 않는 점을 찾았다 해도, 다른 원들과 겹치지 않는지는 다시 검사를 해봐야 합니다. 검사해봐야 하는 점들이 너무 많아지겠는데요. 아무래도 문제를 좀 더 단순하게 만들 방법을 찾아야겠습니다. 애초에 착륙 가능한 지점의 집합을 영역으로 표시할 방법이 있습니다.
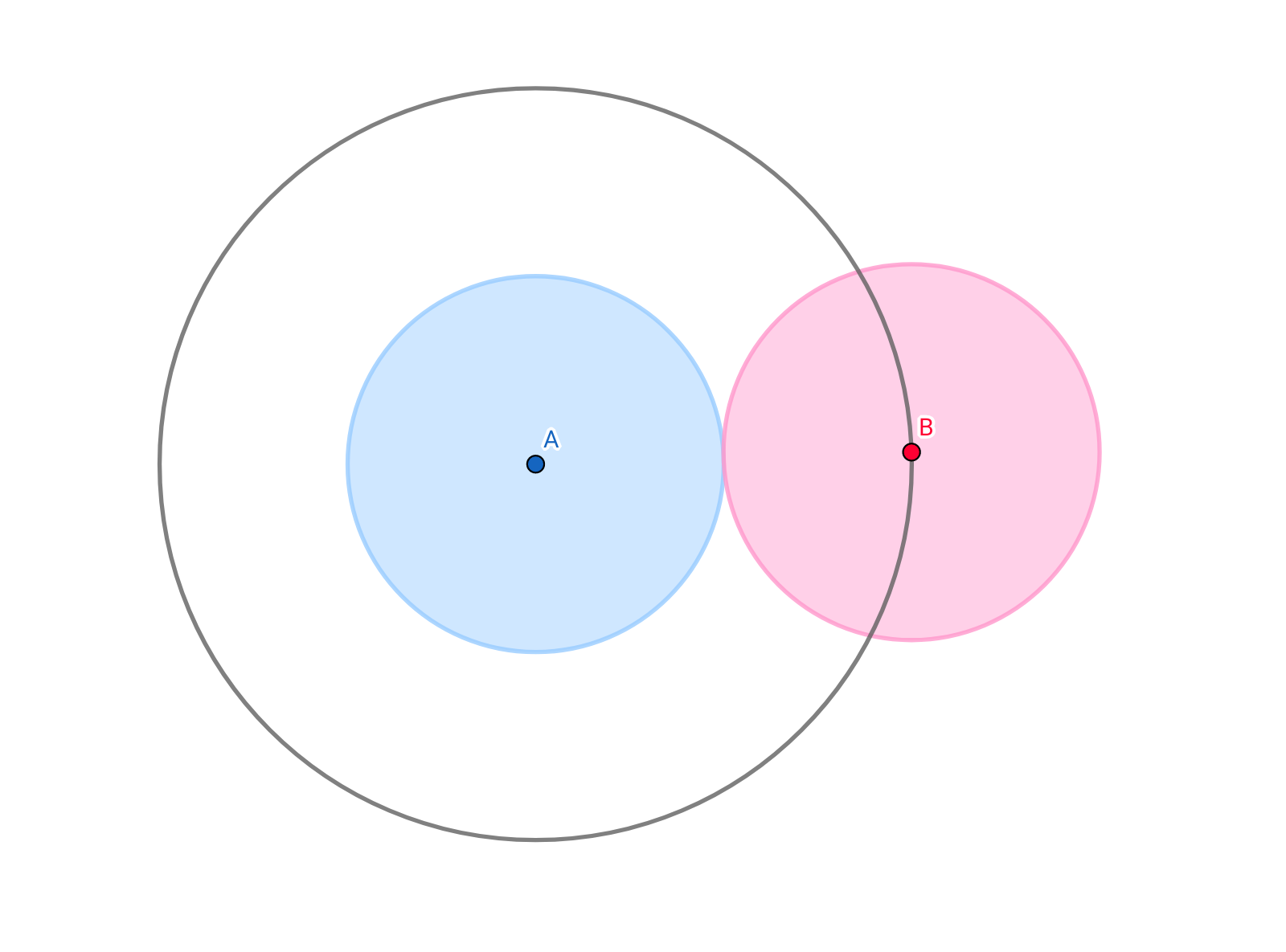
임의의 한 원과 겹치지 않으면서 같은 크기의 원을 그릴 수 있는 영역은 다음과 같이 나타납니다. 반지름이 두 배인 원을 그렸을 때, 그 바깥 영역이 되는 것이죠. 이제 문제에 접근하는 방향을 좁힐 수 있습니다.
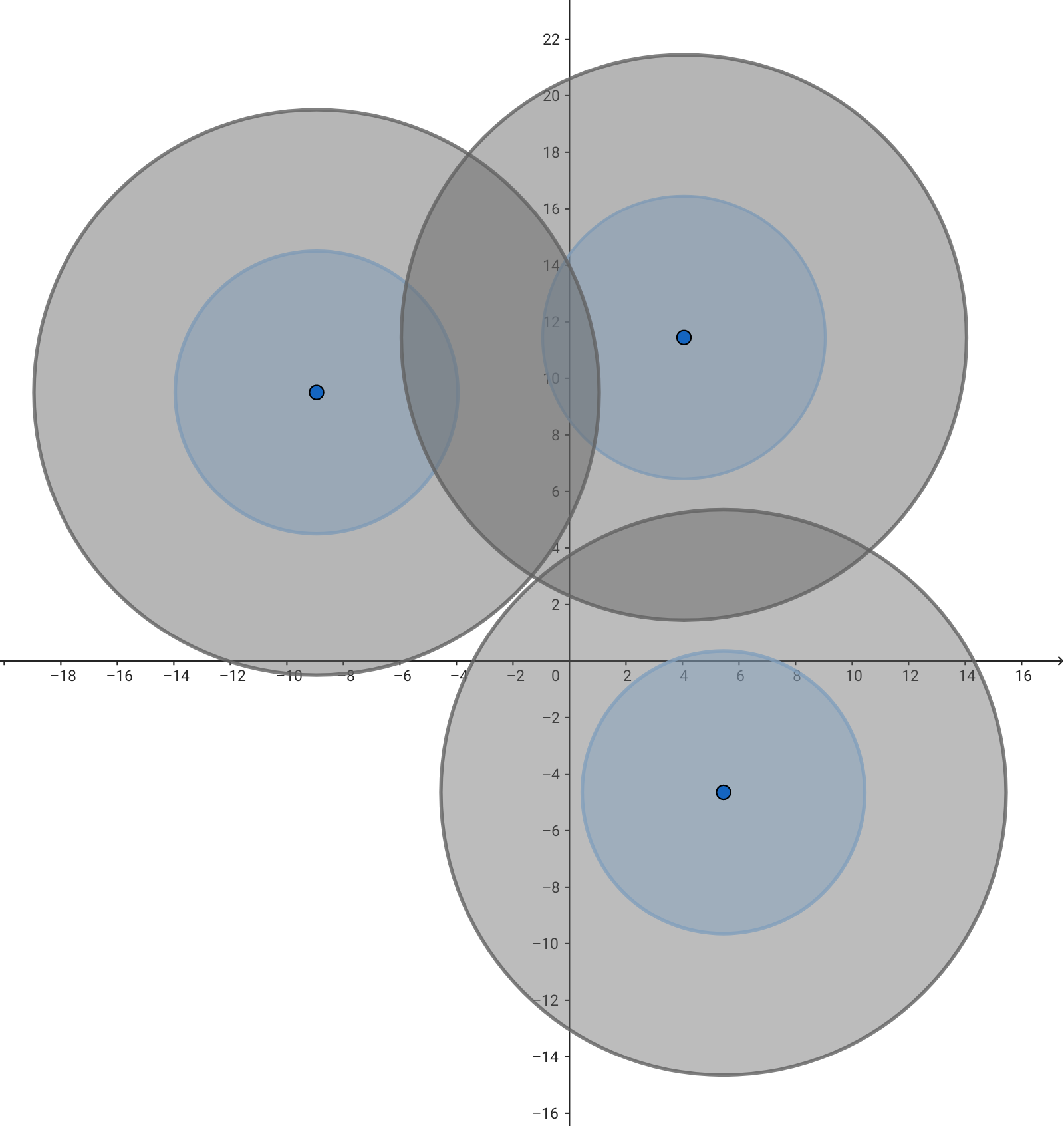
문제에 주어지는 모든 점에 대해, 우주선 반지름의 두 배인 원을 그리고, 그 바깥 영역들의 교집합을 구해줍니다. 그리고 그 영역에서 원점과 가장 가까운 지점을 찾으면 됩니다.
진짜 문제는 여기서부터인데요. 모든 원들이 겹쳐져 만들어지는 호들의 집합을 관리하는 것이 결코 쉬운 일이 아니기 때문입니다. 원이 겹칠 때마다 호를 만들어 넣고, 그 호가 다른 호와 겹치면 그걸 두 개로 갈라 다시 넣고, … 볼록 껍질을 만드는 거라면 자명하게 호의 개수가 \(2N + 1\)개임을 알 수 있기 때문에 괜찮지만, 이건 안쪽까지 모두 고려해줘야 하기 때문에 호의 개수가 몇 개가 될지 알 수도 없는 일입니다. 동생과 꽤 깊은 토론을 해야 했죠.
나: 호가 몇 개나 나올 수 있지? 많아야 \(3N\)개임을 알 수 있을까?
동생: 그렇게 단순하진 않을 것 같은데. 개수도 문제지만 다른 게 더 문제야.
나: 그건 뭔데?
동생: 임의의 호에 대해 원점과 가장 가까운 점을 삼분탐색으로 찾아야 할 것 같다는 거지.
나: 확실히 그래프 개형이 오목하니까 그 점을 찾으면 될 것 같은데… 미적분 같은 걸로 한번에 찾을 수 있지 않나? 애초에 삼분탐색을 해야 하나?
나: ??
동생: ???
임의의 호에 대해, 원점과의 거리를 나타낸 그래프의 개형은 오목하게 또는 볼록하게 나타납니다. 최단 거리가 되는 지점은 하나 존재하는 것이죠. (유일한 반례는 원의 중심이 원점인 경우입니다. 하지만 이 경우엔 모든 정의역에 대해 최단거리이므로 애초에 그래프 개형을 따질 이유가 없습니다) 약간만 생각해보면 최단거리가 되는 지점은 호가 아닌 점으로만 관리해줘도 되고, 단 두 가지 종류의 점들만 찾아주면 된다는 걸 알 수 있습니다.
완전한 원의 경우
일단 호가 완전한 원일 때를 생각해봅시다. 원점이 이 원 안에 있거나 바깥에 있는 경우 두 가지가 있는데, 이 둘 모두에 대해 공통적으로 성립하는 규칙이 있습니다.
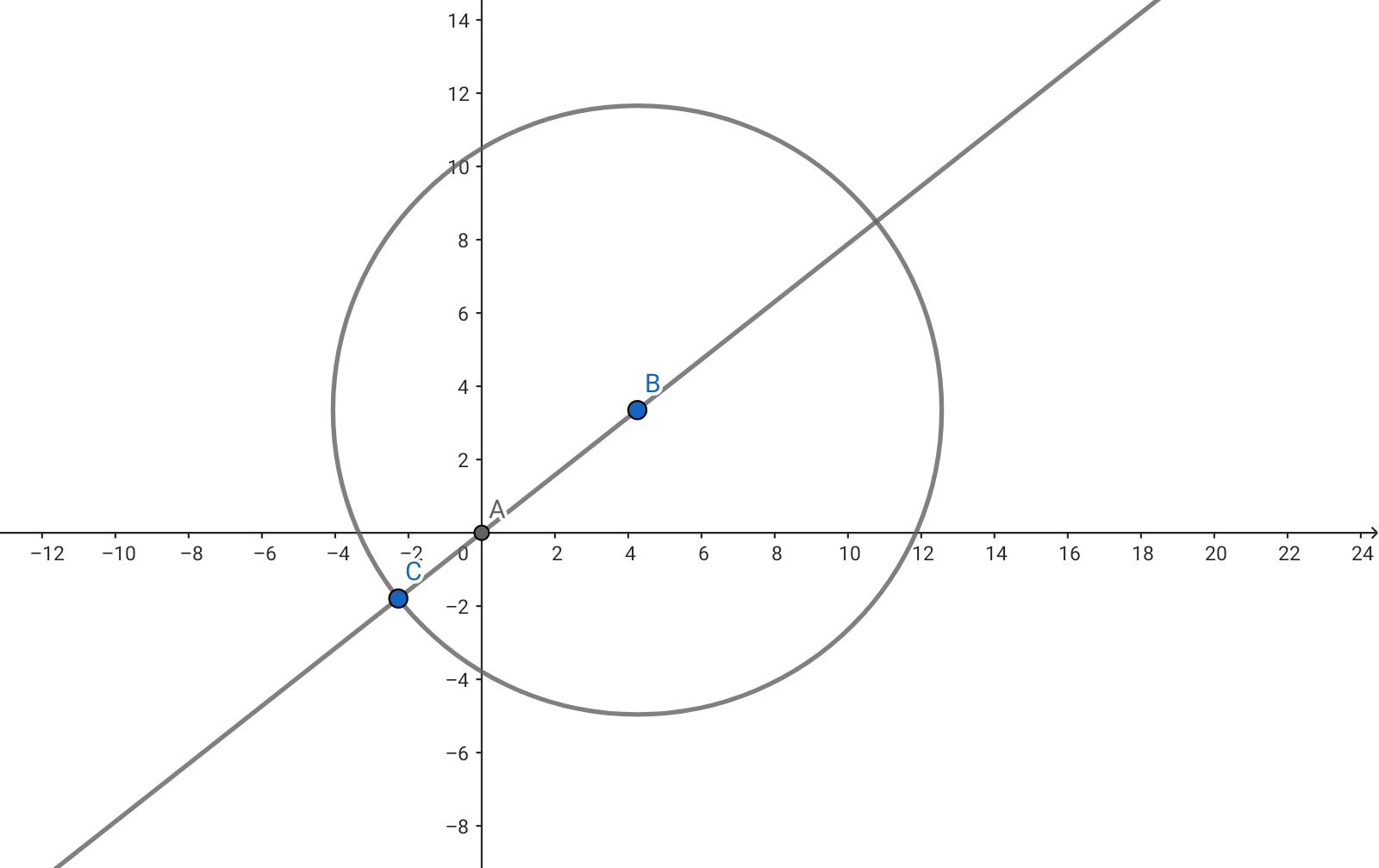
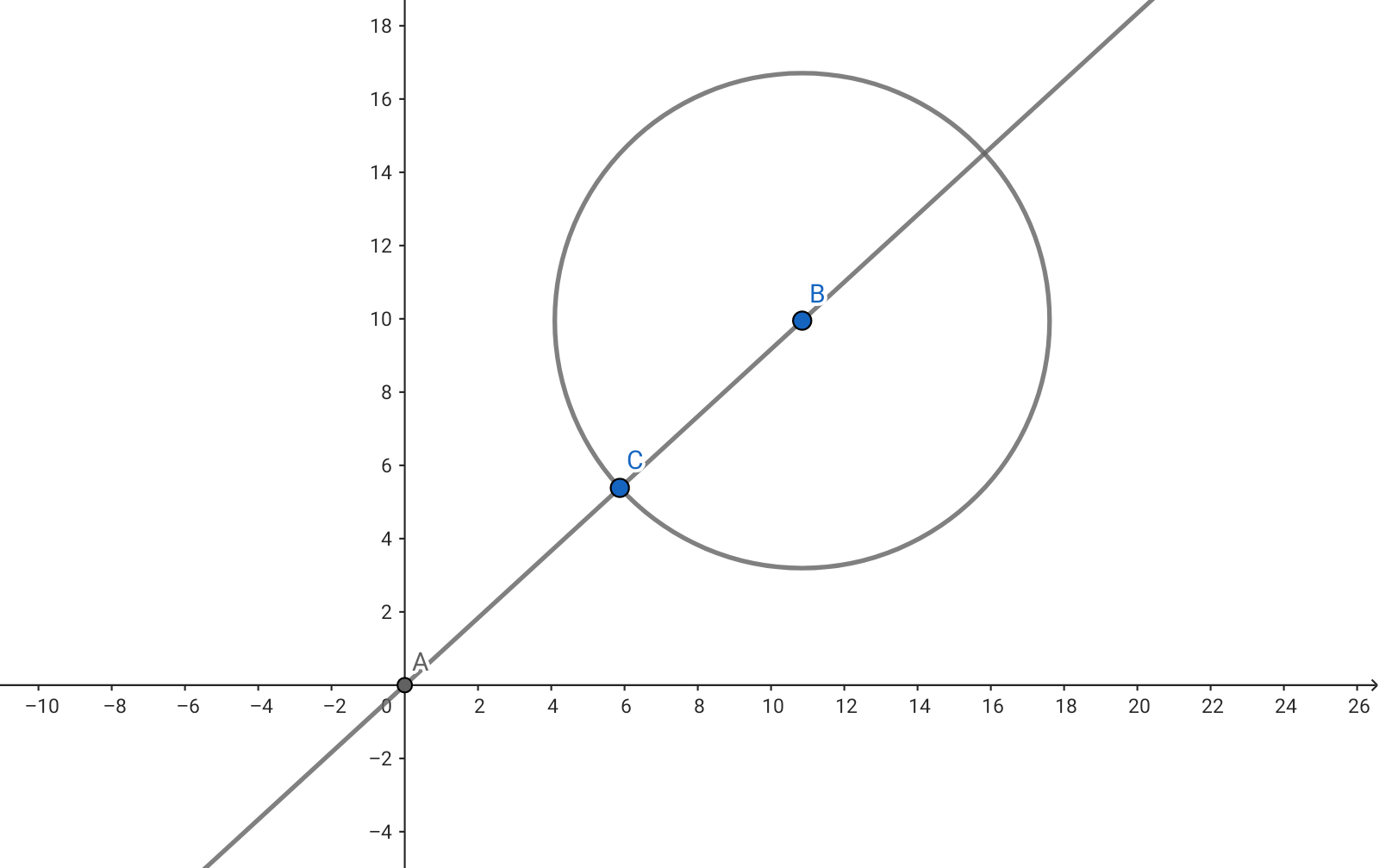
원점과 원의 중심을 지나는 직선을 하나 긋습니다. 그럼 원 둘레와 접하는 점이 둘 생기는데, 둘 중 하나가 항상 원점과 가장 가까운 점이 됩니다. 그리고 그 나머지 한 점이 원점으로부터 가장 먼 점이 됩니다. 이제 소정리 하나를 얻을 수 있습니다.
완전한 원에 대해 원점과 가장 가까운 점은 항상 하나 존재한다.
호가 잘린 구간인 경우
이제 원이 겹쳐서 잘린 경우를 생각해봅시다. 이것도 두 가지 경우를 고려할 수 있습니다.
일단 임의의 구간이 호로 잘리긴 했지만 가장 가까운 지점이 남아있는 경우입니다.
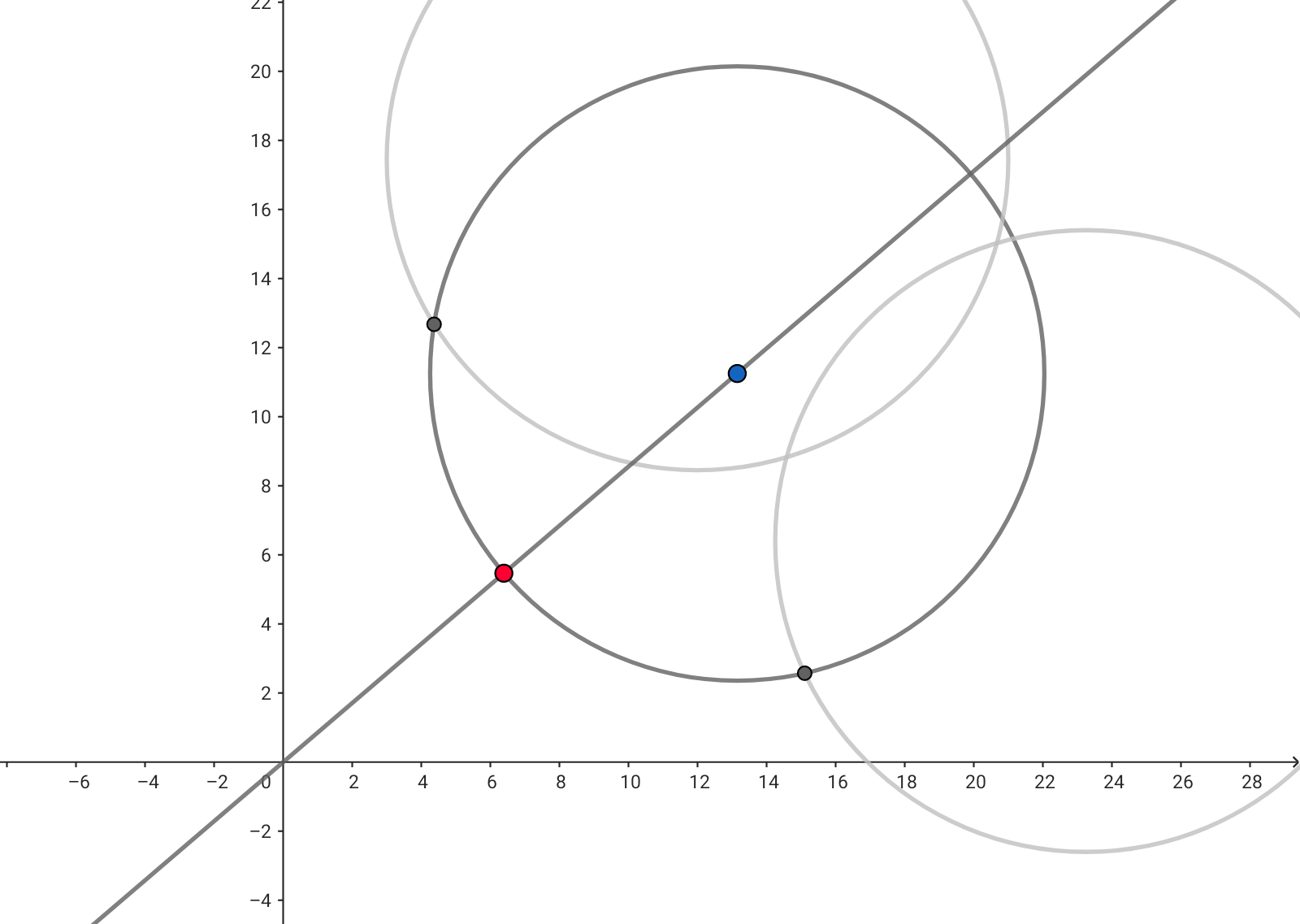
이 때 원점과 가장 가까운 호의 점은 그대로 앞에서 구한 점이 됩니다.
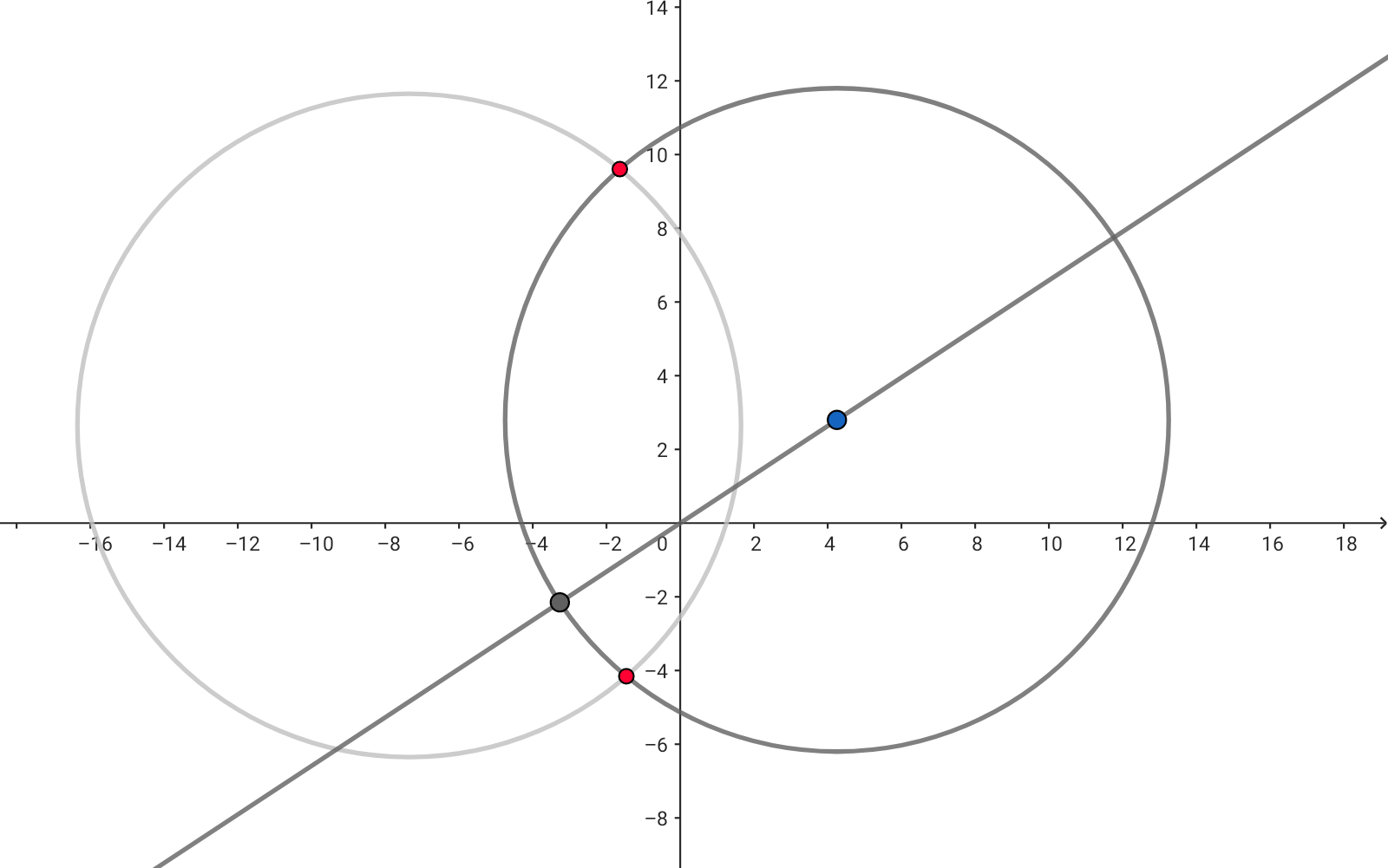
두 번째는 현이 잘리면서 가장 가까운 점이 날아간 경우입니다. 남은 호의 구간에 대해 원점과 가장 가까운 점은 어렵지 않게 찾을 수 있습니다. 가장 가까운 점에서 양 옆으로 움직일수록 원점과의 거리는 항상 멀어지므로, 현의 양 끝 중 하나가 항상 원점과 가장 가까운 점이 됩니다. 이제 정리 하나를 더 얻습니다.
임의의 호에서 원점과 가장 가까운 점은 호의 양 끝 점 중 하나다.
현의 양 끝은 두 원이 겹치면서 생기는 두 교점으로 쉽게 찾을 수 있습니다.
이제 문제는 매우 단순해졌습니다.
- 일단 원점을 찾아줍니다.
- 그리고 모든 원에 대해 일단 원점과 가장 가까운 점을 모두 찾아줍니다.
- 마지막으로 서로 다른 두 원에 대해 겹치는 점들을 모두 찾아줍니다.
- 찾아낸 모든 점들에 대해, 어떤 원 안에도 있지 않으면서 최단 거리인 점을 아무거나 하나 고릅니다.
저는 무식하게 \(O(N^3)\)으로 찾긴 했는데, 더 빠른 방법이 있을 것 같습니다.
#include <iostream>
#include <algorithm>
#include <cmath>
typedef long double ld;
const ld INF = 1e17;
const ld TOL = 1e-7;
const int LEN = 1e6;
int N;
ld R;
struct Pos {
ld x, y;
Pos operator+(const Pos& p) const { return { x + p.x, y + p.y }; }
Pos operator-(const Pos& p) const { return { x - p.x, y - p.y }; }
Pos operator*(ld scalar) const { return { x * scalar, y * scalar }; }
Pos operator/(ld scalar) const { return { x / scalar, y / scalar }; }
} circle[100], candidates[LEN];
const Pos zero = { 0, 0 };
ld distance(const Pos& a, const Pos& b) { return (a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y); }
ld solve(int n, ld r) {
N = 0;
R = r * 2;
candidates[N++] = { 0, 0 };
for (int i = 0; i < n; ++i) {
std::cin >> circle[i].x >> circle[i].y;
ld d = distance(circle[i], zero);
if (distance(circle[i], zero) < TOL) candidates[N++] = { 0, R }; // 유일한 반례인 원의 중심이 원점일 때를 처리
else { // find closest point from circle to zero point
ld ds = sqrtl(d);
Pos v = circle[i] / ds * R;
Pos p1 = circle[i] + v;
Pos p2 = circle[i] - v;
ld d1 = distance(p1, zero), d2 = distance(p2, zero);
if (d1 < d2) candidates[N++] = p1;
else candidates[N++] = p2;
}
}
for (int i = 0; i < n; ++i) {
for (int j = i + 1; j < n; ++j) {
ld d = distance(circle[i], circle[j]);
if (d < TOL || d > R * R * 4) continue; // if two circle are same or too far to intersect, then ignore
Pos mid = (circle[i] + circle[j]) / 2;
Pos w = mid - circle[i];
Pos v = { -w.y, w.x };
ld mw = distance(w, zero);
ld mv = R * R - mw;
v = v / sqrtl(mw) * sqrtl(mv);
Pos p1 = mid + v;
Pos p2 = mid - v;
candidates[N++] = p1;
candidates[N++] = p2;
}
}
ld result = INF;
for (int i = 0; i < N; ++i) {
bool flag = true;
for (int j = 0; j < n; ++j) {
if (distance(candidates[i], circle[j]) < R * R - TOL * 100) {
flag = false;
break;
}
}
if (flag) result = std::min(result, sqrtl(distance(candidates[i], zero)));
}
return result;
}
int main() {
std::cout << std::fixed;
std::cout.precision(6);
int n;
ld r;
while (1) {
std::cin >> n >> r;
if (!n && r < TOL) break;
std::cout << solve(n, r) << '\n';
}
}