백준 30271 - Cleanup | Jay’s blog

이번에 풀어볼 문제는 비교적 최근에 추가된 Cleanup입니다.

큰 태풍이 휩쓸고 간 자리를 청소하는 건 상당한 시간을 필요로 한다. 당신은 이제 곳곳에 널브러진 잔해들을 청소할 계획을 세워야 한다.

쓰레기를 청소하는 것은 크게 두 가지 작업으로 이루어진다.

불도저로 잔해를 밀어 특정 위치에 무더기를 만든다.
잔해 또는 무더기를 트럭에 실어 보낸다.

트럭에 실어 보내는 절차는 무더기의 양과 관계 없이 하나 당 $T$ 시간이 소요된다. 운전기사는 상당한 양의 서류 작업을 마쳐야 하고, 이에 반해 차를 끌고 가서 싣는 것은 무시할 수 있을 정도로 빠르다고 가정한다.

잔해들은 편의상 이차원 직선 상에 널브러져 있다고 하자. 잔해의 양을 $u$, 이동 거리를 $d$라 할 때, 불도저로 잔해를 미는 데는 $ud$ 만큼의 시간이 소요된다.

불도저를 이용해 잔해를 적당히 밀어 몇 개의 무더기를 만들고 불도저의 모든 작업이 끝난 후에는 트럭을 불러 각각의 무더기를 처리장으로 보내려고 한다. 이제 당신은 모든 잔해를 치우는 최소 비용을 구해야 한다. 물론 잔해를 전혀 밀지 않을 수도 있지만, 그건 최적의 해가 아닐 가능성이 높다.

$K$개의 테스트케이스가 주어진다. 각 테스트케이스에 대해 잔해의 수 $n$과 트럭의 비용 $T$가 주어진다. 다음줄에는 $n$개 잔해 $i$에 대해 각각의 위치$l_i$과 크기 $d_i$가 주어진다.

일단 생각해볼 것은 무더기를 만드는 규칙입니다.

불도저를 이용해 민다고 하니, 어떤 점에서 밀기 시작하면 마주치는 모든 잔해를 밀어야 할 것 같지만, 그렇지 않을 수도 있다는 생각이 들긴 합니다. 또한 잔해를 꼭 한꺼번에 다른 곳으로 밀지 않고 일부만 따로 옮길 수도 있지 않을까요. 하지만 둘 다 그럴 필요 없습니다.

일단 잔해의 일부만 따로 옮기는 경우를 생각해봅시다. 잔해를 트럭에 싣고 옮기는 비용은 그 양과 관계 없이 일정하며 제한도 없으므로 양 때문에 나눠 옮기는 일은 없습니다. 일부를 밀고 남은 잔해는 반대로 옮긴다고 해도 그 비용은 전혀 달라지지 않습니다. 따라서 특정 위치의 잔해는 그냥 한꺼번에 밀어도 최적 비용을 구할 수 있습니다.

rule

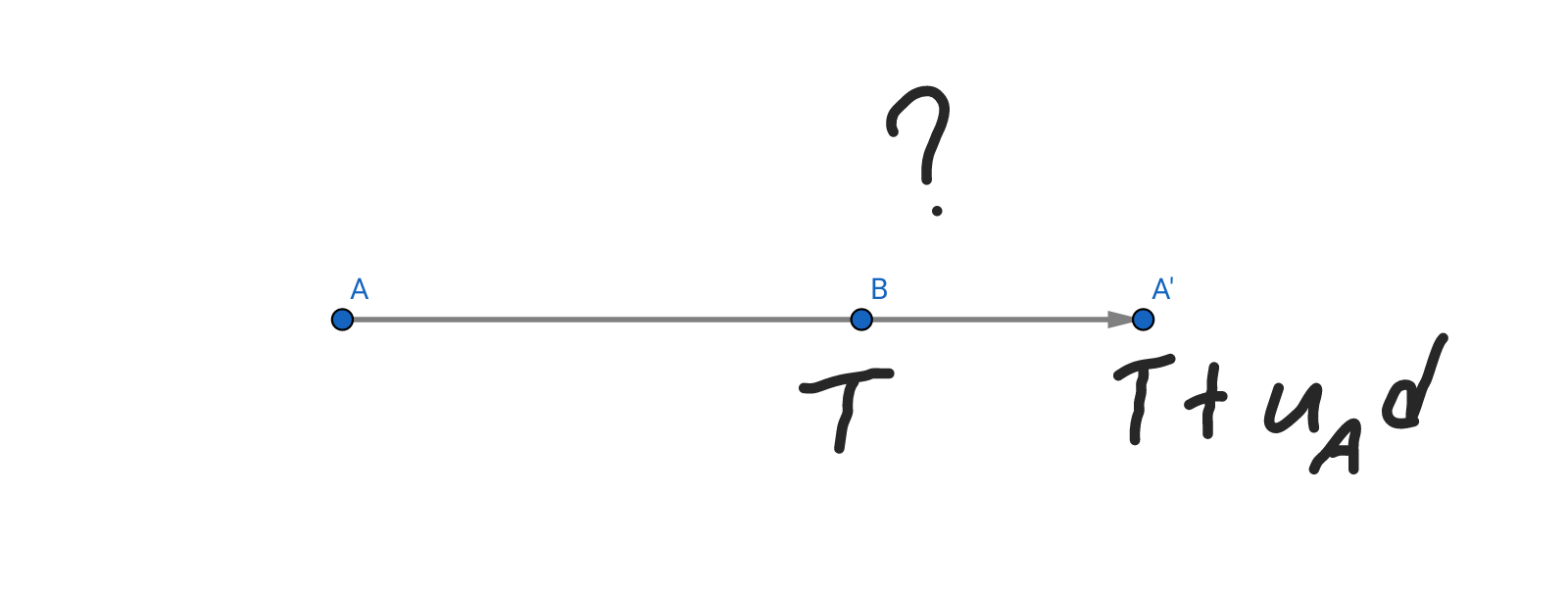
이번엔 어떤 잔해를 무시하고 미는 경우를 따져봅시다. 잔해 A를 밀어 B를 지나친다고 할 때, 이를 처리하는 비용은 잔해 B를 따로 싣는 $T$와 A를 따로 싣는 $T$가 두 번 발생합니다. 만약 B 위치에서 싣는 것이 최적이라면, A를 굳이 더 멀리 옮길 필요가 없습니다. B 위치에서 싣는 것이 최적이 아니라면, B를 굳이 지나칠 필요가 없습니다. 따라서 우리의 불도저는 그냥 우직하게 마주치는 모든 잔해를 밀면서 나아가면 됩니다.

이제 무더기를 만드는 위치를 생각해봅시다. 임의의 위치에 만들 수는 있지만, 최적의 위치는 항상 정해져 있습니다.

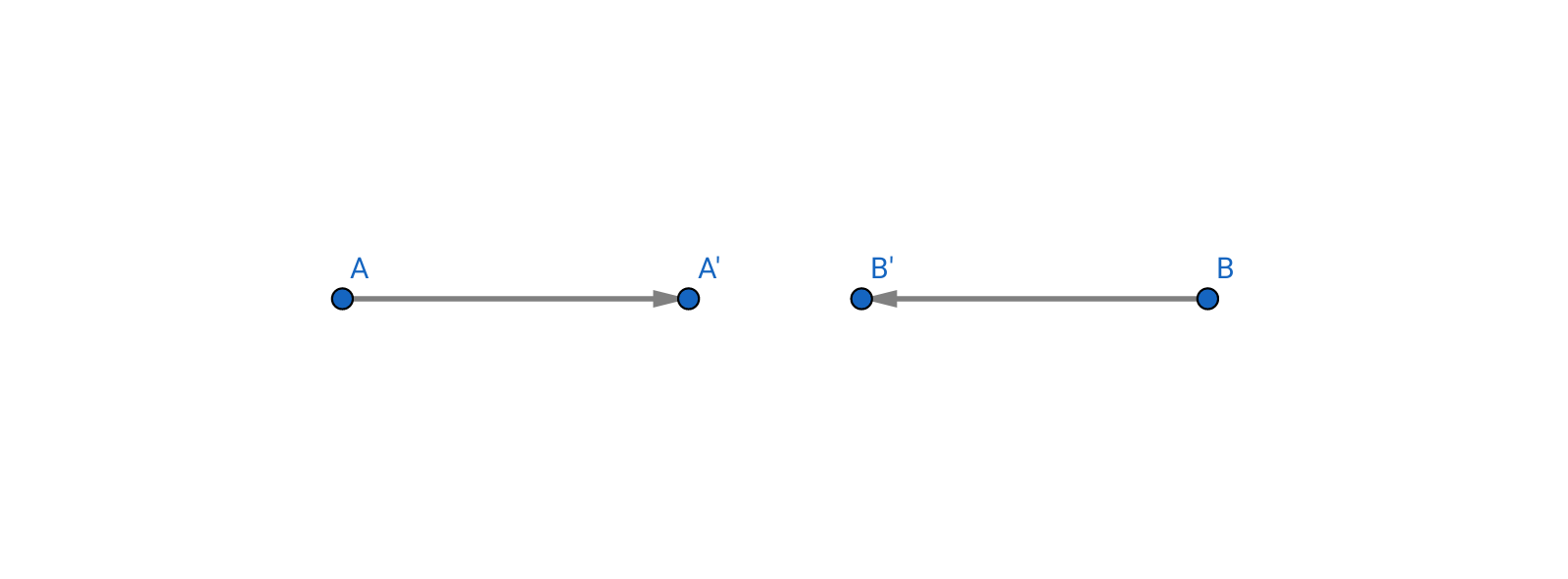
example1

만약 양쪽 잔해 또는 무더기의 양이 같을 때는 양 끝을 벗어나지만 않는다면 어느 곳에 밀어다 놓더라도 그 비용은 일정합니다. 양 잔해가 이동하는 길이의 합이 항상 같으므로 영향이 없습니다. 그렇다면 어느 한 쪽으로 몰아넣어도 그 비용은 최적입니다.

example2

어느 한 쪽 잔해 또는 무더기의 양이 더 많다면 말은 달라집니다. 양이 적은 쪽 무더기의 이동 비용이 더 적으므로, 자명하게 양이 많은 쪽으로 몰아넣어야 합니다.

정리하자면, 각 위치의 잔해는 마치 한 덩어리인 것처럼 취급해도 최적 비용에 영향이 없고, 기존에 잔해가 있던 위치 중 한 곳으로 몰아넣는 것은 최적 비용에 영향이 없거나 또는 그렇게 해야만 최적이 됩니다.

이제 최적 비용을 구하는 것을 생각해봅시다. 이동 거리의 폭도 넓고 비용 $T$의 범위도 넓습니다. 마냥 크기가 작은 잔해를 큰 쪽으로 붙인다고해서 최적의 비용이 나오지는 않습니다. $T$와 잔해의 위치에 따라서 최적해가 달라집니다. 애초에 몇 개의 무더기를 만들지도 모르는 상황에서 그리디하게 몰아넣는 것으로는 답을 구할 수가 없습니다.

그리디로는 안 된다면 생각해볼 수 있는 방법은 역시 다이나믹 프로그래밍이네요. DP를 풀 때는 항상 점화식을 잘 세우는 것이 관건입니다. 다음 두 가지 경우를 고려해보죠.

현재 잔해를 옮기는 것이 최적일 때
현재 잔해 위치에 무더기를 만드는 것이 최적일 때

이제 편의상 $dp_{i,0}$를 현 위치가 무더기가 아닐 때의 최소 비용, $dp_{i,1}$를 현 위치가 무더기일 때의 최소 비용이라 하겠습니다. 그리고 $dp_i = min(dp_{i,0},dp_{i,1})$이라 하겠습니다. 둘 중 더 작은 값을 취하겠다는 뜻입니다. 이제 왼쪽 잔해부터 시작해 오른쪽으로 훑어가며 최소 비용을 구해나갈 겁니다.

현재 잔해를 움직이지 않을 때의 최소 비용 $dp_{i,1}$를 구해봅시다. 이 과정은 자신보다 왼쪽에 있는 잔해들을 오른쪽으로 끌어모으면서 값을 구해나갑니다.

dp1

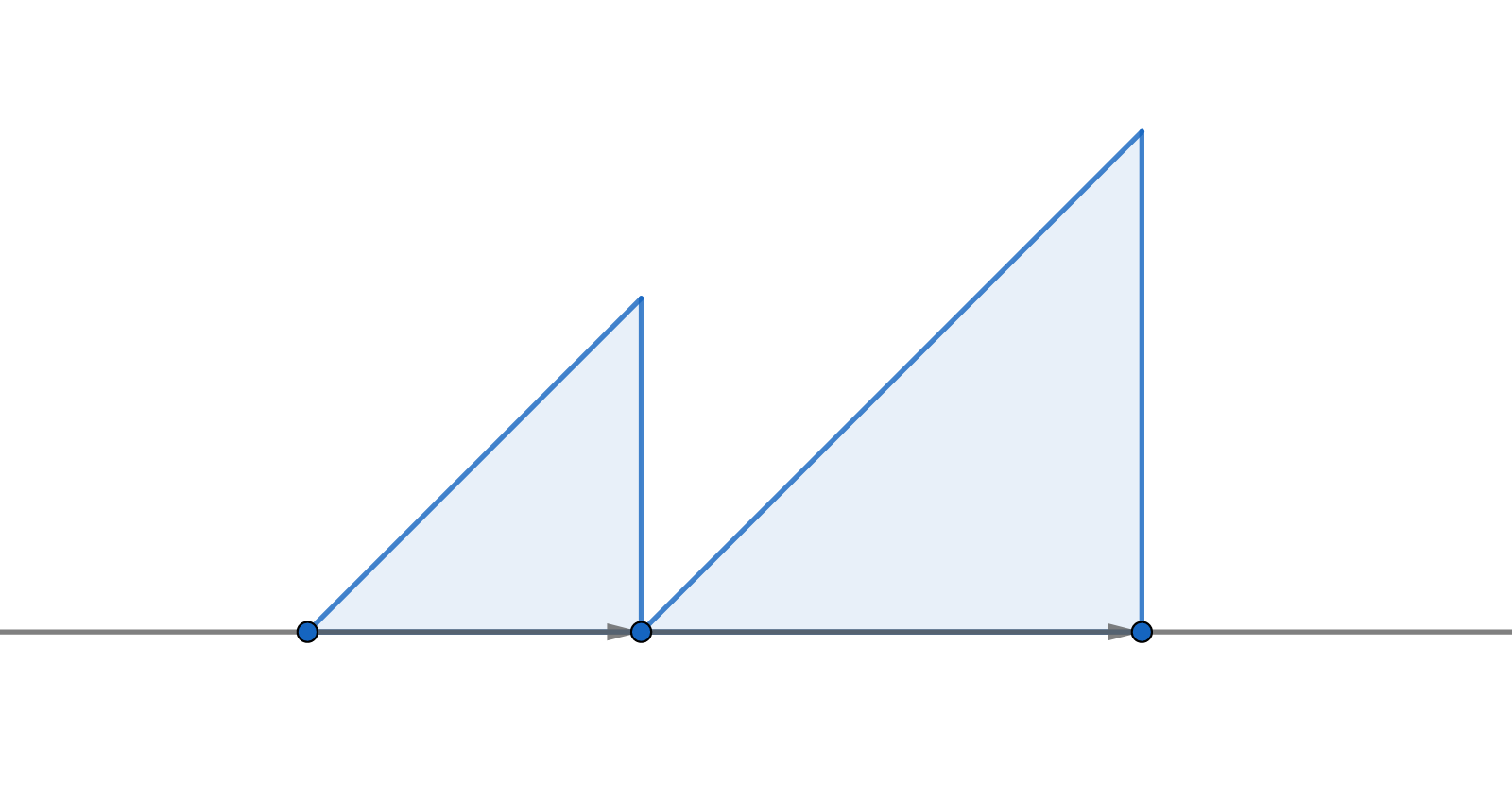
일단 $dp_{0,1}=T$입니다. 그리고 $0$보다 큰 $i$에 대해서는, $j < i$인 모든 $j$에 대해 다음 식으로 구해줍니다.

$$ dp_{i,1}=\min(dp_{j-1}+cost(j,i)+T) $$

dp3

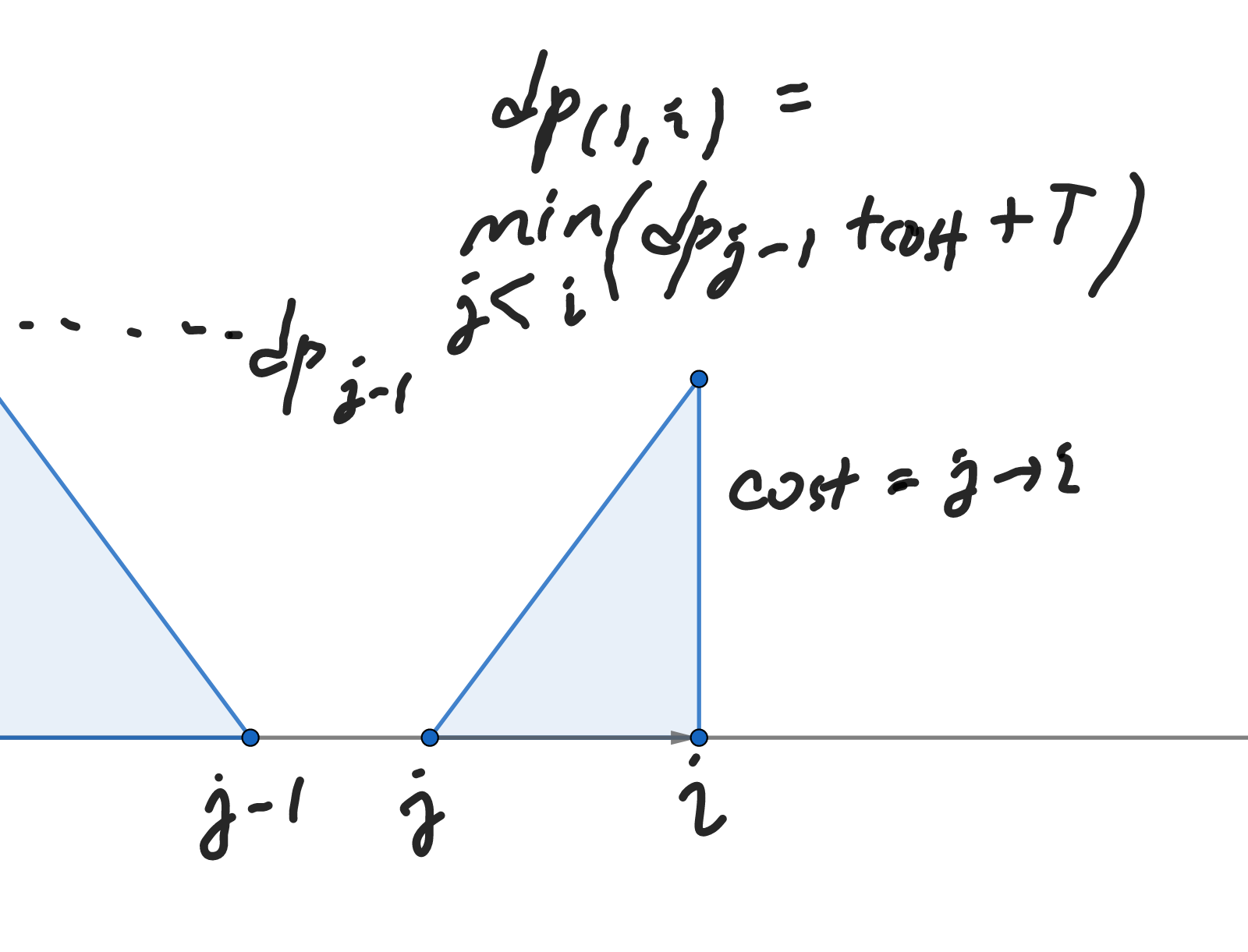
$cost(j,i)$는 $j$번째 잔해부터 모두 밀어서 $i$ 위치까지 모았을 때의 비용입니다. 이 비용과 $j-1$까지의 최소 비용을 더하는 겁니다.

이제 지금 보고 있는 잔해 $i$를 옮겨야 한다고 합시다. 이 때 왼쪽에 있는 잔해들의 지점에서의 최소 비용은 모두 구해져 있으므로 왼쪽으로 옮겨가면서 최소 비용을 갱신해 나갈 겁니다.

dp0

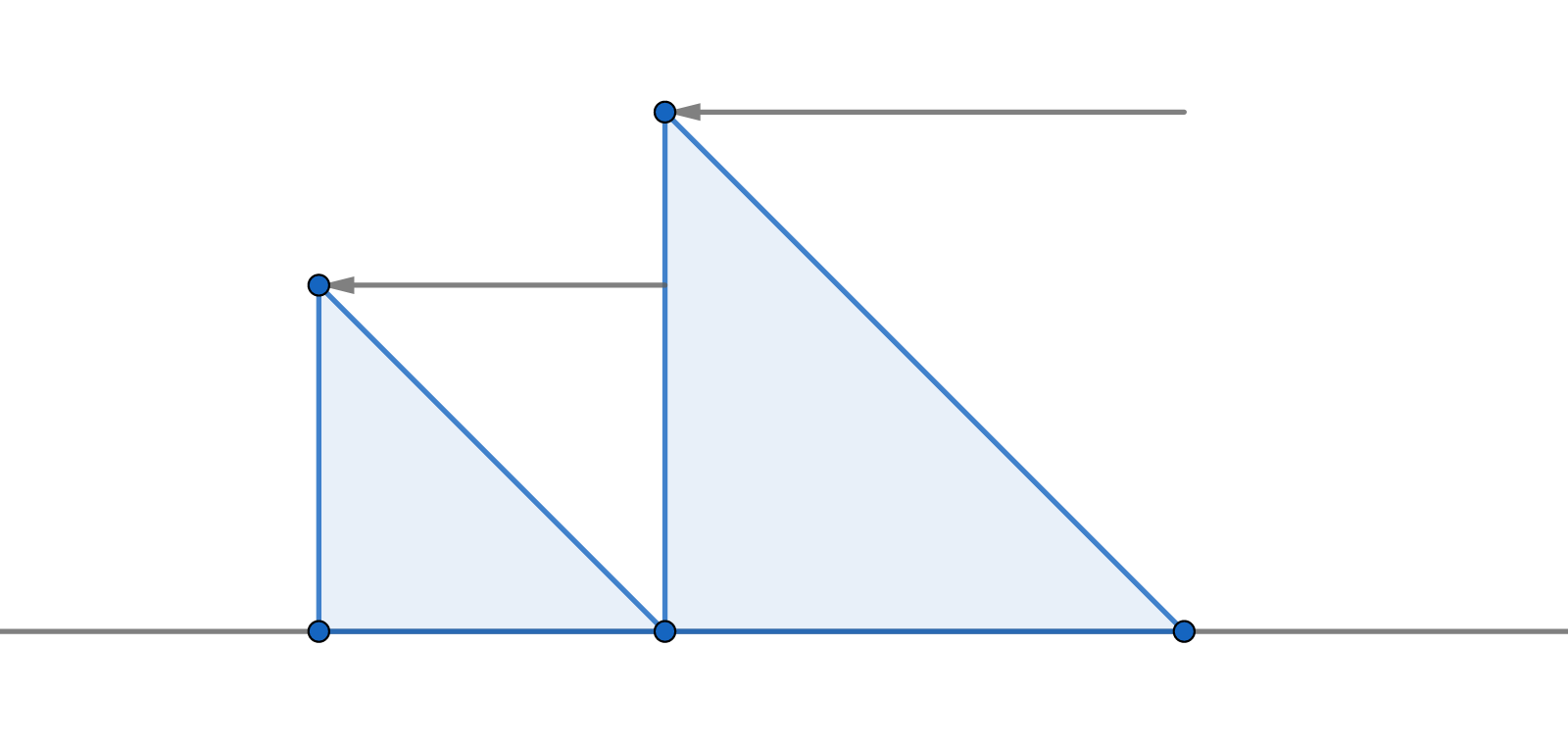
그렇다면 $dp_{i,0}$를 구하기 위해서는 다음 식을 구하면 됩니다.

$$ dp_{i,0}=\min(dp_{j,1}+cost(i,j)) $$

dp2

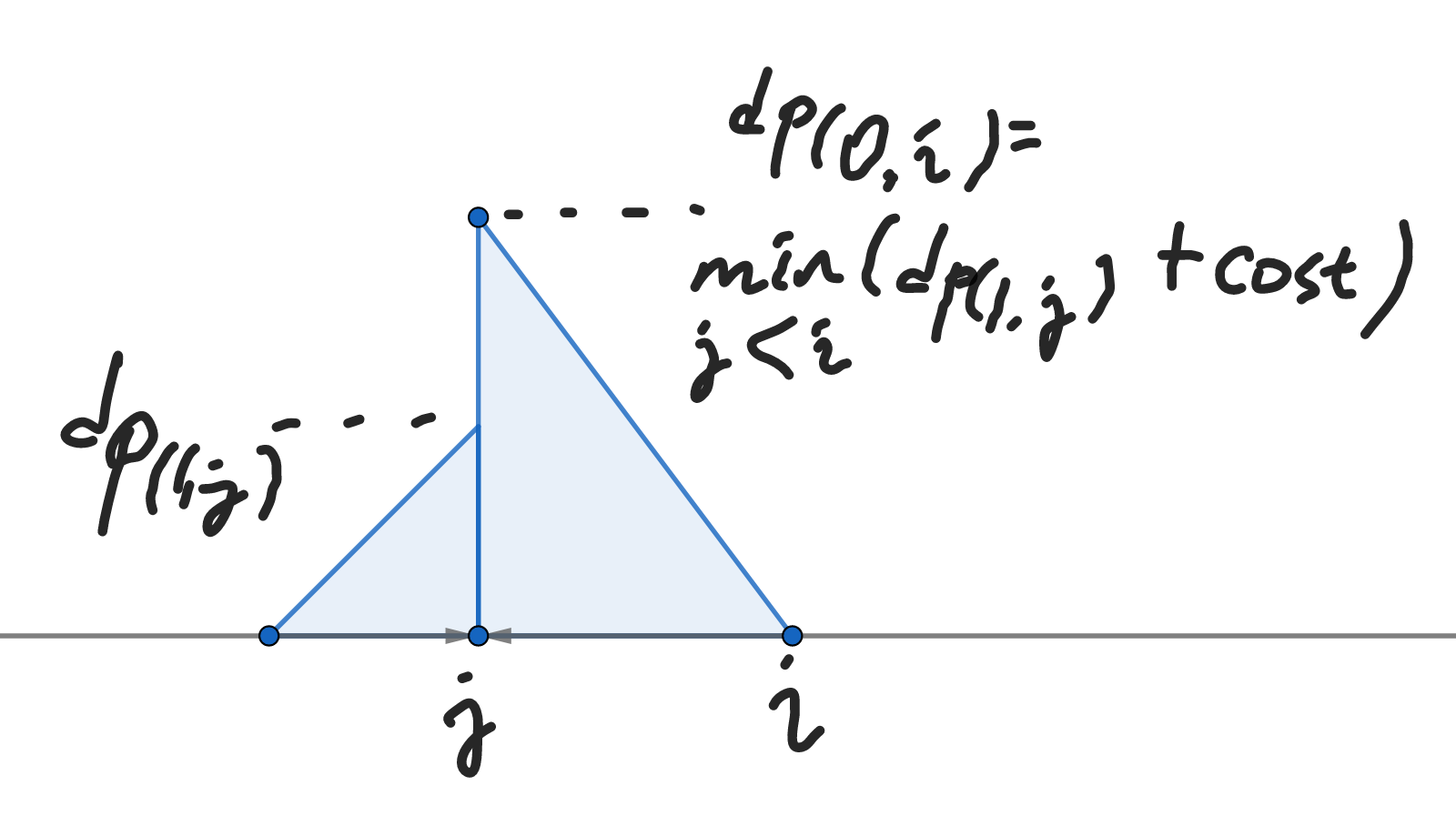
$dp_1$을 구할 때와는 조금 식이 달라집니다. 일단 왼쪽으로 밀어넣을 위치는 무더기가 있어야 합니다. 비용 $T$를 이미 포함하고 있는 값인 $dp_{j,1}$을 쓰지 않으면 제대로 된 값이 나오지 않습니다. $cost(i,j)$ 또한 아까와는 반대 방향으로 $i$번째 잔해부터 모두 밀어서 $j$ 위치까지 모았을 때의 비용입니다.

두 점화식을 각각 구해나가다보면 양쪽에서 모은 무더기의 최적 비용까지 모두 고려할 수 있게 됩니다. 머릿속에 그려지시나요?

이제 관건은 시간복잡도입니다. 사실상 일차원 DP가 되었지만, 내부적으로 계산해야 할 값이 많습니다. DP의 각 위치 $i$에서의 값을 구하기 위해서는 $j < i$를 모두 고려해주어야 합니다. 또한 각 $j$에 대해서도 구간에 대한 누적합인 $cost(i,j)$를 계산해야 하므로 $O(N^3)$이 될 것 같습니다. 하지만 누적합을 미리 계산해둔다든지, $dp$의 값을 갱신해 나가는 방향을 적당히 조작하면 $cost$를 구하는 시간을 $O(1)$로 만드는 것이 가능합니다. 그리 특별할 것 없는 테크닉으로 충분히 시간복잡도를 한 차원 낮출 수 있습니다.

typedef long long ll;
const int LEN = 201;

int K, N, T, A[LEN], D[LEN];
ll dp[LEN][2], ret[LEN];

ll solve() {
	std::cin >> N >> T;
	for (int i = 1; i <= N; ++i) std::cin >> D[i] >> A[i];
	dp[0][1] = T;
	for (int i = 1; i <= N; ++i) { // 잔해의 위치 i를 왼쪽부터 오른쪽으로 훑습니다
		dp[i][0] = dp[i][1] = ret[i - 1] + T; // 초기화: T를 더하여 최대값으로 만들어줍니다
		ll cost = 0, S = 0;
		for (int j = i; j > 0; --j) { // 왼쪽으로 밀어가면서 비용을 계산해나갑니다
			cost += (S += A[j]) * (D[j] - D[j - 1]); // 왼쪽으로 밀어 합치는 비용을 O(1)로 계산합니다
			dp[i][0] = std::min(dp[i][0], dp[j - 1][1] + cost); // 위에서 설명한 점화식과 같습니다
		}
		cost = 0, S = 0;
		for (int j = i - 1; j > 0; --j) { // 오른쪽으로 당겨오는 비용을 계산합니다
			cost += (ll)A[j] * (D[i] - D[j]); // 이것 또한 누적합을 O(1)로 계산합니다
			dp[i][1] = std::min(dp[i][1], ret[j - 1] + cost + T); // 위에서 설명한 점화식과 같습니다
		}
		ret[i] = std::min(dp[i][0], dp[i][1]);
	}
	return ret[N];
}

이것보다 깔끔한 풀이가 있을 것 같긴 한데, 일단 포스팅해봅니다.

Categories