백준 16181 - Coloring Roads

스플레이 트리를 응용하는 자료구조로, 트리를 동적으로 관리하면서 구간 쿼리를 빠르게 처리하는 링크/컷 트리를 공부했습니다. 이번엔 링크/컷 트리의 연산을 특이하게 응용해서 Coloring Roads를 풀어봤습니다. 원래 에디토리얼에 있는 정해는 분할상환 시간복잡도에 대한 깊은 이해가 있어야 하지만, 이 풀이를 따르면 시간복잡도에 대한 증명은 자료구조에 넘기고 순전히 구현에만 신경쓸 수 있게 됩니다.

문제는 단순합니다. 트리 상의 임의의 정점에서 루트까지 올라가면서 거치는 모든 간선을 한 가지 색깔로 칠하고, 각 색깔이 몇 개 칠해지는지를 구하면 됩니다. 물론 정말 단순하게 풀 수 있었다면 HLD나 링크/컷 트리를 쓸 일도 없겠죠. 정점과 쿼리가 각각 \(200,000\)까지이므로 나이브한 풀이로는 어림도 없습니다. 하지만 링크/컷 트리의 access 연산이 이루어지는 동안 트리의 형태가 어떻게 변해가는지를 깊게 이해하고 있다면, 이 문제는 아이러니하게도 그냥 access 연산을 이십 만 번 하면 되는 것으로 바뀌게 됩니다. 물론 이 문제는 트리의 형태가 바뀌지 않습니다. 또한 스스로도 하위 개념으로 풀 수 있는 문제에 상위 개념을 끌어들이는 것을 그다지 좋아하지 않지만 가끔 증명이 귀찮거나 극도로 재밌거나 단순해지는 풀이가 존재하면 시도해보기도 합니다.

링크/컷 트리가 어떤 자료구조인지는 검색만 하면 질 좋은 자료를 많이 찾아볼 수 있습니다. 이번 글에서는 풀이에 필요한 부분을 설명하는 데에 초점을 둘 것이므로, 아직 HLD나 링크/컷 트리가 무엇인지 모른다면 먼저 찾아보신 후 읽는 것을 추천드립니다.

통상의 HLD에서 구간은 체인 형태로 관리됩니다. 체인의 꼭대기를 계속 따라가다보면 루트가 나오죠. HLD는 확실히 트리 상의 구간 쿼리를 빠르게 처리하는 좋은 기법이긴 하지만, 트리의 형태가 고정되어 있어야 한다는 제약이 따릅니다. 간선이 추가, 삭제되면 세그먼트 트리 상에서의 업데이트 구간이 뒤틀리게 되죠. 동적으로 형태가 바뀌는 트리 상에서의 구간 쿼리를 위한 자료구조가 바로 링크/컷 트리입니다. 기본적인 아이디어는 HLD의 체인을 균형 이진 트리로 관리하겠다는 것입니다. 이를 위한 구조로 레드 블랙 트리를 쓰는 탱고 트리도 있지만 저는 좀 더 단순하게 스플레이 트리를 쓰는 쪽을 선택했습니다.

---

Access?

링크/컷 트리에서 access 연산은 임의의 정점을 splay하여 트리의 꼭대기까지 끌어올리는 것을 뜻합니다.

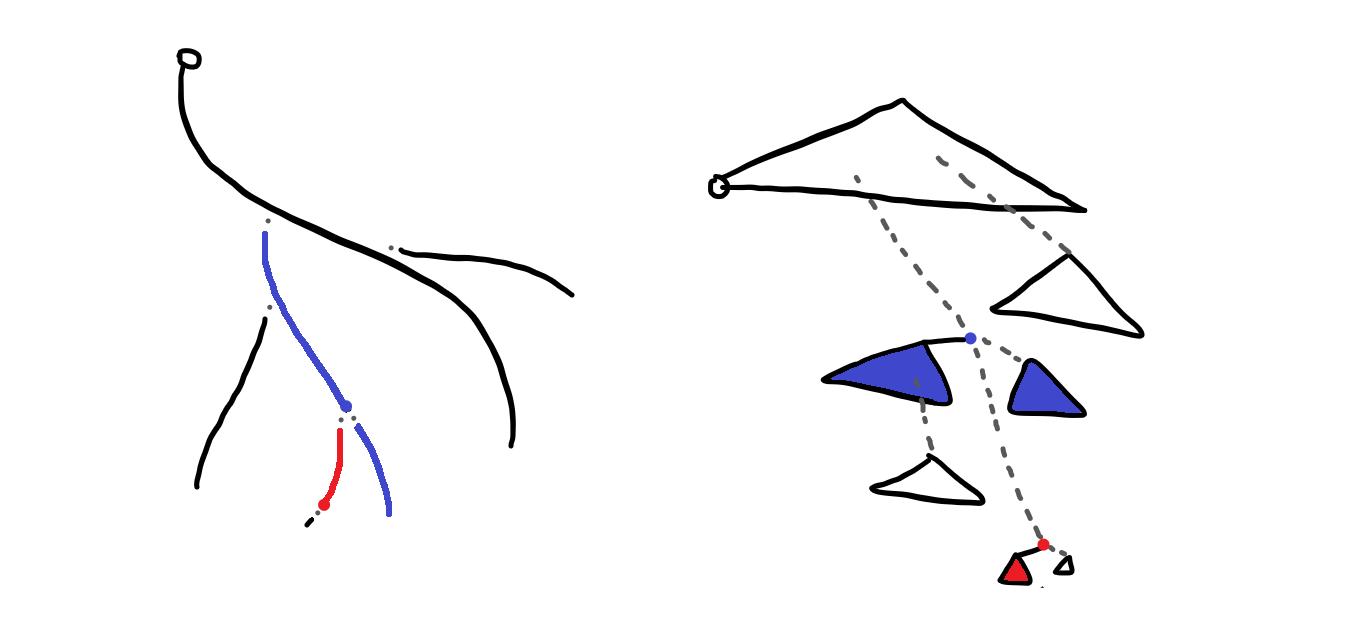
링크/컷 트리는 이렇게 생겼습니다. 왼쪽이 실제 트리고, 오른쪽이 체인으로 분리되어 있는 링크/컷 트리입니다. 여기서 용어를 짚고 넘어가겠습니다. 검은 선으로 연결된 정점들은 현재까지는 체인으로 연결된 경로이며, 이를 preferred path라 하겠습니다. 오른쪽 그림에선 삼각형으로 표현되어있고, 각각이 스플레이 트리로 되어있습니다. 회색 점선은 현 단계에서는 체인이 아닌 경로들을 의미합니다. 이를 auxilary path라 하겠습니다. 회색 점선들 또한 실제 트리에서는 양방향 간선입니다만, 링크/컷 트리에서는 자식에서 부모로만 향하는 방향 있는 간선이 됩니다. 이제 빨간 정점에 access 해보겠습니다.

스플레이 트리를 쓰는 링크/컷 트리에서 모든 연산의 핵심은 당연하게도 splay입니다. 일단 빨간 정점을 끌어올려줍니다. 그리고 빨간 정점의 오른쪽 연결을 끊습니다. auxilary path로 만들어서 빨간 정점 밑의 chain은 떨어져 나가게 됩니다.

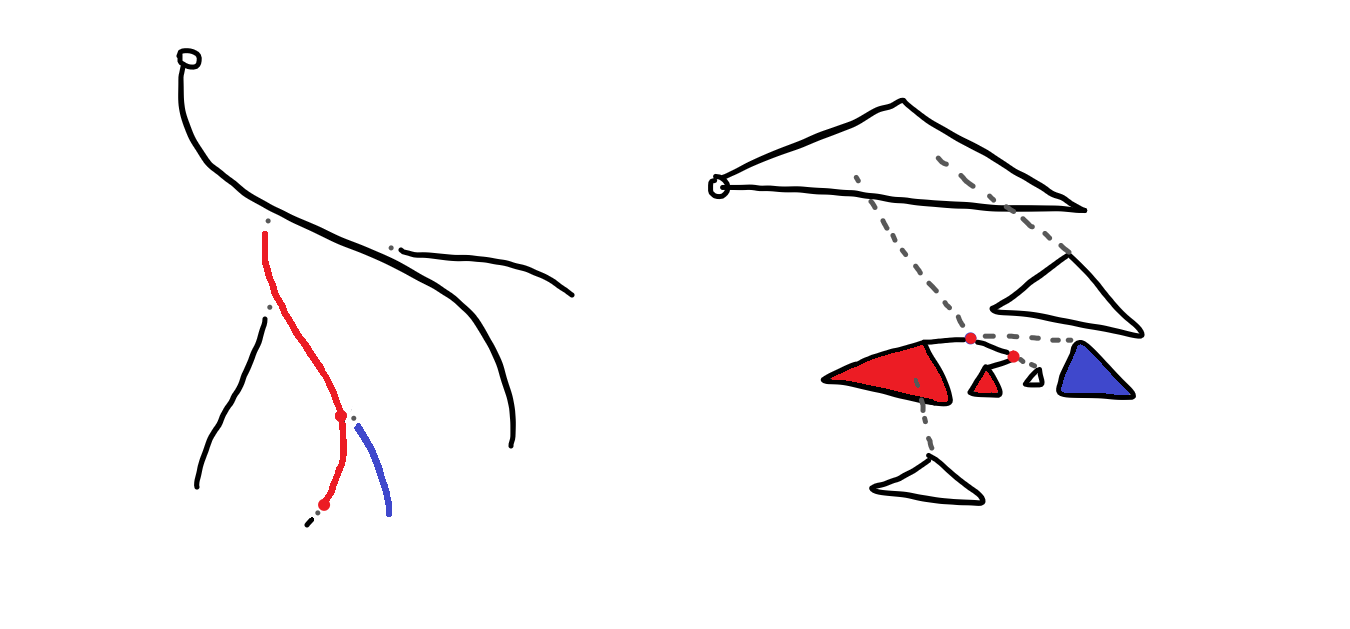
빨간 정점이 현재 체인에서는 splay하여 루트가 되었지만, 아직 access하지는 못하고 있습니다. 링크/컷 트리 상에서 빨간 정점의 부모가 되는 체인을 적당히 끊고 합쳐주어야 합니다. 일단 현재 빨간 정점의 부모를 splay 하고, 오른쪽의 연결을 마찬가지로 끊어줍니다.

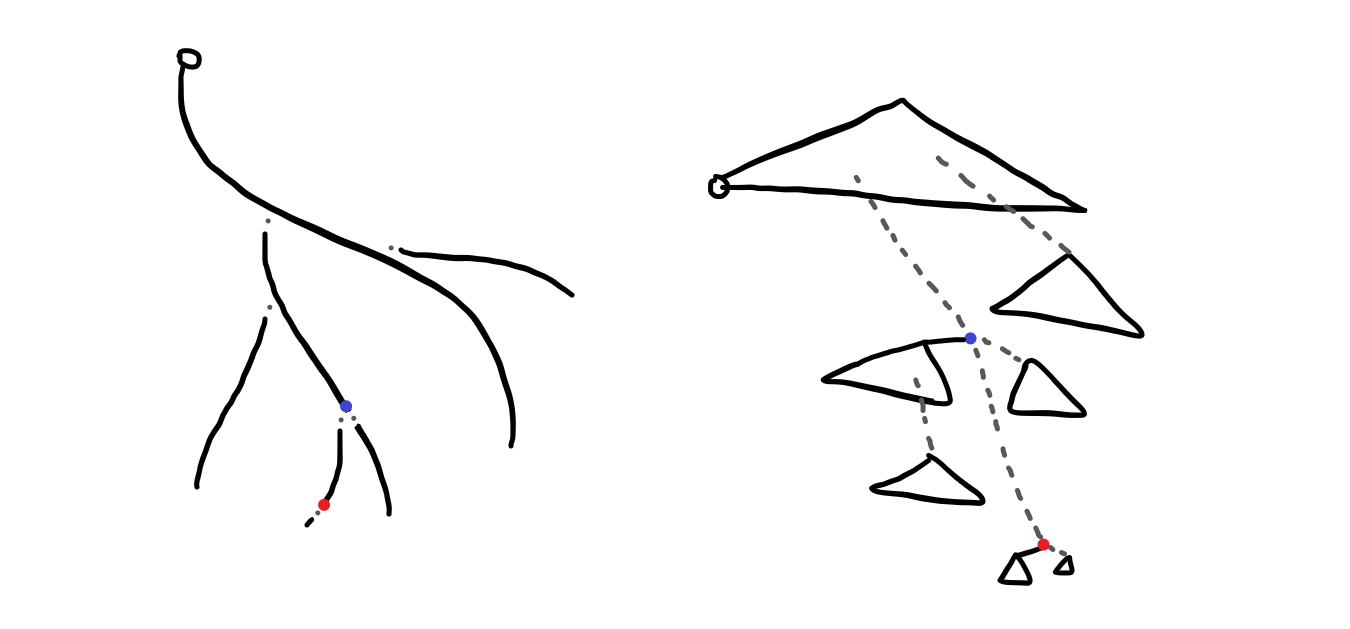
이제 두 스플레이 트리를 합쳐줍니다. 이 과정을 빨간 정점이 링크/컷 트리 상의 루트가 될 때까지 반복합니다.

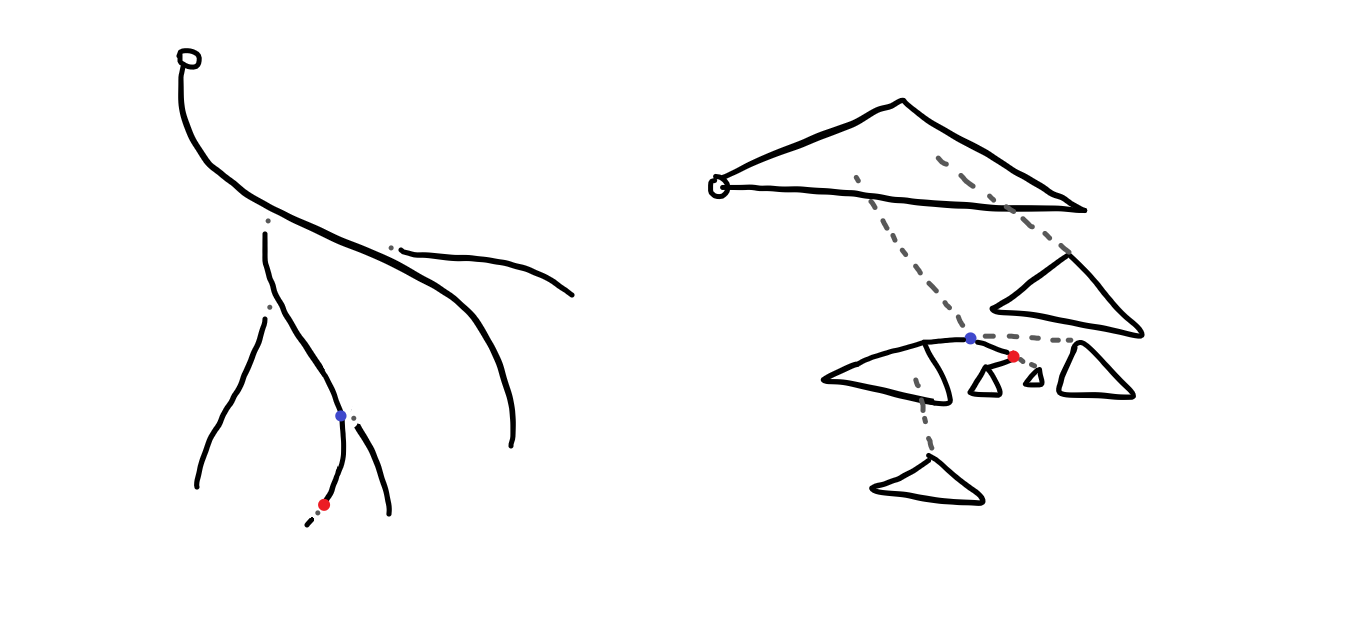
빨간 정점이 항상 루트에 있도록 splay합니다.

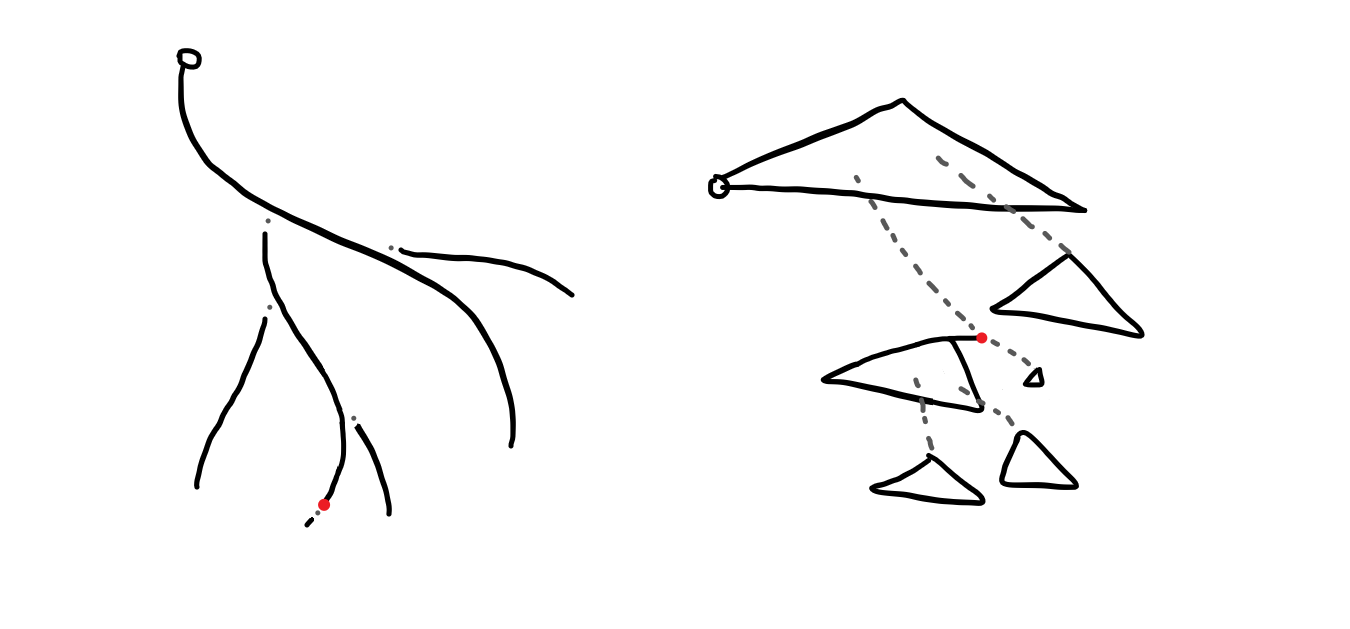
부모 정점을 splay합니다.

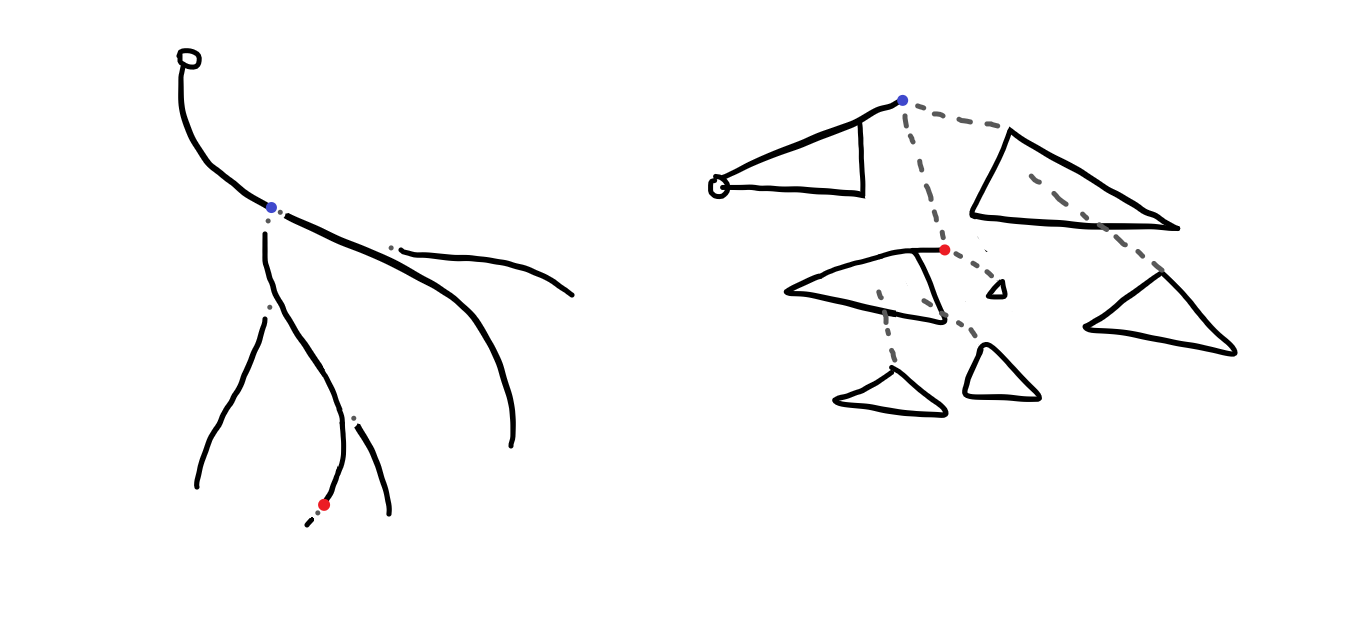
마찬가지로 두 스플레이 트리를 합쳐주고 빨간 정점이 루트가 되도록 해줍니다.

void access(Node* x) {
	splay(x); x->r = 0; // 1. 목표 정점을 splay, 오른쪽을 끊습니다.
	for (; x->p; splay(x)) // 2. 목표 정점이 루트가 될 때까지
		splay(x->p), x->p->r = x; // 3. 목표의 부모 정점을 splay한 후 트리를 합칩니다.
}

여기서 짚고 넘어갈 점은, 임의의 정점에 access했다고 해서 실제 트리에서의 루트가 되지는 않는다는 것입니다. 실제 트리 상에서의 위치는 그대로 유지한 채, 루트까지 도달하는 경로를 체인으로 모아줍니다. 이 과정을 통해 새로운 검은 실선-preferred path-이 만들어집니다. 그리고 이번 문제에서의 핵심은 바로 이 검은 실선을 한 가지 색깔로 칠해주는 것입니다.

Counting Colors

access 연산을 통해 트리가 만들어지면, 이 트리의 크기가 바로 새롭게 칠해지는 경로의 개수가 됩니다. 그렇다면 덮이면서 사라지는 색깔의 개수는 어떻게 알 수 있을까요? 이건 의외로 단순합니다. 부모 정점을 splay할 때, 바로 전 단계까지는 한 가지 색깔로 칠해져 있던 경로가 끊기면서, 오른쪽 트리는 기존의 색이 유지되고, 왼쪽 트리는 새로운 색깔이 칠해지게 됩니다. 매번 splay할 때마다 왼쪽 트리의 크기를 원래 색깔에서 빼주면 됩니다.

struct Node {
	Node* l, * r, * p;
	int s; // size
	int i;
	int c;
	void update() {
			s = 1;
			if (l) s += l->s;
			if (r) s += r->s;
		}
	bool is_root() { return !p || (p->l != this && p->r != this); }
	bool is_left() { return p->l == this; }
	int chain_size() { return 1 + (l ? l->s : 0); } // preferred path의 체인 길이는 왼쪽 트리의 크기
	void rotate();
} t[LEN];

int cc[LEN]; // count of colors: 특정 개수로 칠해져 있는 색깔의 개수를 저장합니다.
int c[LEN]; // color: 특정 색깔이 몇 개 칠해져있는지를 저장합니다.

...

void get_color(int u, int v) { // u: 목표 정점, v: 새로 칠할 색
	Node* x = &t[u]; // x는 목표 정점의 링크/컷 트리 노드

	splay(x); x->r = 0; x->update(); // access 연산의 1번 단계
	if (x->c) { // 목표 정점에 원래 색이 칠해져 있었다면
		--cc[c[x->c]]; // 기존 색깔 c로 칠해져 있던 개수가 하나 줄어듭니다.
		c[x->c] -= x->chain_size() - (x->p == 0); // 왼쪽 트리의 개수만큼 개수가 줄어들고
		++cc[c[x->c]]; // cc를 업데이트합니다.
	}
	for (; x->p; splay(x)) { // access 연산의 2번 단계
		splay(x->p); // access 연산의 3번 단계. 부모 정점을 끌어올립니다.

		if (x->p->c) {
			--cc[c[x->p->c]];
			c[x->p->c] -= x->p->chain_size() - (x->p->p == 0);// 왼쪽 트리의 개수만큼 개수를 줄입니다.
			++cc[c[x->p->c]];
		}

		x->p->r = x; // 두 트리를 합치고 x가 루트가 될 때까지 반복합니다.
	}
	--cc[c[v]];
	c[v] += x->s - 1; // preferred path가 완성되었습니다. 트리의 크기만큼 색깔 개수가 늘어납니다.
	++cc[c[v]];
}

위 get_color 메서드는 access와 동일한 시간복잡도를 가집니다. 문제에서 요구하는 쿼리를 빠르게 처리할 수 있는 것이죠. 하지만 여기까지만 만들어서는 반쪽짜리에 불과합니다. 현재까지의 색깔의 개수는 빠르게 알 수 있지만, 새로운 색으로 칠하는 과정이 없기 때문입니다.

Lazy propagation과 Coloring

쿼리를 수행할 때마다 모든 노드의 색을 바꿔주는 건 너무 느립니다. 하지만 스플레이 트리의 Lazy propagation을 이용하면 색을 칠하는 것을 최대한 뒤로 미룰 수 있죠. 체인이 된 스플레이 트리의 루트에 페인트를 왕창 칠해놓고 자식이 위로 올라갈 때 스치면서 색이 칠해지게 하는 것입니다.

struct Node {
	Node* l, * r, * p;
	int s; // size
	int i;
	int c, lazy; // c는 노드의 색깔, lazy는 체인에 칠해야 하는 색깔
	void push() {
		if (lazy) {
			c = lazy;
			if (l) l->lazy = lazy;
			if (r) r->lazy = lazy;
			lazy = 0;
		}
	}
	...
	void splay(Node* x) {
		for (Node* p; !x->is_root(); x->rotate()) {
			p = x->p;
			if (!p->is_root()) p->p->push(); p->push(); x->push(); // 자식을 체인의 색깔로 칠합니다
			if (p->is_root()) continue;	// zig
			if (x->is_left() == p->is_left()) p->rotate();	// zig-zig
			else x->rotate();	// zig-zag
		}
		x->push();
	}
} t[LEN];

이제 splay를 하는 시점까지 색칠하는 것을 최대한 뒤로 미룰 수 있게 되었습니다. 색깔의 개수를 구하는 것을 넘어 업데이트까지 할 수 있습니다.

void set_color(int u, int v) {
	Node* x = &t[u];

	splay(x); x->r = 0; x->update();
	if (x->c) { ... }
	for (; x->p; splay(x)) {
		splay(x->p);
		if (x->p->c) { ... }
		x->p->r = x;
	}
	...
	x->lazy = v; // 체인의 루트에 페인트를 왕창 뿌려줍시다.
}

모든 쿼리를 \(amortized O(Q \log N)\)으로 처리할 수 있게 되었습니다. 스플레이 트리의 시간복잡도 증명까지 해줘야 이 풀이가 완성되는데, 그건 나중에 포스팅해보도록 하죠.