백준 13576 - Prefix와 Suffix
문자열을 효율적으로 처리하는 알고리즘은 목적에 따라 다양합니다. 보통은 \(O(N^2)\)이 걸릴 작업을 평균 \(O(N\log N)\), 짧게는 \(O(N)\)으로도 해결할 수 있게 만듭니다. 예를 들어 패턴 매칭에 활용되는 KMP는 시간복잡도가 패턴 길이 \(|P|\)와 문자열 길이 \(|T|\)에 대해 \(O(|P|+|T|)\)입니다. 문자열 내에 존재하는 모든 회문을 검사하는 manachers는 문자열 길이 \(|S|\)에 대해 \(O(|S|)\)입니다. 무식하게 이런 문제들을 접근한다면 시간복잡도가 제곱이 되는 건 피할 수 없겠지만, 위에서 소개하는 문자열 알고리즘들은 미리 계산해둔 값들을 영리하게 활용하여 불필요하게 반복되는 연산을 최대한 없앱니다. 이번 문제를 풀면서 설명할 manber-myers 알고리즘과 lcp 또한 같습니다.
이번 문제는 Prefix와 Suffix입니다. 접두사, 접미사를 다루는 문제에서 우선 후보로 올려볼 녀석으로는 Trie 자료구조, KMP, Z 그리고 접미사 배열 등이 있습니다. 관건은 접두사인 동시에 접미사인 문자열이 최악일 때 문자열의 길이인 \(N\)개까지 존재하는데, 그 \(N\)개의 모든 접미사들에 대해 등장횟수를 구해야 한다는 겁니다. 그냥 KMP를 \(N\)번 돌리는 걸로는 택도 없겠죠. 이 문제를 해결하는 방법이 물론 하나만 있는 건 아니지만, 이 글에서는 lcp 배열로 접근하겠습니다.
접미사 배열
접미사 배열에 대해 다루는 글들은 찾아보면 많으니 자세히 적지는 않겠습니다. 간단히 설명하자면, 접미사 배열은 어떤 문자열의 모든 접미사들에 대해, 사전순으로 정렬해놓은 것을 말합니다.
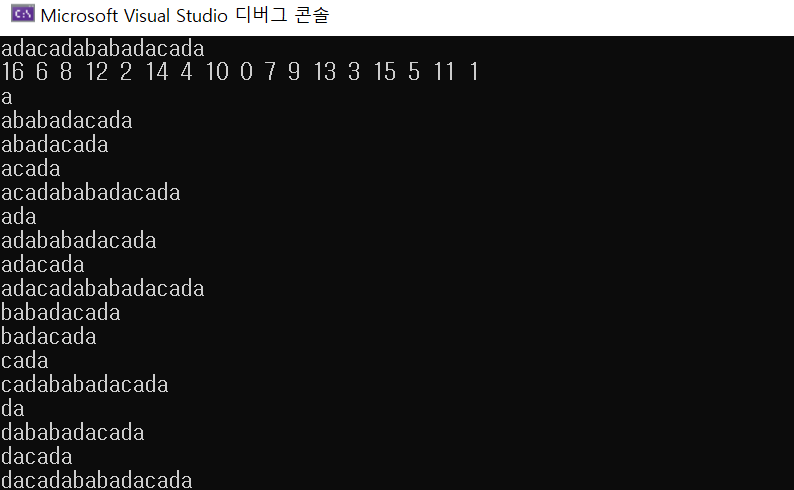
마음같아서는 \(0\)부터 \(N - 1\)까지의 모든 \(i\)에 대해 접미사를 문자열로 저장하고 sort 한번 돌려서 해결해버리고 싶지만, 짚고 넘어갈 부분이 꽤 있습니다.
- 정렬은 \(O(N \log N)\), 하지만 문자열이라면…
꽤 큰 크기의 데이터라도, 원소가 숫자라면 저장과 대소 비교가 그닥 비싸지는 않습니다. 아무리 커봐야 8바이트일 것이고, 대소 비교도 한 번이면 충분합니다. 하지만 문자열은 다릅니다. 길이 \(1\)부터 \(N\)까지의 모든 접미사를 저장하는 데 필요한 메모리는 \(N^2\)입니다. 문자열 간 사전순 비교의 평균 시간복잡도는 \(O(N)\)이고, 전체 정렬에 소모되는 시간은 \(O(N^2\log N)\)입니다. 공간도, 시간도 단순히 접근하기에는 무리가 있습니다. manber-myers 알고리즘은 접미사의 배열에 각 문자열의 시작 인덱스만을 넣어서 공간을 \(N\)으로 줄이고 미리 정렬해둔 결과들을 재활용하여 시간복잡도를 \(O(N \log^2 N)\), 짧게는 \(O(N \log N)\)까지 줄입니다. 이것이 어떻게 가능할까요? 아이디어는 다음과 같습니다.
\(2^k\)만큼 길이를 늘려가며 한 글자씩만 비교하면서 정렬하겠다!
확실히 한 글자씩만 비교하고, 2의 거듭제곱만큼 정렬한다면 시간복잡도는 \(O(N \log^2 N)\)이 될 것 같습니다. 이게 어떻게 유효한 방법이 되는지는 접미사 배열의 특성과 관련지어 생각해본다면 답을 찾을 수 있습니다.
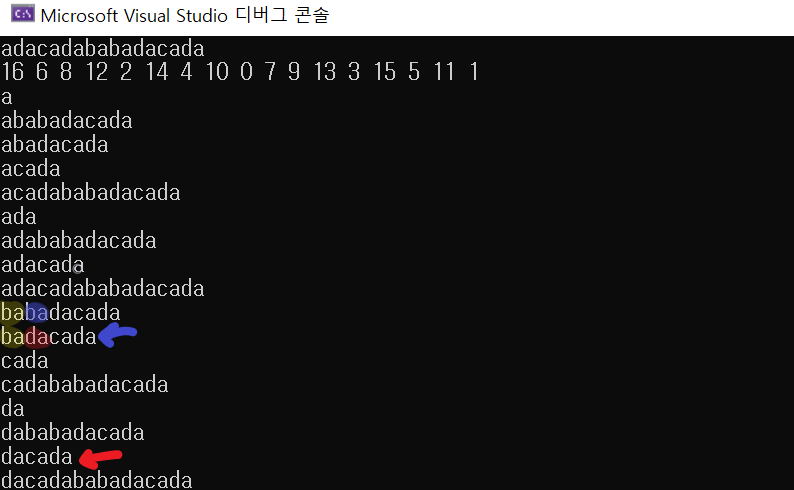
문자열의 1, 2, 4번째 글자를 비교하며 나아간다고 할 때, 사이에 있는 문자들을 뛰어넘으면 제대로 정렬이 될지 의심이 들 수도 있습니다. 그런데 여기서 중요한 점은 접미사 배열에서 자신의 접미사들은 모두 배열 안에 있다는 것입니다. 여기서 더 확장하자면 자신보다 더 짧은 접미사들에 대한 정렬은 완료되어 있다는 것은 어렵지 않게 생각해낼 수 있습니다. 미리 정렬해둔 결과들을 재사용해서 한 글자씩만 비교해서도 문자열의 사전순 정렬이 가능해집니다. 정렬은 통상의 비교 기반을 사용한다면 \(O(N \log N)\)이지만, \(N\)개 문자열의 순서만이 정렬 대상이므로 기수 정렬을 시행할 수 있습니다. 정렬에 소모되는 시간을 \(O(N)\)으로 만들어줄 수 있습니다.
int cnt[LEN], ord[LEN], SA[LEN], g[LEN], tg[LEN];
inline int min(int x, int y) { return x < y ? x : y; }
inline bool compare(int x, int y, int t) { return g[x] == g[y] ? g[x + t] < g[y + t] : g[x] < g[y]; }
void manber_myers(const int n, const char* s) {
for (int i = 0; i < n; ++i) SA[i] = i, g[i] = s[i];
for (int t = 1; t < n; t <<= 1) {
// radix sort by rank(i + 2^t)
memset(cnt, 0, sizeof cnt);
for (int i = 0; i < n; ++i) ++cnt[g[min(i + t, n)]];
for (int i = 1; i < LEN; ++i) cnt[i] += cnt[i - 1];
for (int i = n - 1; i >= 0; --i) ord[--cnt[g[min(i + t, n)]]] = i;
// 기수 정렬, 카운팅 정렬 등에서 stable하려면 n을 역순으로 돌아야 합니다
// radix sort by rank(i)
memset(cnt, 0, sizeof cnt);
for (int i = 0; i < n; ++i) ++cnt[g[i]];
for (int i = 1; i < LEN; ++i) cnt[i] += cnt[i - 1];
for (int i = n - 1; i >= 0; --i) SA[--cnt[g[ord[i]]]] = ord[i];
tg[SA[0]] = 1;
for (int i = 1; i < n; ++i)
tg[SA[i]] = tg[SA[i - 1]] + compare(SA[i - 1], SA[i], t);
for (int i = 0; i < n; ++i) g[i] = tg[i];
}
}
이렇게 얻어낸 접미사 배열은 사실 독립적으로는 잘 쓰이지 않고, lcp 배열을 빠르게 계산하는 데에 함께 쓰입니다.
LCP 배열
LCP는 Longest Common Prefix, 즉 최장 공통 접두사를 의미합니다. LCP 배열은 접미사 배열의 인접한 문자열 간 최장 공통 접두사들의 길이를 구해놓은 것을 말합니다. 이것도 단순하게 구하자면 앞뒤 문자열의 길이만큼 비교하므로 \(O(N^2)\)만큼 시간이 소모됩니다. 하지만 어떤 인접 접미사 간 최장 공통 접두사의 길이를 구했다면, 앞 글자를 뺀 다음 접미사들 간 최장 공통 접두사의 길이도 빠르게 구할 수 있습니다. 앞 글자를 뺀 다음 접미사는 그냥 인덱스를 1 더해주면 되니까 어렵지 않게 찾아줄 수 있습니다. 앞 글자를 뺀 다음 접미사를 빠르게 구하고 LCP 배열에서 접미사 순서에 해당하는 위치에 값을 넣기 위해서는 Suffix Array에서 각 인덱스를 담고 있는 것에 대한 역함수가 필요합니다. 그리고 나머지는 코드를 보는 것으로도 충분합니다.
int lcp[LEN], rank[LEN];
void get_lcp(const int n, const char* s) {
for (int i = 0; i < n; ++i) rank[SA[i]] = i; // rank는 SA와 역함수 관계
for (int i = 0, j, k, l = 0; i < n; ++i) {
if (k = rank[i]) {
j = SA[k - 1]; // 접미사 배열에서의 인접 문자열
while (s[i + l] == s[j + l]) ++l; // 이전에 구해둔 lcp의 길이부터 시작합니다
lcp[k] = l;
if (l) --l; // 다음 접미사를 확인하기 전에 앞 글자를 빼줍니다
}
}
}
이제 문제를 풀 준비는 모두 끝났습니다.
접미사 등장 횟수 구하기
한 가지 문제가 남는데, 모든 접미사의 등장 횟수를 빠르게 구해주는 것입니다. 접미사 배열과 LCP 배열은 이런 문제를 해결하는 데에 특화된 자료구조죠. 다음 그림을 보면 느낌이 확 올 겁니다.

접미사 자신보다 LCP 길이가 크거나 같을 때까지 접미사 배열을 찾아 내려가면, 이동한 길이가 바로 등장 횟수가 됩니다. 메모이제이션을 활용하면, 모든 접미사의 등장횟수를 \(O(N)\)으로 구해줄 수 있습니다. DP에 대한 힌트는 이 글을 참고했습니다.
int f(int i) {
int& ref = dp[i];
if (ref) return ref;
ref = 1;
for (int j = i + 1; j < N && lcp[j] >= N - SA[i]; ++j) {
int len = f(j);
ref += len;
j += len - 1;
}
return ref;
}
이제 남은 것은 접두사이자 접미사인 것을 모두 찾아주는 작업입니다. 접미사의 길이와 lcp의 길이가 같은 것을 모두 찾아주면 되겠지만, 소소한 반례에 주의해야 합니다.
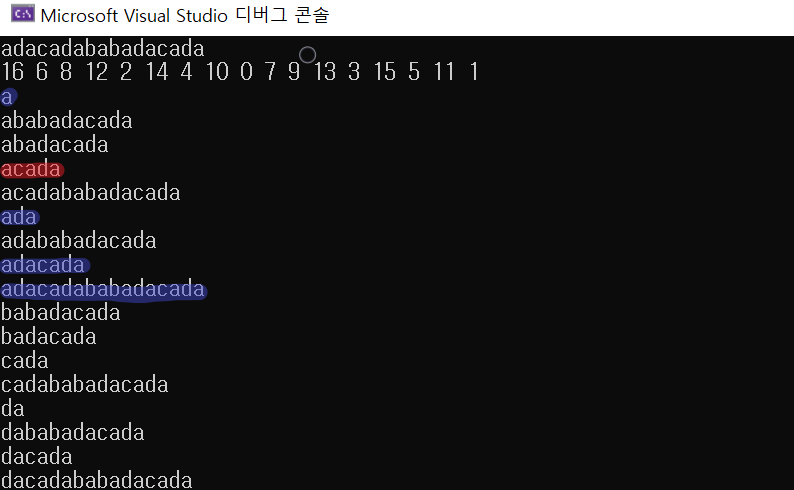
원본 문자열부터 시작하여 거슬러 올라가면서 접미사가 접두사와 같은 것을 찾아줍니다. 단, 접미사의 길이가 인접 접미사와의 공통 접두사 길이와 같다고 해서 접두사가 되는 것은 아닙니다. 이런 문제를 피하고 싶다면 KMP에서의 fail 함수를 써도 되지만, 접두사 길이를 갖고 있는 걸로도 문제 해결에는 충분합니다. 위로 올라갈수록 접두사의 길이는 짧아지므로 따로 정렬할 필요는 없습니다.
int sp, st[LEN];
for (int i = g[0] - 2, l = N; i >= 0 && lcp[i + 1]; --i) {
if (lcp[i + 1] <= l && N - SA[i] <= lcp[i + 1]) st[sp++] = i;
l = min(l, lcp[i + 1]);
}
이로써 문제가 해결됩니다.
접미사 배열과 관련해서는 접미사 트라이에 대한 이야기를 하고 넘어갈 필요가 있습니다. 좀 더 본질적인 것을 다루게 되는데, 저도 아직 이 부분은 완전히 이해한 것이 아니므로 자세히 적지는 않겠습니다. 잘 정리된 글이 있으니 링크를 달아두겠습니다.