백준 2844 - 자료구조

스플레이 트리에 푹 빠져있습니다. 취업도 생각해야하는데, PS가 공부해보면 또 재밌는게 많더군요. 스플레이 트리의 활용에 익숙해지면 풀 수 있는 문제를 찾았습니다. 그렇게 찾은 이번 문제는 자료구조입니다. 스플레이 트리의 코드는 Justice Hui 님의 블로그를 많이 참고했습니다.

이 문제에서 수행할 쿼리는 총 네 가지입니다.

\(A\)번째부터 \(B\)번째까지의 수를 \(X\)로 바꾼다.
\(A\)번째부터 \(B\)번째까지의 수에 \(X\)를 공차로 하는 등차수열을 더한다.
\(C\)번째 수 앞에 \(X\)를 넣는다.
\(A\)번째부터 \(B\)번째까지의 수의 합을 출력한다.

1, 2, 4번 쿼리만 있었다면 그냥 평범한 세그먼트 트리 문제가 되었을 텐데, 중간에 삽입 연산이 있습니다. 통상의 배열로 이 쿼리를 수행한다면 시간복잡도가 \(O(N)\)입니다. 그렇다고 연결리스트를 쓰자니 구간쿼리가 문제입니다. 구간합을 갖고 있으면서 빠르게 조회가 가능하고, 분할-삽입-병합을 빠르게 할 수 있는 그런 자료구조가 있을까요? 스플레이 트리라면 가능합니다! 물론 다른 자료구조도 찾아보면 쓸만한 건 많지만, 가장 단순한 것에서부터 출발하는 것도 좋겠죠.

스플레이 트리의 삽입

통상의 이진 검색 트리 삽입은 크기 순으로 비교해가면서 위치를 찾아 내려간 후 적절한 위치에 새 노드를 넣는 과정으로 이루어집니다.

binary_search

이진 검색 트리답게, 좌우로 왔다갔다 하며 적당한 위치를 찾습니다. 하지만 이 삽입 방식은 스플레이 트리가 이진 검색 트리의 성질을 가지고 있을 때 유효합니다. 구간 쿼리를 위한 각 위치의 원소 값을 가지고 있는 스플레이 트리에는 더이상 통상의 삽입 연산은 의미가 없죠.

이 문제에서 요구하는 것은 오히려 임의의 위치에 노드를 삽입하는 연산입니다. 스플레이 트리에서 임의의 노드를 끌어올리면-스플레이 하면-좌우 노드 개수는 변하지 않고 그대로 올라옵니다. 이진 검색 트리에서의 좌우 대소 관계가 유지되는 것입니다.

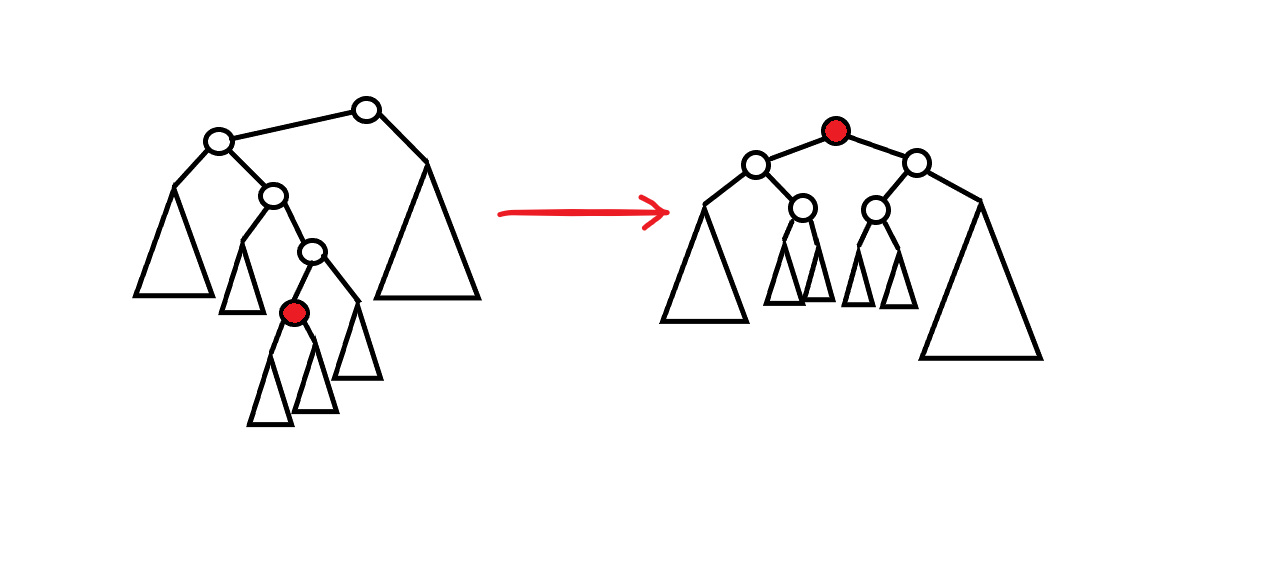
splay

임의의 \(K\)번째 원소를 찾는 연산은 각 노드마다 서브트리의 크기를 갖고 있도록 하면 \(O(\log N)\)으로 수행 가능합니다. 그렇다면, 스플레이 트리를 \(K\)번째 원소를 기준으로 자를 수 있게 되죠.

void get(int i) { // 0-base
	Node* p = root;
	if (!p) return;
	while (1) {
		while (p->l && p->l->size > i) // 왼쪽 트리의 크기가 i보다 크다면
			p = p->l; // 찾고자 하는 원소는 왼쪽 트리 밑에 있습니다.
		if (p->l) i -= p->l->size; // 왼쪽 트리의 크기가 i보다 작으면 넘어갑니다.
		if (!i--) break; // 찾는 위치에 도달
		p = p->r; // 오른쪽 서브 트리로 들어가서 다시 찾습니다.
	}
	splay(p); // 스플레이
}

split

\(K\)번째 원소를 splay한 후 앞이나 뒤를 자르고, 그 자리에 노드를 삽입할 수 있습니다. 보통의 링크드 리스트보다는 좀 느리지만, 배열에서의 삽입보다는 빠른 \(O(\log N)\)으로 임의의 위치 삽입이 가능해집니다.

void insert(int c, ll x) {
	get(c); // c번째 원소를 루트로 끌어올립니다.
	Node* r = root;
	Node* l = root->l; // c번째 원소의 왼쪽 서브 트리의 루트를 찾습니다.
	Node* m = new Node;
	m->val = x;
	m->l = l; l->p = m; // l-r 사이에 새로운 원소 m을 집어넣습니다.
	m->p = r; r->l = m;
}

그럼 이제 구간 쿼리를 처리해봅시다.

스플레이 트리의 구간 쿼리와 Lazy propagation

스플레이 트리의 가장 큰 특징은 임의의 노드가 구간을 갖도록 만들 수 있다는 것입니다. 저도 이 부분은 이해하기까지 꽤 오랜 시간이 걸렸습니다. 어떤 노드가 구간 \([S,E]\)를 갖도록 하려면 다음과 같이 만들어주면 됩니다.

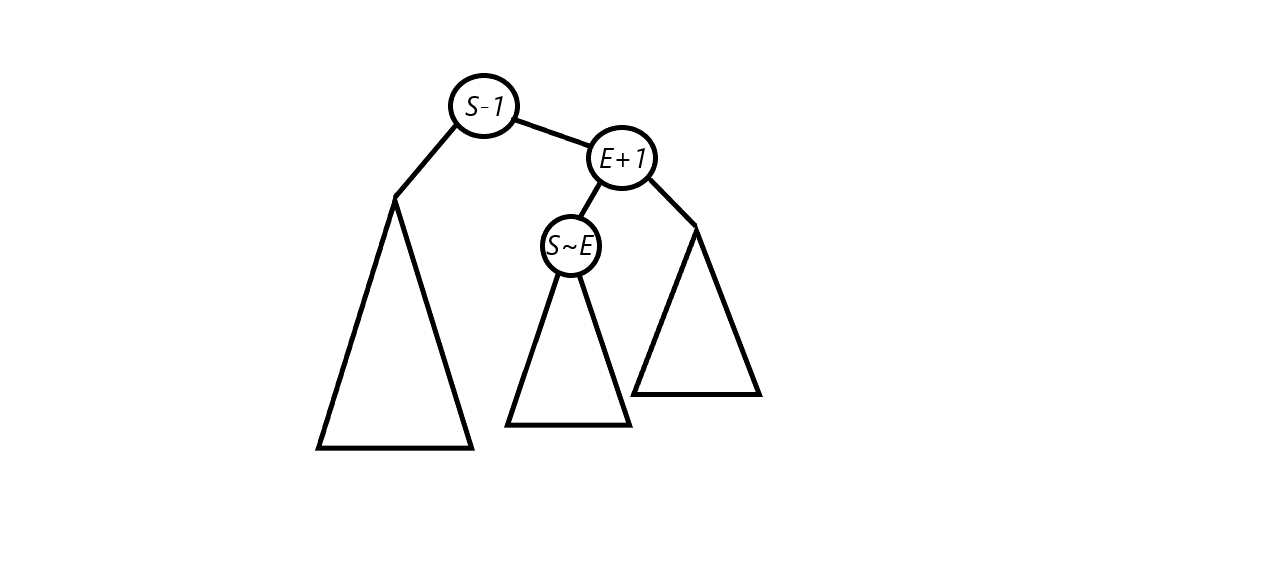
gather

우선 \(S-1\)번째 노드를 루트로 끌어올립니다. 그런 다음 \(E+1\)번째 노드가 루트의 오른쪽 밑에 바로 오도록 끌어올리면, \(E+1\)번째 노드의 왼쪽 밑에는 \([S,E]\)번 노드가 모입니다. 이제 타겟 노드에 구간 쿼리를 수행하기 위한 연산을 가해주기만 하면 됩니다.

우선 구간 노드의 루트에 늦은 갱신을 위한 변수들을 갖고 있게 합니다. 이후 검색, 스플레이 등 조회가 들어오거나 트리의 형태가 바뀔 때만 적당히 필요한 만큼만 갱신되도록 해줍니다.

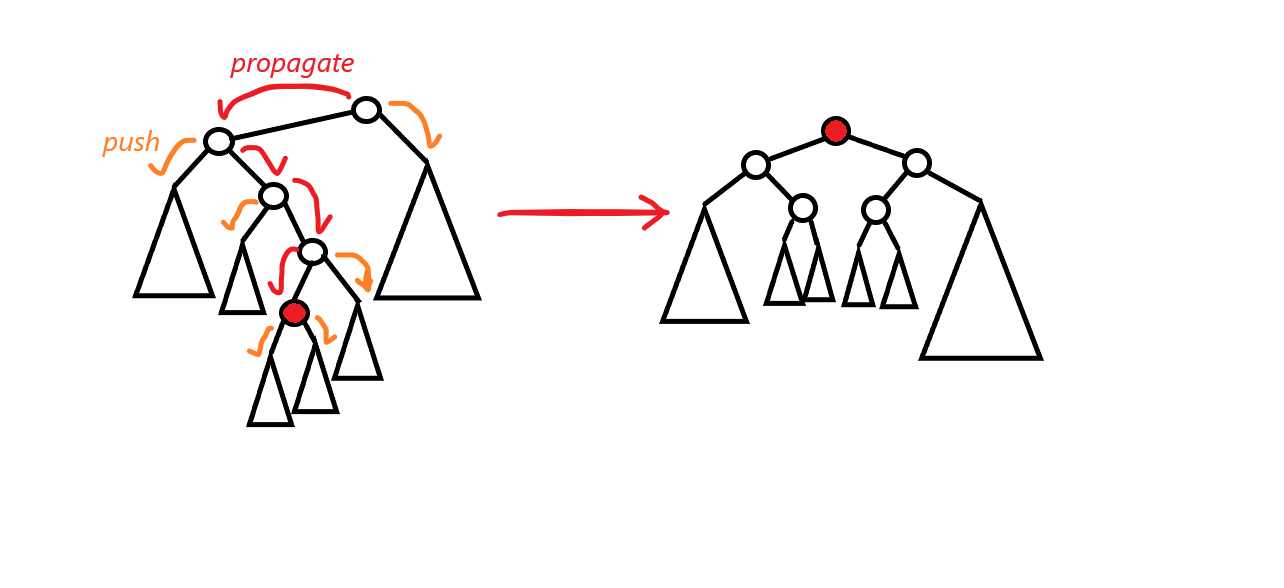
propagation

타겟 노드를 찾아 내려갈 때는 lazy propagation이 진행됩니다. 필요한 갱신값들을 자식 노드들에 push해줍니다. 타겟 노드를 끌어올리면서는 자식 노드들로부터 갱신된 정보를 pull합니다. 이 push-pull 연산이 적절히 이루어지도록 하는 게 스플레이 트리의 구간 쿼리에서의 관건이라 할 수 있습니다.

이제 문제를 풀기 위한 바탕이 되는 요소들은 알아보았습니다. 그럼 구간 쿼리를 구현해봅시다.

우선 보기에는 전혀 관계 없는 두 가지의 쿼리를 처리해야 하는 것처럼 보입니다. 구간의 숫자들을 특정 숫자로 바꾸거나, 아니면 등차수열을 더해야 합니다. Lazy propagation에서 두 가지의 독립된 쿼리로 하나의 변수를 조작하게 되면, 쿼리가 들어온 순서나 간격에 따라 값이 엉망진창으로 변합니다. 이 문제를 해결하기 위해 필요한 것은, 관계 없어보이는 두 쿼리를 하나의 식으로 합치는 일입니다.

조금 생각해보겠습니다. 구간의 숫자들을 \(X\)로 바꾸는 것은, 구간 전체에 0을 곱하고 초항 \(X\), 공차가 0인 등차수열을 더하는 것과 같습니다! 구간의 숫자들에 초항 0, 공차가 \(X\) 등차수열을 더할 때는 구간 전체에 1을 곱해주면 됩니다. 변수 3개로 두 쿼리를 한 가지 종류의 쿼리를 수행하는 것처럼 합쳤습니다.

부모 노드에서 자식 노드로 쿼리 정보(계수 \(x\), 초항 \(a_0\), 공차 \(d\))를 push할 때에는 다음과 같이 처리하면 됩니다.

void push(ll x, ll a0, ll d) { // x는 0 아니면 1
	this->x *= x; this->a0 *= x; this->d *= x; // x가 0이라면 지금껏 들어온 모든 갱신 정보를 초기화
	this->a0 += a0; this->d += d; // x가 1이면 기존의 등비수열에 새 등비수열을 더하는 것과 같습니다.
}

그리고 값이 실제로 평가될 때는 다음과 같이 됩니다.

void propagate() {
	if (!x || a0 || d) { // 갱신되어야 할 정보가 있다면
		int pivot = (l ? l->size : 0) + 1;
		val = val * x + a0 + d * pivot; // 현재 노드에 더해져야 할 값을 구합니다
		sum = sum * x + a0 * size + d * size * (size + 1) / 2; // 등차급수를 더합니다
		if (l) l->push(x, a0, d); // 자식 노드에 push
		if (r) r->push(x, a0 + d * pivot, d);
		x = 1; a0 = 0; d = 0; // 갱신이 이루어졌으므로 초기화
	}
}

더해져야 할 값과 등차급수는 등차수열의 성질을 이용해서 빠르게 구해줄 수 있습니다.

example

이제 구현만 적절히 해주면 됩니다.

#include <iostream>

typedef long long ll;

class SplayTree {
	struct Node {
		Node* l; // 왼쪽 자식
		Node* r; // 오른쪽 자식
		Node* p; // 부모 노드
		int size; // i번째 원소를 찾기 위한 서브트리 크기 변수
		ll val, sum; // 현재 노드의 값, 구간합
		ll x, a0, d; // eff, a0, diff
		Node() : l(0), r(0), p(0), size(1), val(0), sum(0), x(-1), a0(0), d(0) {}
		~Node() { if (l) delete l; if (r) delete r; }
		void push(ll x, ll a0, ll d) { // push. 실제로 값이 바뀌지 않음에 주의합니다.
			this->x &= x; this->a0 &= x; this->d &= x; // 0 또는 1을 곱하는 것은 비트 연산으로 바꿨습니다.
			this->a0 += a0; this->d += d;
		}
		void propagate() { // propagate. 특정 노드에서 실제 값이 갱신되는 것은 이 메서드의 호출 시점입니다.
			if (~x || a0 || d) {
				int pivot = (l ? l->size : 0) + 1;
				val = (val & x) + a0 + d * pivot;
				sum = (sum & x) + a0 * size + d * size * (size + 1) / 2;
				if (l) l->push(x, a0, d); // push. 갱신은 이루어지지 않습니다.
				if (r) r->push(x, a0 + d * pivot, d);
				x = -1; a0 = 0; d = 0;
			}
		}
		void update() { // pull 
			size = 1;
			sum = val;
			if (l) {
				l->propagate(); // 구간합 갱신
				size += l->size; // 왼쪽 트리의 크기를 더해 올립니다.
				sum += l->sum; // 왼쪽 구간의 합을 더해 올립니다.
			}
			if (r) {
				r->propagate(); // 구간합 갱신
				size += r->size; // 오른쪽 트리의 크기를 더해 올립니다.
				sum += r->sum; // 오른쪽 구간의 합을 더해 올립니다.
			}
		}
	} *root;
	void rotate(Node* x) {
		if (!x->p) return;
		Node* p = x->p;
		Node* b = 0;
		if (x == p->l) {
			p->l = b = x->r;
			x->r = p;
		}
		else {
			p->r = b = x->l;
			x->l = p;
		}
		x->p = p->p;
		p->p = x;
		if (b) b->p = p;
		(x->p ? p == x->p->l ? x->p->l : x->p->r : root) = x;
		p->update(); // 트리의 형태가 변화하였으므로 구간 정보를 pull 합니다.
		x->update();
	}
	void splay(Node* x, Node* g = 0) { // 타겟 노드 x가 g의 자식이 되도록 하는 특수한 splay 메서드
		while (x->p != g) {
			Node* p = x->p;
			if (p->p == g) {
				rotate(x);
				break;
			}
			Node* pp = p->p;
			if ((x == p->l) == (p == pp->l)) rotate(p), rotate(x);
			else rotate(x), rotate(x);
		}
		if (!g) root = x;
	}
	void get(int i) { // i번째 원소를 찾는 메서드
		Node* p = root;
		if (!p) return;
		p->propagate(); // 값을 찾아 내려가는 동안 propagate해줍니다.
		while (1) {
			while (p->l && p->l->size > i) p = p->l, p->propagate();
			if (p->l) i -= p->l->size;
			if (!i--) break;
			p = p->r;
			p->propagate();
		}
		splay(p);
	}
	Node* gather(int s, int e) {
		get(e + 1);
		Node* r = root;
		get(s - 1);
		Node* l = root;
		splay(r, l);
		l->r->l->update();
		return l->r->l;
	}
public:
	SplayTree() : root(0) {}
	~SplayTree() { if (root) delete root; }
	void init(int n) {
		if (root) delete root;
		root = new Node; // dummy
		Node* cur = root;
		ll x;
		for (int i = 0; i < n; ++i) {
			std::cin >> x;
			Node* next = new Node;
			next->val = next->sum = x;
			cur->r = next; next->p = cur;
			cur = next;
		}
		Node* tail = new Node; // dummy
		cur->r = tail; tail->p = cur;
		splay(tail);
	}
	void insert(int c, ll x) {
		get(c);
		Node* r = root;
		Node* l = root->l;
		Node* m = new Node;
		m->sum = m->val = x;
		m->l = l; l->p = m;
		m->p = r; r->l = m;
		m->update();
		r->update();
	}
	ll get_sum(int s, int e) { return gather(s, e)->sum; }
	void push(int s, int e, ll x, ll a0, ll d) { gather(s, e)->push(x, a0, d); }
} sp;
int N, Q;

int main() {
	std::cin.tie(0)->sync_with_stdio(0);
	std::cin >> N >> Q;
	sp.init(N);

	for (int i = 0, q, a, b, c, x; i < Q; ++i) {
		std::cin >> q;
		if (q == 1) { // 1번 쿼리
			std::cin >> a >> b >> x;
			sp.push(a, b, 0, x, 0); // 계수 0, 초항 x, 공차 0 쿼리를 push합니다.
		}
		if (q == 2) { // 2번 쿼리
			std::cin >> a >> b >> x;
			sp.push(a, b, -1, 0, x); // 계수 1, 초항 0, 공차 x 쿼리를 push합니다.
		}
		if (q == 3) {
			std::cin >> c >> x;
			sp.insert(c, x);
		}
		if (q == 4) {
			std::cin >> a >> b;
			std::cout << sp.get_sum(a, b) << '\n';
		}
	}
}

Categories

스플레이 트리의 삽입

스플레이 트리의 구간 쿼리와 Lazy propagation