백준 1250 - 색칠된 공들
정답률 1%에 도전한다! 이번에 건드려본 문제는 색칠된 공들입니다. 아무래도 역량평가 B형을 준비하면서 가장 중요한 역량은 문제 제한에 맞춘 자료구조를 통한 극한의 메모리 활용과, 그러면서도 빠르고 충실하게 작동하는 코드를 작성해내는 것이 아닐까 싶어서 골라봤습니다.
문제 자체는 단순합니다. \(N\)개의 연속된 공들 사이에서 같은 색인 공들을 찾습니다. 그 덩어리가 가장 큰 순서대로, 크기가 같다면 앞에 있는 순서대로 빼냅니다. 이를 반복하면서, \(K\)번째 공이 언제 빠지는지 찾으면 됩니다. (연속된 공들은 편의상 덩어리로 부르겠습니다.)
공을 빼내는 절차와 tie-break rule이 명확하니 사실 여기까지만 읽어보면 이게 왜 정답률이 1%인가 싶습니다. 우선순위대로 덩어리를 찾고, 제거하고, 합치는 과정들은 그리 어렵지 않게 떠올릴 수 있으니까요. 하지만 막상 문제의 민낯을 보게 되면 생각은 달라집니다. \(N\)이 무려 \(10,000,000\)입니다. 메모리 제한은 128MB이고요. int형이 4바이트니까, 어림잡아 3천만 칸의 int배열을 할당하면 그 크기는 120MB에 육박합니다. 제한 시간 내에 해결하기 위해 우선순위 큐도 하나 만들어야 함을 고려한다면, 문제의 공들을 나타내는 배열은 고작 숫자 2개로 만들어 내야만 한다는 얘기가 되죠.
문제는 거기서 그치지 않습니다. 연속된 공들이 얼마나 큰지, 어디서부터 어디까지인지, 색깔은 뭔지 찾는 모든 과정이 \(O(1)\) 안에 수행되어야 합니다. 이쯤되면 문제의 정답률이 박살난 것도 이해가 갑니다. 이 문제를 해결하는 방법이야 여러가지 있겠지만, 지금부터는 제가 접근한 방향을 설명드리고자 합니다.
차근차근 생각해봅시다. 덩어리가 가져야 하는 정보는 왼쪽 끝 점, 오른쪽 끝 점, 색깔 그리고 덩어리의 크기입니다.
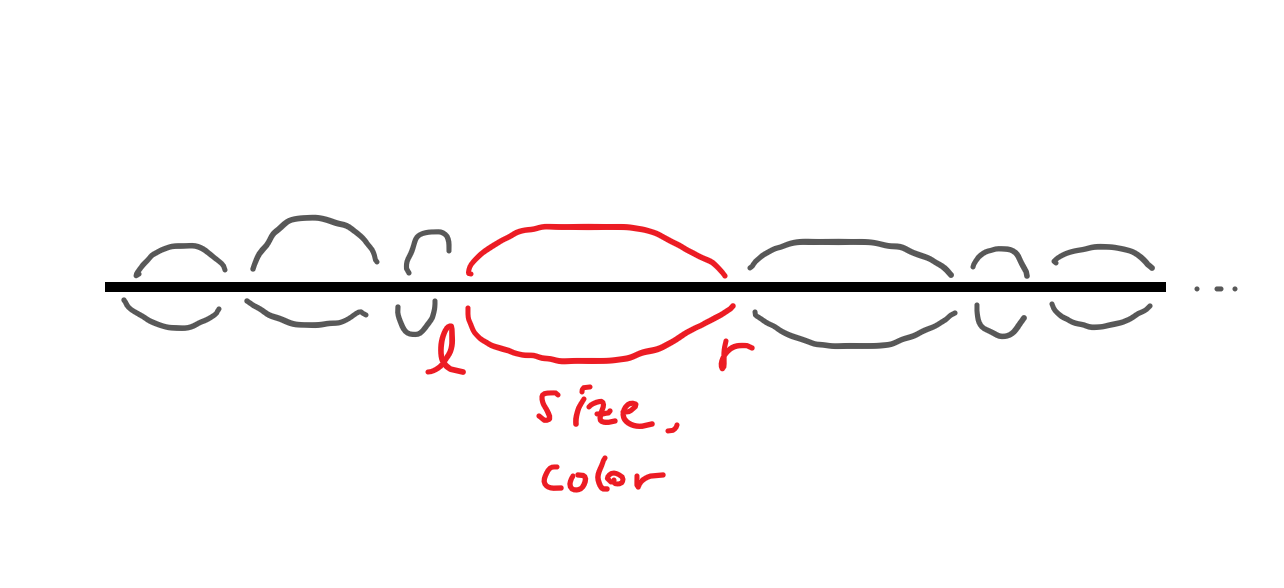
필요한 정보는 4개이므로, 하나의 덩어리마다 int 4개씩은 필요하지 않을까요. 하지만 잘 생각해보면 이는 3개로 줄일 수 있습니다. 색깔은 A부터 Z까지의 문자로 표현되므로, 필요한 비트 수는 그리 많지 않습니다. 다른 숫자들의 범위는 최대 천만이니까, 범위를 나타낼 숫자에 적당히 100 곱하고 색깔을 나타내는 문자를 더해버리겠습니다. 그럼 3개의 int형만 갖고도 왼쪽 끝, 오른쪽 끝, 크기를 모두 나타낼 수 있습니다.
여기서 뭘 더 줄일 수 있을까요? 남은 3개의 숫자는 모두 범위가 최대 천만이므로 다른 숫자 밑으로 넣거나 할 수는 없습니다. 어떤 두 숫자로부터 다른 한 숫자가 나온다면, 그 두 개만 갖고 있어도 될 것 같습니다. 예를 들자면, 오른쪽 끝에서 왼쪽 끝 좌표를 빼주면 크기가 나오는 것처럼요. 하지만 그리 단순하지 않습니다. 문제에서 수행되는 일은 결국 배열 중간에 있는 원소의 제거입니다. 가운데가 비어있을 수 있을 때, 좌표의 차는 항상 크기를 나타내지는 않습니다.
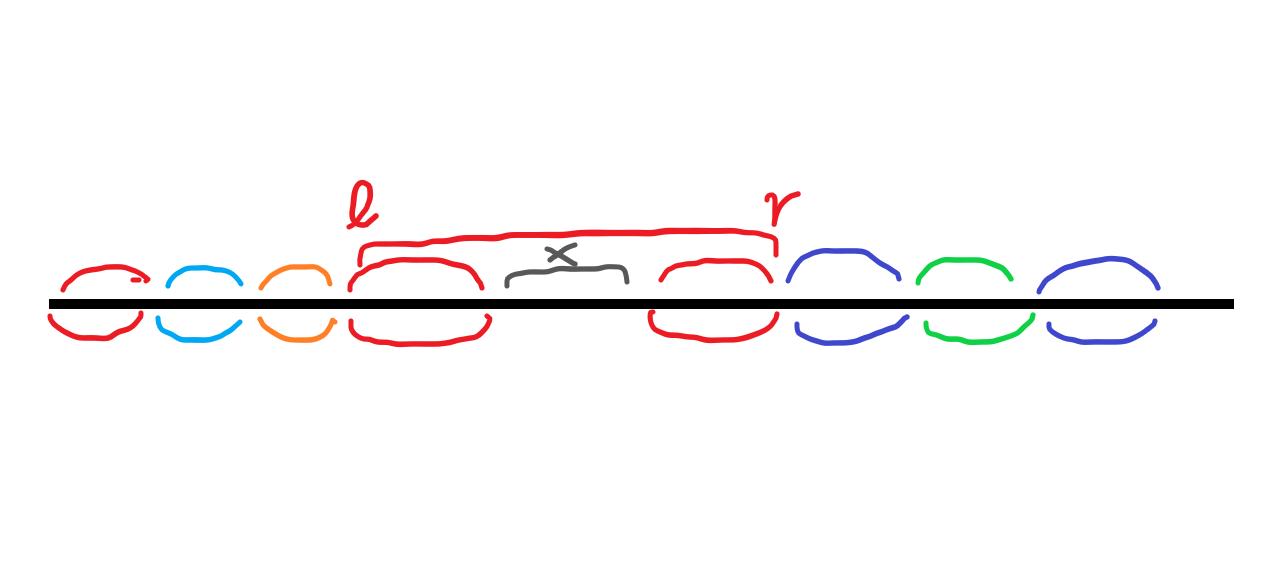
그럼 덩어리가 하나 제거될 때마다 배열 원소들을 앞으로 당겨서 빈 공간을 없애면 되지 않을까 싶지만, 이 작업에 소요되는 시간은 최악일 때 배열의 길이와 같다는 걸 생각해야 합니다. 덩어리의 크기는 결국 갖고 있어야만 하는 정보가 됩니다. 그럼 덩어리의 왼쪽과 오른쪽 좌표 중 하나를 날려야만 합니다. 그런데 잘 생각해보면, 덩어리를 나타낼 수 있는 int형의 개수는 3개 이상입니다.
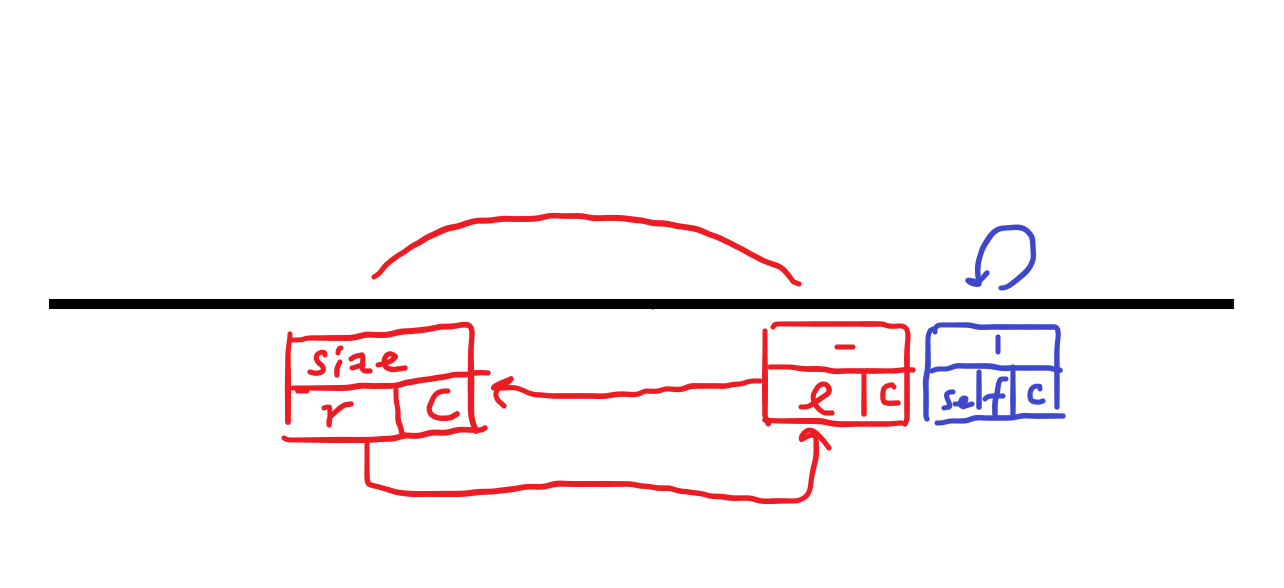
만약 좌우로 연속된 공이 없다면, 좌표는 자기자신을 가리키게 합니다. 덩어리의 크기가 2 이상이라면, 왼쪽 끝의 좌표는 오른쪽 끝을 가리키게 하고, 오른쪽 끝은 왼쪽 끝을 가리키게 할 수 있습니다. 마치 연결 리스트를 만들듯 하나의 노드를 만들어 줍니다. 물리적으로는 배열이지만, 논리적으로는 덩어리의 양쪽 끝에만 액세스 가능한 연결 리스트 자료구조를 만들었습니다.
기본적인 작업은 끝났으니, 실제 알고리즘 적용으로 들어갑시다. 연결 리스트에서 필요한 연산은 검색, 제거, 병합 세 가지입니다. 논리적 연결리스트를 만들어놓은 탓에 이 세 연산은 서로 유기적으로 맞물려 돌아가게 됩니다. 또한 우선순위의 덩어리를 빠르게 찾기 위해 이진 힙을 써야 합니다. 이진 힙에는 덩어리의 좌표와 크기 두 개의 정보를 모두 넣으면 좋겠지만, 그럴 여유는 없습니다. 좌표값만 대표로 넣고, 크기는 좌표로 위치를 찾아가서 참조하는 방식으로 만들어야 합니다.
병합
우선 최우선순위의 덩어리를 제거했다고 하겠습니다. 좌우의 색깔이 같아 합쳐야 할 때, 주의할 점은 다음과 같습니다.
-
준수한 실행 시간을 보장할 것
-
힙 상태를 무너뜨리지 않을 것
단순하게 생각하자면, 좌우 두 개의 노드를 하나로 만드는 거니까, 왼쪽 끝과 오른쪽 끝만 조작하면 될 것 같습니다.
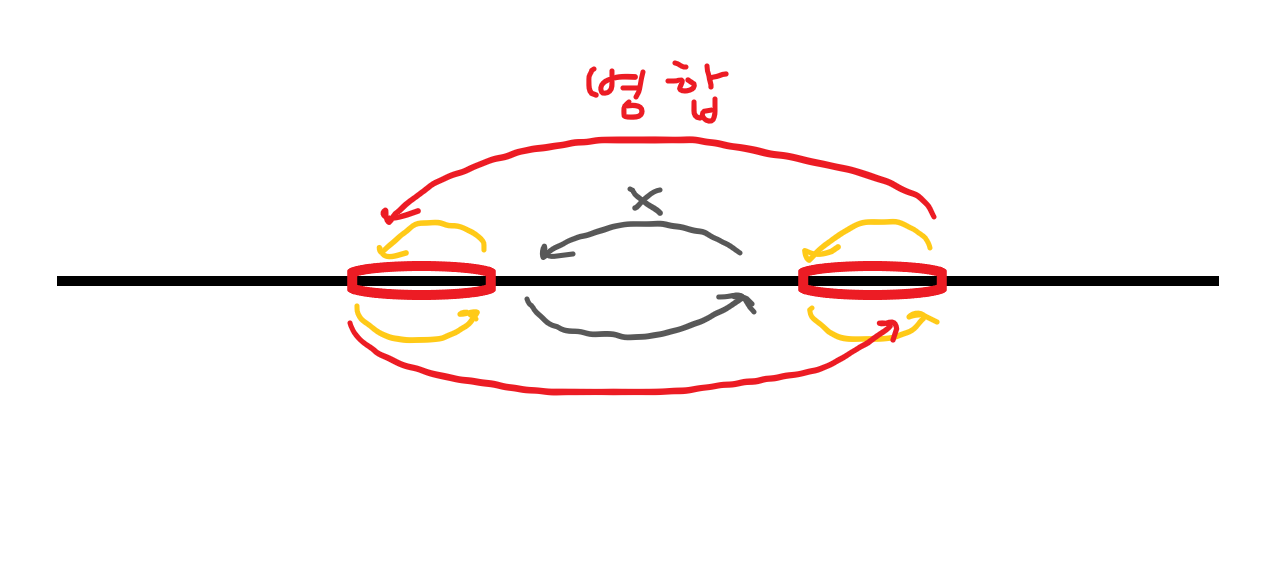
하지만 크기를 갱신하면서 힙 상태가 무너질 수 있습니다.
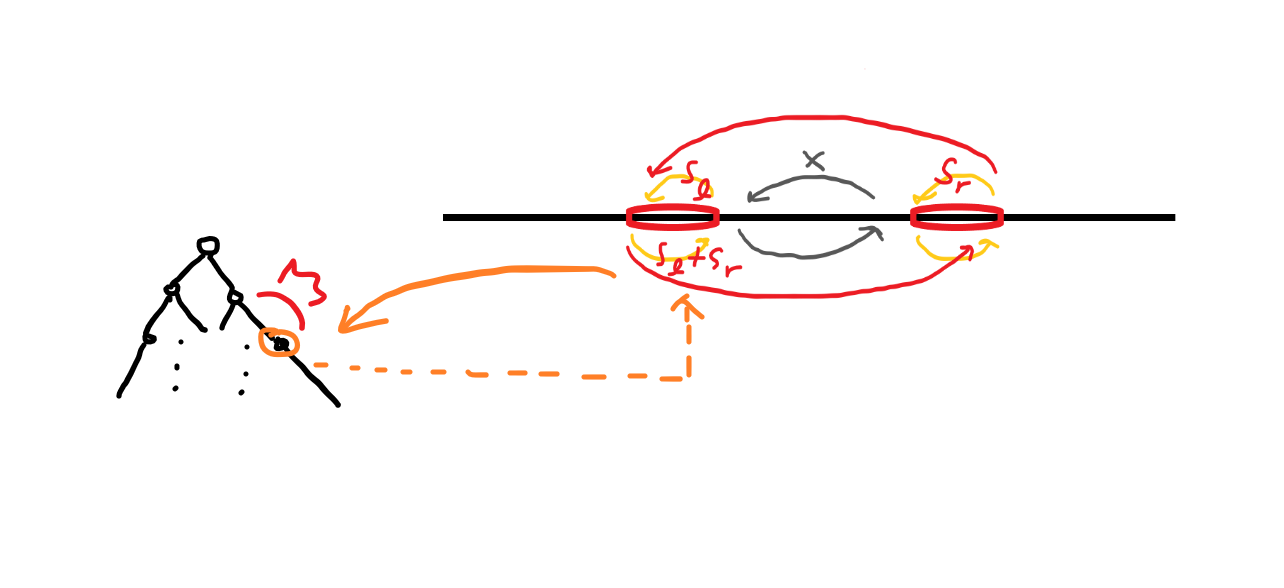
힙에 리터럴로 크기를 복사해 넣을 수 있으면 좋겠지만, 이 문제는 그렇게 충분한 메모리를 주지 않습니다. 왼쪽 끝의 크기를 함부로 바꿀 수는 없으니, 다른 방법을 찾아야 합니다. 다행히도, 방금 제거된 덩어리의 좌표는 더이상 힙 안에 없음을 보장할 수 있습니다. 그럼 병합 과정은 다음과 같이 이루어집니다.
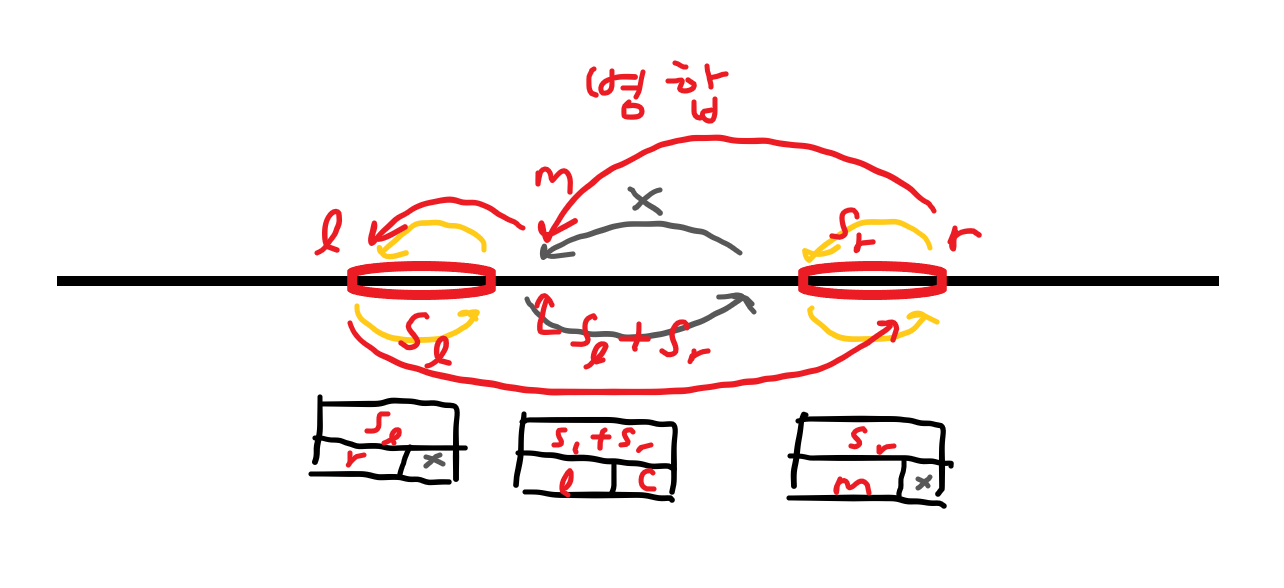
세 개의 노드를 사이클로 연결합니다. 방금 제거된 가운데 좌표 m에 합쳐진 덩어리의 색깔과 크기를 넣어줍니다. 좌우의 덩어리는 크기는 그대로 두고, 색깔을 없애서 병합되었음을 나타내줍니다.
이러한 병합 방식은 다소 복잡하고, 그렇게 아름다워보이진 않습니다. 다른 우아한 해결방법을 안다면 저에게 알려주세요.
검색
우선순위 큐에서 최우선순위인 덩어리의 좌표를 꺼냈다면, 덩어리의 정보는 쉽게 찾을 수 있습니다. 좌우의 덩어리 정보를 찾는 작업은 조금 복잡하지만, 오래 걸리지는 않습니다. (왼쪽 좌표) - 1 하면 왼쪽 덩어리의 오른쪽 끝을 찾습니다. 반대로 (오른쪽 좌표) + 1 하면 오른쪽 덩어리의 왼쪽 끝을 찾습니다. 추가적인 작업까지 기껏해야 너댓 번의 연산이면 좌우 덩어리의 정보는 모두 찾을 수 있습니다.
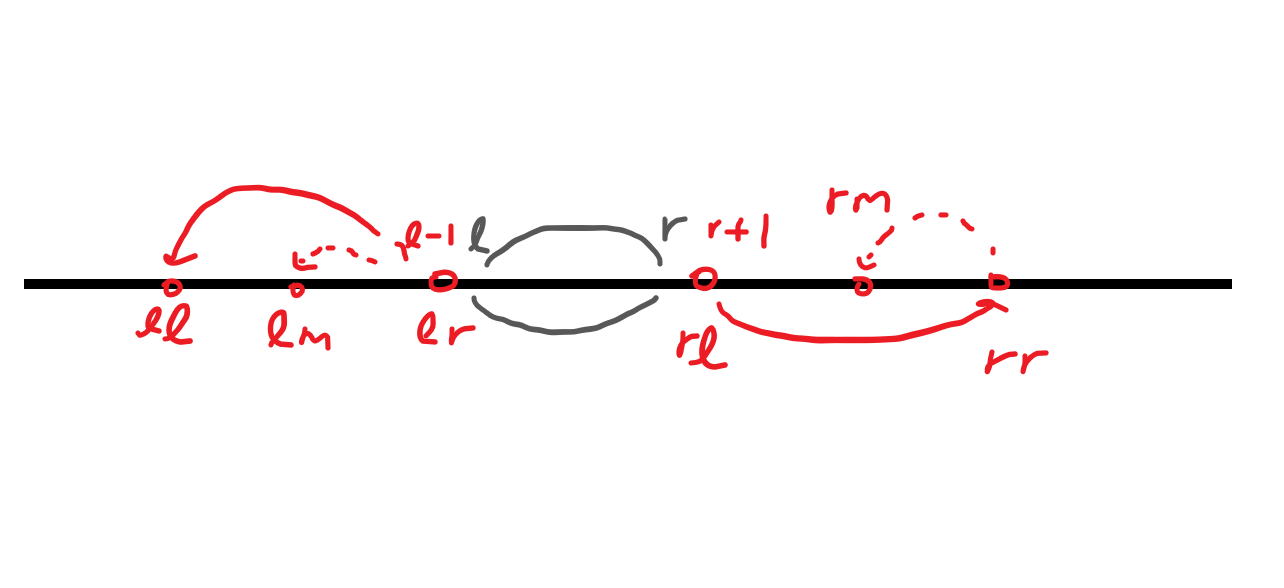
제거
덩어리를 제거하고나면, 좌우 병합을 해야하는지, 또는 할 수 없는지 판단합니다. 만약 병합해야 한다면, 위에서 설명한 병합 작업을 한 후, 좌표 m을 우선순위 큐에 넣습니다. 제거되어야 한다면, 연결리스트의 성질을 유지하기 위해 왼쪽 덩어리와 합쳐주겠습니다.
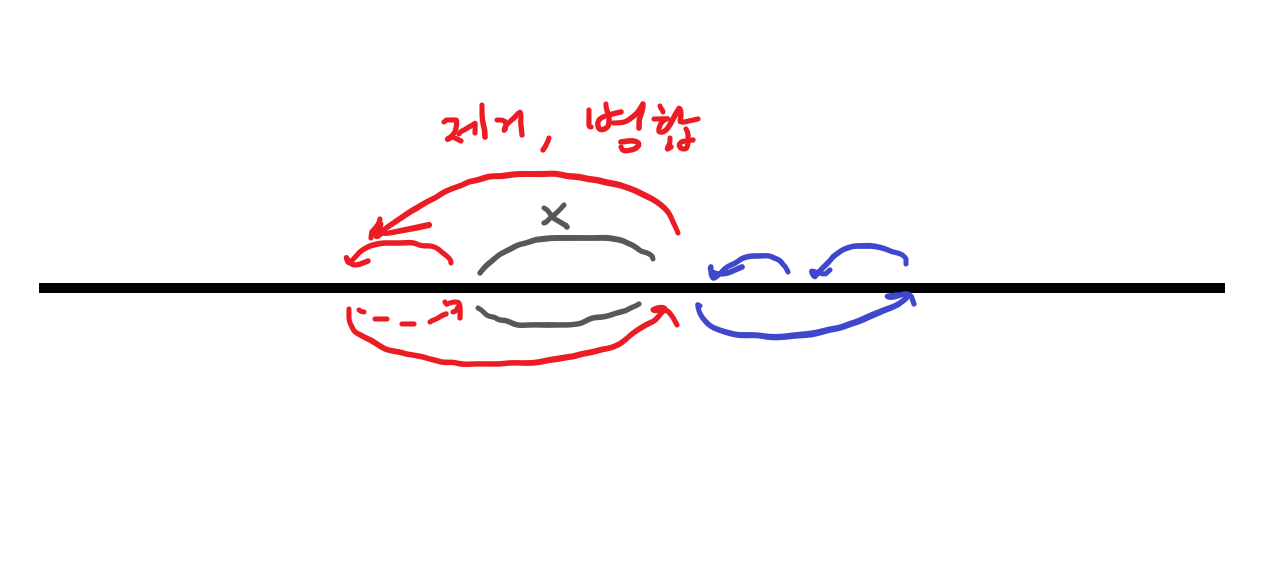
덩어리 제거 후 빈 공간만큼 원소를 당기거나 밀지 않고 좌우가 인접한 것처럼 논리적으로 만들어줍니다.
위의 모든 연산들은 \(O(1)\)로 수행됩니다.
밑은 예제 코드입니다.
#include <cstdio>
const int LEN = 10'000'001;
int N, K, i;
int _h, h[LEN]; // 이진 힙.
int p[LEN], s[LEN]; // p: (pos * 100 + c), s: size. 두 개의 배열이지만 저장되는 숫자는 3개입니다.
char c;
bool comp(int x, int y) { return s[x] > s[y] || s[x] == s[y] && x < y; }
// STL로는 메모리 제한 내에 해결할 수 없을 것 같아서 그냥 가벼운 힙을 직접 만들었습니다.
void push(int x) {
int j, y;
h[++_h] = x;
j = _h;
while (j > 1 && comp(x, y = h[j >> 1])) {
h[j] = y; h[j >> 1] = x;
j >>= 1;
}
}
int pop() {
int j, l, r, m, top = h[1];
h[1] = h[_h--];
j = 1;
while (j < _h) {
m = j;
l = j << 1;
r = j << 1 | 1;
if (l <= _h && comp(h[l], h[j])) m = l;
if (r <= _h && comp(h[r], h[m])) m = r;
if (m ^ j) {
l = h[m]; h[m] = h[j];
h[j] = l; j = m;
}
else break;
}
return top;
}
int main() {
scanf("%d%d", &N, &K);
scanf(" %c", &c);
p[1] = 100 + c;
s[1] = 1;
for (i = 2; i <= N; ++i) {
c = getchar();
if (p[i - 1] % 100 == c) { // 색이 같다면 덩어리로 연결해나갑니다.
p[i] = p[i - 1]; // 오른쪽 끝이 왼쪽 끝을 가리키게 합니다.
p[p[i] / 100] = i * 100 + c; // 왼쪽 끝이 오른쪽 끝을 가리키게 합니다.
++s[p[i] / 100]; // 크기 1 증가
}
else { // 색이 다르다면
push(p[i - 1] / 100); // 완성된 덩어리의 대표 좌표(왼쪽 끝)를 힙에 넣습니다.
p[i] = i * 100 + c;
s[i] = 1;
}
}
push(p[N] / 100);
for (i = 0; _h;) { // 힙에 원소가 존재할 동안
int cur, ptr, l, r, ll, lm = -1, lr, rl, rm = -1, rr, cl = 0, cr, fl = 1, fr = 1, sl, sr;
cur = pop();
ptr = p[cur] / 100;
c = p[cur] % 100; // 덩어리 좌표의 문자를 확인합니다. 0이라면 병합되었으므로 넘어갑니다.
if (!c) continue; // merged
++i; // 덩어리를 제거하고 횟수를 1 증가시킵니다.
l = ptr <= cur ? ptr : cur; // 왼쪽 끝 좌표를 확인합니다.
r = p[l] / 100; // 오른쪽 끝 좌표를 확인합니다.
if (l <= K && K <= r) break; // K번째 공이 제거되었다면 반복문을 빠져나갑니다.
lr = l - 1; // 왼쪽 덩어리의 오른쪽 끝 좌표는 (왼쪽 끝) - 1
ll = p[lr] / 100; // 왼쪽 덩어리의 왼쪽 끝 좌표를 확인합니다.
if (p[ll] / 100 < ll) { // 왼쪽 끝이 아니라면
lm = ll; // 병합된 가운데 좌표입니다.
cl = p[lm] % 100;
ll = p[lm] / 100;
sl = s[lm]; // 왼쪽 덩어리의 크기는 가운데 좌표가 갖고 있습니다.
}
else { // 왼쪽 끝이 맞다면
cl = p[ll] % 100;
sl = s[ll]; // 왼쪽 덩어리의 크기는 왼쪽 좌표가 갖고 있습니다.
}
if (!lr || !ll) fl = false; // 왼쪽 덩어리가 0번과 합쳐졌다면, 왼쪽에는 덩어리가 없다는 뜻입니다.
rl = r + 1; // 오른쪽 덩어리의 왼쪽 끝 좌표는 (오른쪽 끝) + 1
if (rl <= N) {
rr = p[rl] / 100; // 오른쪽 덩어리의 오른쪽 끝 좌표를 확인합니다.
if (p[rr] / 100 ^ rl) { // 오른쪽 끝의 포인터가 왼쪽 끝을 가리키지 않는다면
rm = p[rr] / 100; // 병합된 가운데 좌표입니다.
cr = p[rm] % 100;
sr = s[rm];
}
else {
cr = p[rl] % 100;
sr = s[rl];
}
}
else fr = false; // N 범위를 벗어난다면 덩어리는 없습니다.
// 왼쪽 끝과 오른쪽 끝에 덩어리가 있고 색이 같다면 합칩니다.
if (fl && fr && (cl == cr)) { // merge l + r, push l + r as cur
s[cur] = sl + sr;
(~lm ? p[lm] : p[ll]) = 0;
(~rm ? p[rm] : p[rl]) = 0;
p[cur] = ll * 100 + cl;
p[ll] = rr * 100;
p[rr] = cur * 100;
push(cur);
}
else { // merge l + cur
p[cur] = 0;
p[r] = (~lm ? lm : ll) * 100;
p[ll] = r * 100 + p[ll] % 100;
}
}
printf("%d", i);
return 0;
}
문제를 해결할 알고리즘을 만드는 게 어려운 문제는 아니었습니다. 단지 제한된 자원으로 문제를 해결할 자료 구조를 만들어내는 것이 관건인데, 이게 좀 어려워야죠.
그런데 이 문제, 막상 풀었는데도 맞힌 사람 목록에 올라가질 않습니다…?