백준 28227 - Dominoes

ICPC 문제인 Dominoes입니다.

동생이 추천받은 문제를 저에게 보여줬는데, 생각보다는 간단하게 풀릴 것 같아서 도전했습니다. 경제학이든 재무관리든, 그래프를 그리고 변형하는 연습을 해야 하는데, 그런 것에 익숙해지는 겸 풀었습니다.

임의의 서로 다른 위치에 놓인 도미노를 오른쪽에서 왼쪽으로 밀어 넘어뜨립니다. 그 때 넘어지는 도미노가 그리는 궤적의 총 합을 구하면 됩니다. 하나의 도미노가 넘어지면서 그리는 궤적은 사분원이고, 둘 이상의 사분원이 겹치는 넓이는 한 번만 계산됩니다. 단, 모든 \(i\)번째 도미노에 대한 면적을 구해야 합니다.

임의의 \(i\)번째 도미노를 넘어뜨렸을 때를 생각해봅시다. 그 때는 \(i-1\)번째 도미노의 궤적과 만나는 점을 찾고, 그 지점까지의 정적분 값을 구해줍니다. 그 다음엔 \(i-1\)번째 도미노가 그리는 궤적이 그 왼쪽 도미노와 만나는 점을 찾고,… 순서를 반대로 뒤집으면 귀납적으로 면적을 찾아줄 수 있습니다. 즉, \(S_{i-1}\)을 구하면 \(S_i\)를 빠르게 구할 수 있다는 뜻이 됩니다.

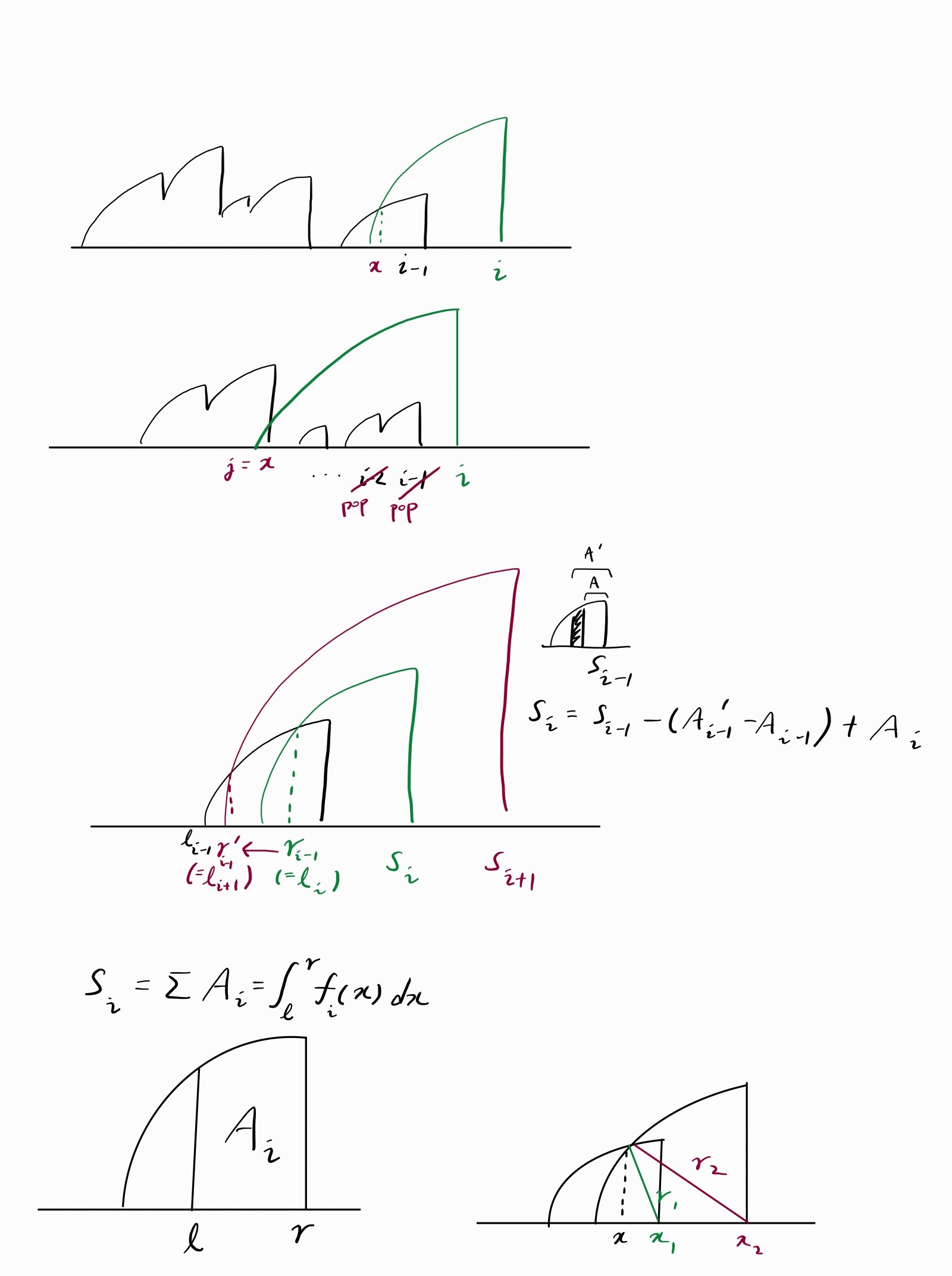
description

어떤 도미노 \(i\)를 넘어뜨려서 얻을 수 있는 궤적 \(S_i\)는 다음 과정을 통해 얻을 수 있습니다.

궤적에 완전히 포함되는 도미노는 제외해 나갑니다.
더이상 넘어뜨릴 수 있는 다음 도미노가 없다면 사분원만 그릴 수 있습니다.
처음으로 궤적의 일부만 걸치는 도미노 \(j\)를 찾았다면, 궤적의 일부만큼을 \(S_j\)에서 뺍니다. \(S_i\)의 넓이는 \(S_j+A_i\)가 됩니다.

위 3개 과정은 스택을 활용하여 구현할 수 있습니다. 한편 교점의 좌표 \(x\)는 식을 정리하면 얻을 수 있습니다. 피타고라스 정리에 의하여,

\[r_2^2 - (x_2 - x)^2 = r_1^2 - (x_1 - x)^2\] \[r_2^2 - r_1^2 = (x_2 - x)^2 - (x_1 - x)^2\] \[r_2^2 - r_1^2 = x_2^2 - 2x_2x - x_1^2 + 2x_1x\] \[r_2^2 - r_1^2 - x_2^2 +x_1^2 = -2x_2x + 2x_1x\] \[x = \frac{r_2^2 - x_2^2 - r_1^2 +x_1^2}{-2x_2 + 2x_1}\]

해가 존재하지 않는 등 몇 가지 예외를 처리한 후 그대로 구현하면 됩니다.

#include <iostream>
#include <cmath>

typedef long long ll;
typedef long double ld;
const int LEN = 200'001;
const ld PI = 3.1415926535;

ld intersect(const ll& x1, const ll& r1, const ll& x2, const ll& r2) {
	return (r2 * r2 - x2 * x2 - r1 * r1 + x1 * x1) / (ld)(-2 * x2 + 2 * x1);
}

int N, X[LEN], R[LEN], st[LEN];
ld S[LEN], l[LEN], r[LEN];

ld f(ld c, ld x, ld r) {
	ld y = sqrt(r * r - (x - c) * (x - c));
	ld fan = r * r * acos(y / r) / 2;
	ld tri = (c - x) * y / 2;
	return fan + tri;
}

int main() {
	std::cin.tie(0)->sync_with_stdio(0);
	(std::cout << std::fixed).precision(9);
	std::cin >> N;
	for (int i = 0, sp = 0, j; i < N; ++i) {
		std::cin >> X[i] >> R[i];
		l[i] = X[i] - R[i]; r[i] = X[i];
		while (sp) {
			j = st[sp - 1];
			if (X[j] <= X[i] - R[i]) break;
			if (R[i] * R[i] - (X[i] - X[j]) * (X[i] - X[j]) <= R[j] * R[j]) {
				S[i] += S[j];
				l[i] = X[j];
				break;
			}
			if ((l[i] = intersect(X[j], R[j], X[i], R[i])) > l[j]) {
				S[i] += (S[j] -= f(X[j], l[i], R[j]) - f(X[j], r[j], R[j]));
				r[j] = l[i];
				break;
			}	
			--sp;
		}
		st[sp++] = i;
		S[i] += f(X[i], l[i], R[i]);
		std::cout << S[i] << '\n';
	}
}

참고로 이 풀이를 동생에게 설명해주니 이런 원리를 그린 정리로 설명할 수 있다는군요. 누적합도 일부 쓰인 것 같고… 뭐 그렇습니다.

Categories