백준 19004 - Rikka with lines

페트로자보츠크 문제인 Rikka with Lines입니다.

개인적으로 페트로자보츠크 문제들은 입력 제한도 괴랄하고 풀이도 변칙적인 편이어서 그다지 좋아하지는 않지만 경제학 공부를 핑계로 직선 방정식 연습이나 할 겸 풀었습니다.

\(N\)개의 직선이 2차원 직교 좌표계를 가로지르고 있습니다. 좌표축에 평행한 임의의 직사각형 영역 내에서 교차하는 직선의 순서쌍 개수를 구하면 됩니다.

각 직선은 \(y=ax+b\)로 나타낼 수 있습니다. 문제의 조건 상 직선은 수직 또는 수평이 아님을 알 수 있습니다. 한편, 직선의 개수 제한 때문에 \(O(N^2)\)으로 풀기는 어렵습니다. 이 문제를 풀기 위한 핵심 아이디어는 다음과 같습니다.

직사각형의 가로 및 세로 길이는 정답과 관계가 있는가?
엇갈리는 두 직선에 대한 관계식을 어떻게 정의할 것인가?

topo

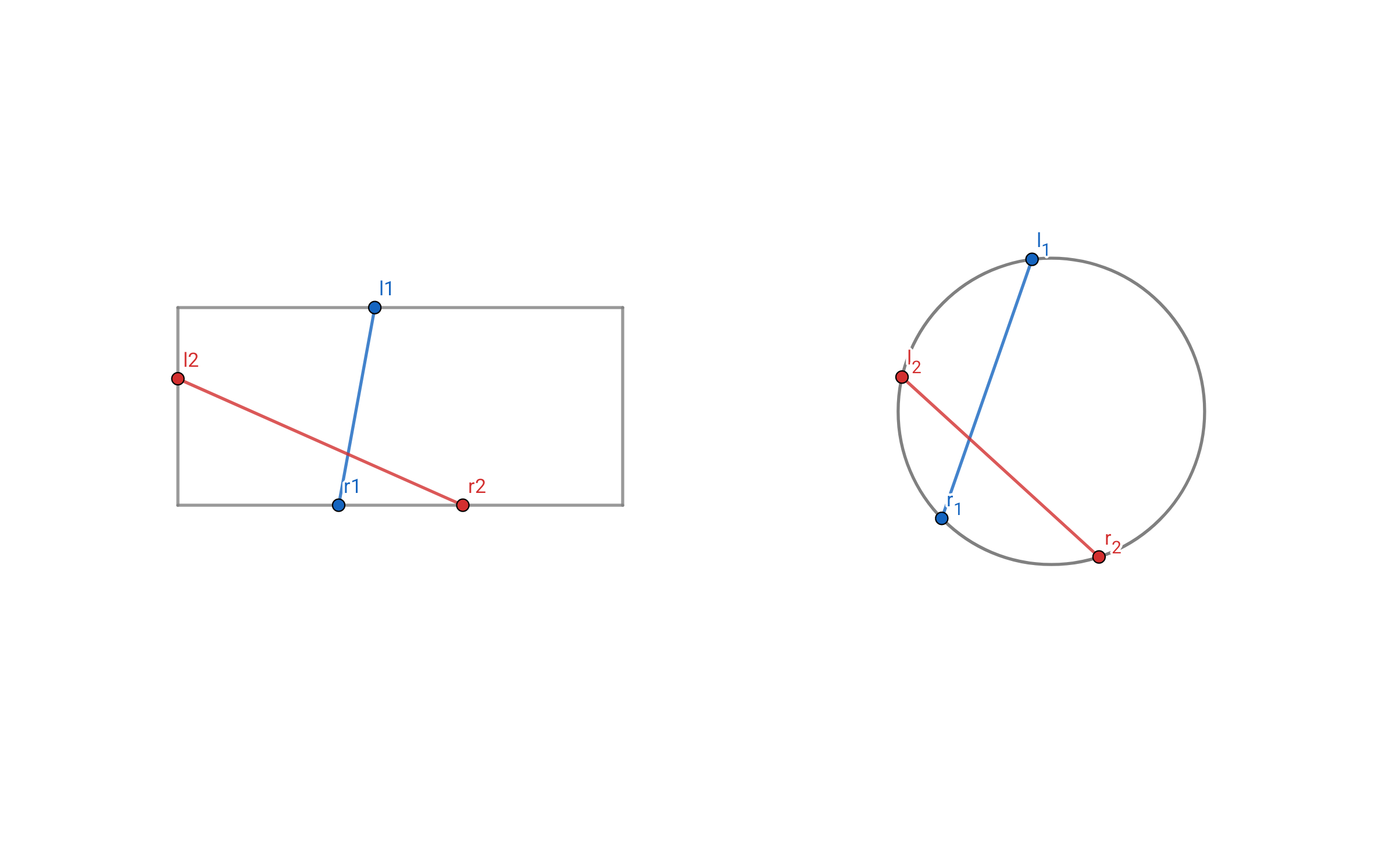
임의의 직사각형을 변형하여 원으로 만들었을 때, 교차하는 현의 여부는 변하지 않습니다. 물론 교차하는 점의 위치가 바뀔 수는 있지만, 엇갈리지 않던 선분이 엇갈리게 된다거나, 그 반대의 일은 일어나지 않습니다.

이제 엇갈리는 두 선분은 어떤 관계에 있는지가 핵심입니다. 원의 한 점을 1번으로 두고, 반시계 방향으로 번호를 붙여나간다고 합시다. 다음 식을 만족할 때 두 선분은 교차합니다.

\[l_1 \le l_2 \le r_1 \le r_2\]

어떤 선분과 교차하는 다른 선분들의 개수를 구하고자 한다면, 현으로 잘라낸 호 위에 \(l\) 점만 있거나 \(r\)점만 있는 것의 개수를 찾을 수 있도록 구간 쿼리를 처리해야 합니다. 이는 기초적인 플레인 스위핑과 펜윅트리로 구현할 수 있습니다.

use std::io::{self, BufRead, Write};
use std::cmp::Ordering;
use std::ops::Neg;

#[derive(Debug, Clone, Copy)]
struct Rational(i128, i128);

impl Rational {
    fn normalize(&self) -> Self;
}

fn gcd(a: i128, b: i128) -> i128;

impl Neg for Rational;

impl PartialEq for Rational;
impl Eq for Rational {}

impl PartialOrd for Rational;
impl Ord for Rational;

struct FenwickTree {
    tree: Vec<i64>,
    size: usize,
}

impl FenwickTree {
    pub fn new(size: usize) -> Self;
    pub fn sum(&self, idx: usize) -> i64;
    pub fn add(&mut self, idx: usize, value: i64);
}

fn main() {
    let mut iter = io::stdin().lock().lines();
    let mut writer = io::BufWriter::new(io::stdout());

    let t: usize = iter.next().unwrap().unwrap().trim().parse().unwrap();
    for _ in 0..t {
        let v: Vec<i128> = iter.next().unwrap().unwrap()
            .split_whitespace().map(|x| x.parse().unwrap()).collect();
        let (n, x1, y1, x2, y2) = (v[0] as usize, v[1], v[2], v[3], v[4]);

        let mut seg: Vec<(usize, usize)> = vec![(0, 0); n];
        let mut pos: Vec<(i32, Rational, usize, usize)> = vec![];
        for i in 0..n {
            let v: Vec<i128> = iter.next().unwrap().unwrap()
                .split_whitespace().map(|x| x.parse().unwrap()).collect();
            let (a, b) = (v[0], v[1]);
            let p1 = Rational(y2 - b, a).normalize();
            let mut dir = 0;
            if Rational(x1, 1) < p1 && p1 <= Rational(x2, 1) {
                pos.push((1, -p1, i, dir));
                dir += 1;
            }
            let p2 = Rational(a * x1 + b, 1);
            if y1 < p2.0 && p2.0 <= y2 {
                pos.push((2, -p2, i, dir));
                dir += 1;
            }
            let p3 = Rational(y1 - b, a).normalize();
            if Rational(x1, 1) <= p3 && p3 < Rational(x2, 1) {
                pos.push((3, p3, i, dir));
                dir += 1;
            }
            let p4 = Rational(a * x2 + b, 1);
            if y1 <= p4.0 && p4.0 < y2 {
                pos.push((4, p4, i, dir));
                // dir += 1;
            }
        }
        pos.sort();

        let mut idx = 1;
        seg[pos[0].2].0 = idx;
        seg[pos[0].2].1 = idx;
        for i in 1..pos.len() {
            if pos[i].0 != pos[i - 1].0 || pos[i].1 != pos[i- 1].1 { idx += 1; }
            seg[pos[i].2].1 = idx;
            if pos[i].3 == 0 {
                seg[pos[i].2].0 = idx;
            }
        }
        seg.sort();

        let mut f = FenwickTree::new(idx);
        let mut ret: i64 = 0;
        for (l, r) in seg {
            if l == 0 { continue; }
            ret += f.sum(r) - f.sum(l - 1);
            f.add(r, 1);
        }
        _ = writeln!(writer, "{}", ret);
    }

    writer.flush().unwrap();
}

Categories