대회 문제로 나온 점프입니다.

실제 대회 당시에는 아르바이트를 하고 있어서 제출하지 못했지만 머릿속으로 생각해둔대로 풀었습니다. 언뜻 보기에는 문제가 복잡해보이지만 실상은 지극히 단순한 사실 하나를 잡아내는 순간 \(O(N)\)으로 풀 수 있습니다.

어떤 위치 \(a\)에서 다른 위치 \(b\)로 이동할 수 있음은 다음을 의미합니다: \(a\)와 \(b\) 사이에 있는 점들은 반드시 \(a\) 또는 \(b\)를 지나야 바깥으로 나갈 수 있다.

또한, 이동 비용이 높이 차이에 의해서만 정의된다는 점에서, 다음 특성을 만족합니다: 가장 많은 정점을 거치는 경로가 최적 경로가 된다.

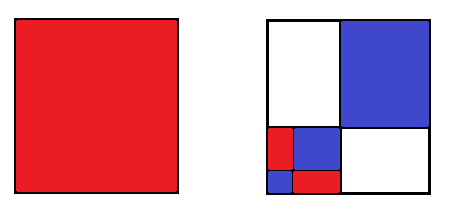
optimal_cost

높이 차의 제곱을 빨간색이라 할 때, 정점 하나를 거칠 때마다 그 비용은 반드시 더 적어지거나 같습니다.

한편, 어떤 정점에서 다른 정점으로 이동하기 위한 최소 비용 경로를 최적 경로라고 합시다. 그렇다면 최적 경로는 위에서 말했던 성질들에 의해 이진 트리를 구성합니다.

tree

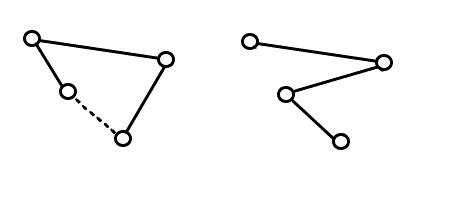
되도록 가장 많은 점을 거쳐야 한다는 것은, 어떤 점에서 다른 점으로 이동하기 위한 경로를 구하기 위해 여러 경우의 수를 고려할 필요가 없다는 뜻이 됩니다. 어떤 정점의 왼쪽 또는 오른쪽으로 높이가 낮은 정점으로의 이동 경로가 2개 이상 있다면 어떤 한 점으로의 이동 경로는 반드시 줄일 수 있습니다. 즉, 좌우로는 2개의 경로만 존재할 수 있습니다.

트리를 만드는 과정은 스택을 활용하면 \(O(N)\)으로 수행 가능합니다. 트리를 만드는 동시에 답을 구할 수도 있습니다.

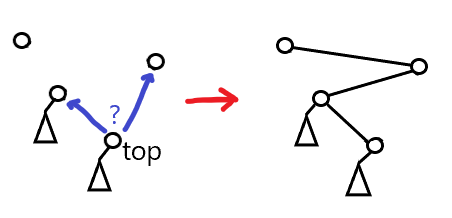
making_tree

스택에 높이 내림차순이 되도록 정점을 넣습니다. 위치 \(i\)의 높이 \(h_i\)에 대해, 다음 과정을 수행합니다.

  • \(h_{top}\)이 더 높다면 스택에 \(h_i\)를 스택에 넣고 종료한다.

  • \(h_{top}\)이 더 낮다면 스택에서 뺀다. 스택에서 뺀 정점을 자식으로 하여 부모 노드 밑에 붙인다.

  • 부모 노드는 그 밑에 있던 정점 \(h_{top}’\)과 \(h_i\) 중 높이가 낮은 쪽으로 한다.

위의 간단한 과정으로 최적 경로 트리를 만들 수 있습니다. 정답을 구하는 방법도 간단합니다.

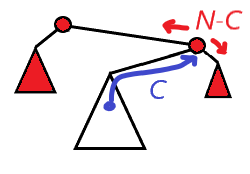
count

어떤 서브트리와 부모를 연결하는 간선을 지나는 경로의 수는 항상 정해져 있습니다. 서브트리에서 위로 올라와야만 하는 정점의 수는 서브트리의 크기가 됩니다. 그리고 각 정점은 서브트리를 제외한 다른 정점들로 한 번씩 가야 하므로 전체 트리 크기 - 서브트리 크기만큼 지나야 합니다.

남은 것은 별로 복잡하지 않은 구현입니다.

#include <iostream>

typedef long long ll;
const int LEN = 500'001;
const ll MOD = 1e9 + 7;
int N, h[LEN], C[LEN], sp, S[LEN];

int main() {
	std::cin.tie(0)->sync_with_stdio(0);
	std::cin >> N;

	ll ret = 0;
	for (int i = 0, j, k; i < N; ++i) {
		std::cin >> h[i];
		C[i] = 1;
		while (sp && h[S[sp - 1]] <= h[i]) {
			j = S[--sp];
			k = sp && h[S[sp - 1]] < h[i] ? S[sp - 1] : i;
			ret = (ret + ((ll)N - C[j]) * C[j] % MOD * (h[k] - h[j]) % MOD * (h[k] - h[j])) % MOD;
			C[k] += C[j];
		}
		S[sp++] = i;
	}
	std::cout << ret;
}