백준 22872 - 공 옮기기

그런대로 풀 수는 있지만 만점 받기는 참 힘든… 공 옮기기입니다. 문제도 짧고 정해 코드도 100줄 안으로 짤 수 있지만 풀이를 찾기까지의 과정이 지극히 어려운 문제입니다. 어쩌다 이 문제를 발견한 건지는 저도 모릅니다. 그냥 문제가 짧고 쉬워보여서 점찍어둔 것 같은데, 난이도를 까보고 반쯤 포기했다가 다시 풀었습니다. 25점까지 받고 정해 코드를 이리저리 찾아봤습니다. 만점을 받은 후엔 다른 사람들의 코드를 참고해서 예쁘게 다듬었습니다. 참고 바랍니다.

BFS (10점)

일단 아무런 규칙도 찾지 않은 상태에서 접근해봅시다.

1번 상자와 2번 상자에 담긴 공을 비트마스킹하여 상태 관리를 할 수 있고, 각 상태에서 다음 상태로 갈 수 있는 경우는 최대 6개 존재할 수 있습니다. \(1..N, 0, 0\) 에서 \(0, 0, 1..N\)으로 가는 최단 경로를 찾는 문제로 생각할 수 있고 BFS를 수행하여 풀 수 있습니다. 이 경우, 상태의 개수가 병목인데 \(N\)개의 공이 독립적으로 각 상자에 담길 수 있으므로 \(3^N\)개의 상태(!)가 있고… 시간 초과를 받게 됩니다.

std::map<int, int> visited[1 << 20];
int N;
int cnt = 0;

int get_middle(int s);
struct State { int s1, s2, s3; };
int bfs(int n) {
	std::queue<State> q;
	q.push({ (1 << N) - 1, 0, 0 });
	visited[(1 << N - 1)][0] = 0;
	cnt++;

	while (q.size()) {
		State s = q.front(); q.pop();

		if (s.s1 == 0 && s.s2 == 0) return visited[0][0];

		int s1 = s.s1, s2 = s.s2, s3 = s.s3;
		int d = visited[s1][s2];

		if (s1) {
			int m1 = get_middle(s1);
			int ss1 = s1 & ~(1 << m1);
			if (get_middle(s2 | 1 << m1) == m1) {
				int ss2 = s2 | 1 << m1;
				if (visited[ss1].find(ss2) == visited[ss1].end()) {
					visited[ss1][ss2] = d + 1;
					q.push({ ss1, ss2, s3 });
					cnt++;
				}
			}
			if (get_middle(s3 | 1 << m1) == m1) {
				int ss3 = s3 | 1 << m1;
				if (visited[ss1].find(s2) == visited[ss1].end()) {
					visited[ss1][s2] = d + 1;
					q.push({ ss1, s2, ss3 });
					cnt++;
				}
			}
		}
		if (s2) {
			int m2 = get_middle(s2);
			int ss2 = s2 & ~(1 << m2);
			if (get_middle(s1 | 1 << m2) == m2) {/**/}
			if (get_middle(s3 | 1 << m2) == m2) {/**/}
		}
		if (s3) {/**/}
	}
	return -1;
}

이 방법은 정해를 빠르게 찾기에 그닥 유효한 방법은 아니지만, \(N=15\)일 때까지의 답은 손에 넣을 수 있게 해줍니다. 시각화하는 등의 방법으로 규칙을 추론하는 데 도움이 될 수 있습니다. 물론 이런 고생 하지 않고도 규칙을 찾을 수 있겠지만… 저에겐 무리였습니다.

하노이의 탑 (25점)

\(N=7\)일 때까지의 답은 비교적 짧고 단순하여 패턴을 파악하기 쉬웠습니다. 가만히 보니 하노이의 탑이었습니다.

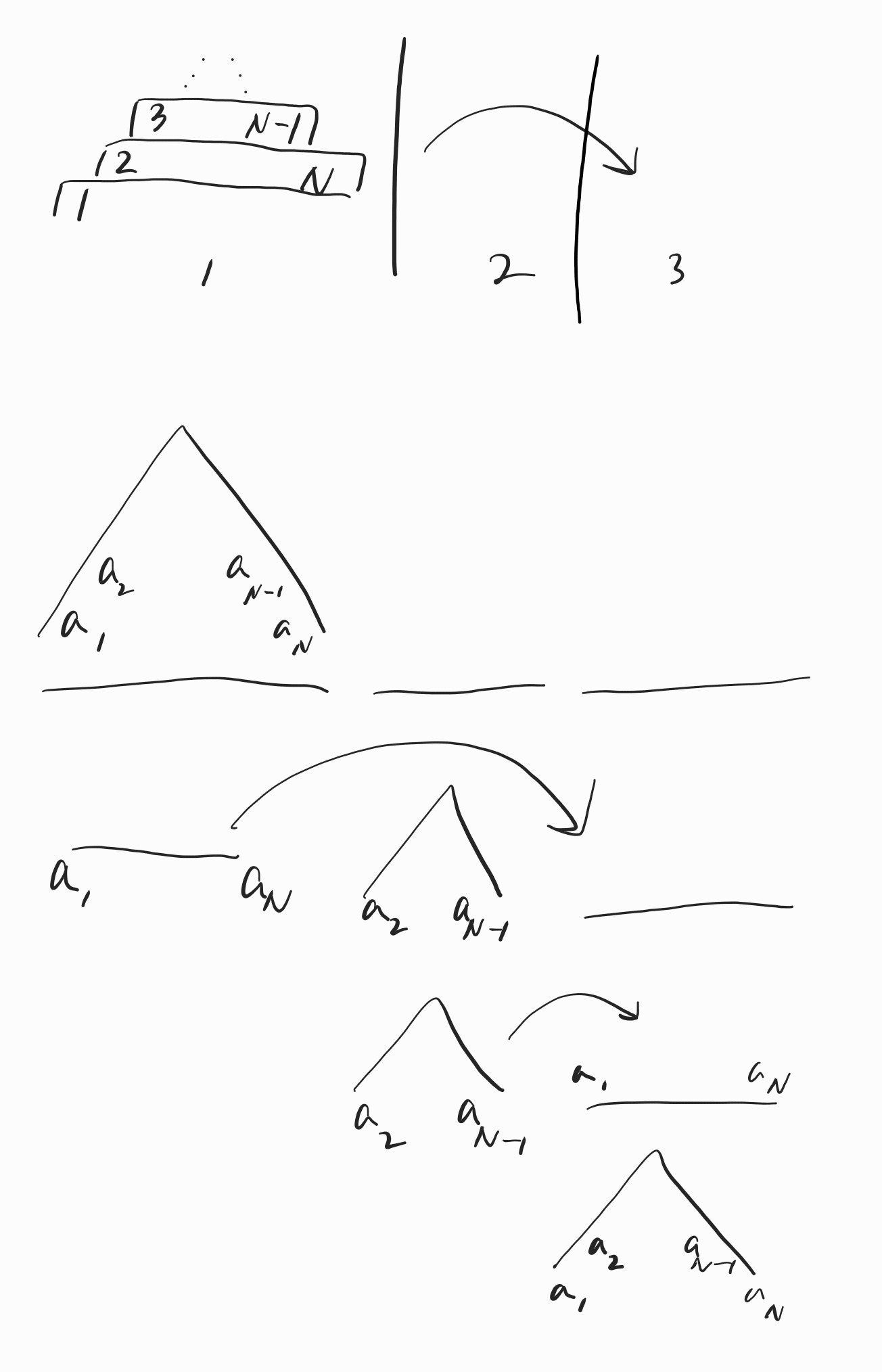
hanoi_1

탑의 각 원반이 양쪽으로 갈라져 있을 뿐, 기본적인 원리는 보통의 하노이의 탑과 다르지 않았습니다. 하지만 아주 약간 다른 점이 하나 있고, 이것이 25점 코드와 26점 코드를 가르는 원인이 됩니다.

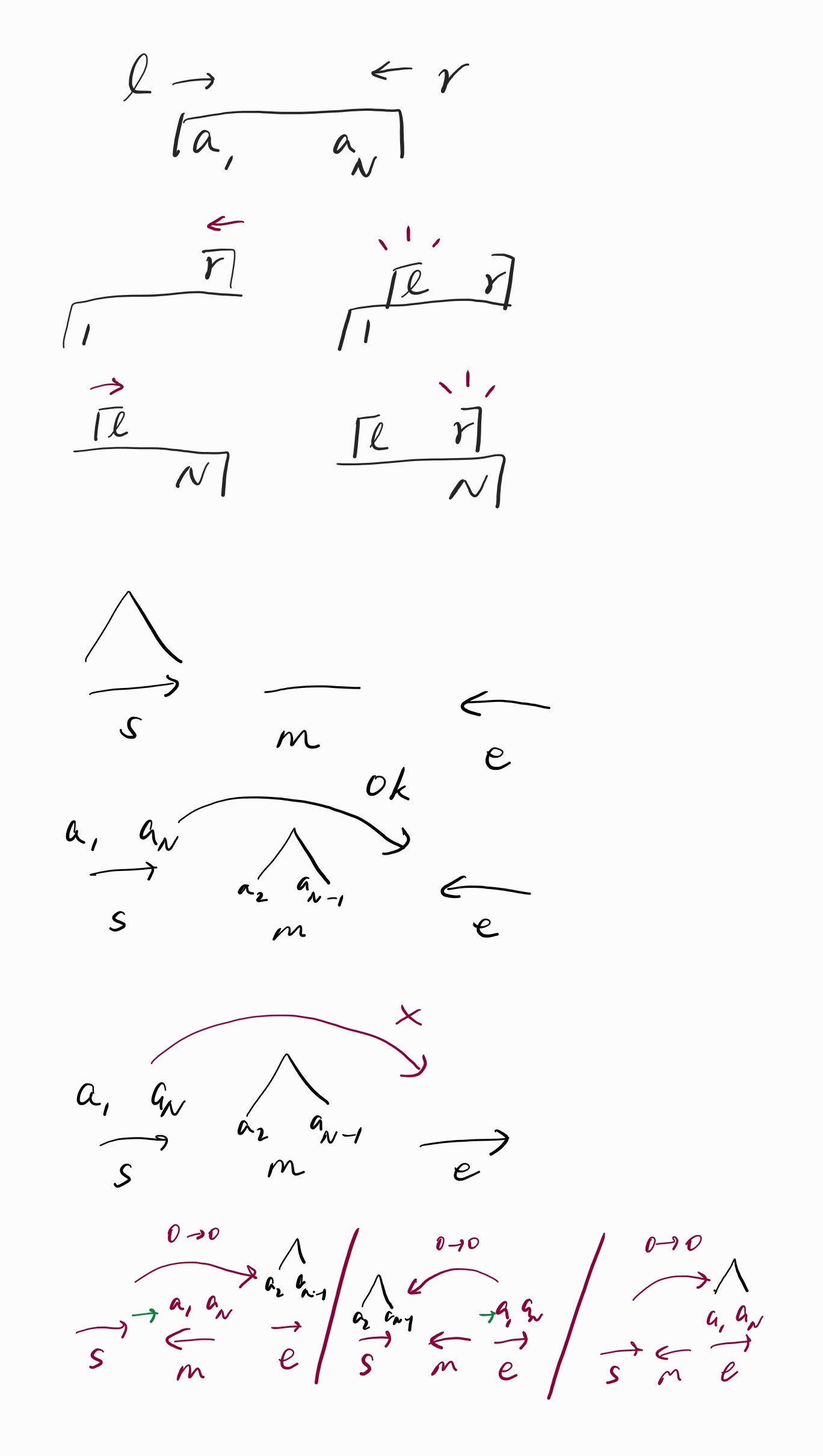
hanoi_2

원반의 양 조각은 왼쪽과 오른쪽으로 구분됩니다. 기둥 또한 마지막으로 올라간 조각의 방향에 따라 각 상태가 구분되어, 다음에는 반대 방향 조각만 올라갈 수 있습니다. 기둥 \(s\)에서 \(e\)로 옮길 때, 두 기둥의 상태가 다르다면 왼쪽과 오른쪽 조각이 서로 역순으로 들어가므로 보통의 하노이 탑처럼 옮기면 됩니다.

하지만 두 기둥의 상태가 같은 경우 \(s\)에서 \(e\)로 바로 옮길 수는 없고, 나머지 기둥인 \(m\)을 경유하여 두 번에 걸쳐 옮겨야 합니다.

#include <iostream>

const int LEN = 1'000'001;

int len, u[LEN], v[LEN];
inline void move(int s, int e) { u[len] = s; v[len] = e; len++; }

void hanoi(int n, int s, int m, int e, int state = -1) {
	if (!~state) {
		hanoi(n - 1, s, e, m, 1 << s);
		move(s, e);
		hanoi(n - 1, m, s, e, 1 << e);
		return;
	}
	if (n <= 0) return;
	if (n == 1) {
		move(s, e);
		return;
	}
	if (((state >> s) & 1) ^ ((state >> e) & 1)) { // 상태가 다를 때
		hanoi(n - 2, s, e, m, state);
		move(s, e); move(s, e);
		hanoi(n - 2, m, s, e, state);
	}
	else { // 상태가 같을 때
		if (n == 2) {
			move(s, m); move(s, e); move(m, e);
			return;
		}
		hanoi(n - 2, s, m, e, state);
		move(s, m); move(s, m);
		hanoi(n - 2, e, m, s, state);
		move(m, e); move(m, e);
		hanoi(n - 2, s, m, e, state);
	}
}

int main() {
	int N;
	std::cin >> N;
	hanoi(N, 1, 2, 3);
	std::cout << len << '\n';
	for (int i = 0; i < len; ++i) std::cout << u[i] << ' ' << v[i] << '\n';
}

이 정도만 되어도 쓸만한 부분 정해 코드입니다만, 한 가지 하자가 있습니다.

이동 횟수를 구하는 재귀식을 정리해보면 다음과 같습니다.

상태가 다른 기둥으로 옮길 때 \(F(n)=F(n-2)+F’(n-2)+2\)입니다.
상태가 같은 기둥으로 옮길 때 \(F’(n)=3F’(n-2)+4\)입니다.

거의 \(3^{N/2}\)에 비례하게 되는데, 실제로 \(N=26\)일 때 150만 번을 넘어가게 됩니다. 횟수를 줄여야만 합니다.

하노이의 탑, 근데 이제 원반 쪼개기를 곁들인 (26점)

단순 하노이의 탑 재귀와 BFS로 찾은 최소횟수를 비교해보면 \(N=8\)일 때부터 차이가 납니다. (81, 73)

실제 그 과정을 살펴보면, 상태가 같은 기둥으로 옮길 때 원반의 한쪽 끝 조각이 일정한 규칙을 갖고 좌우로 번갈아 움직임을 관찰할 수 있습니다. 궁금하다면 실제 정해를 분석해보셔도 좋습니다. 8 9 15

그 방법을 정리하면 다음과 같습니다.

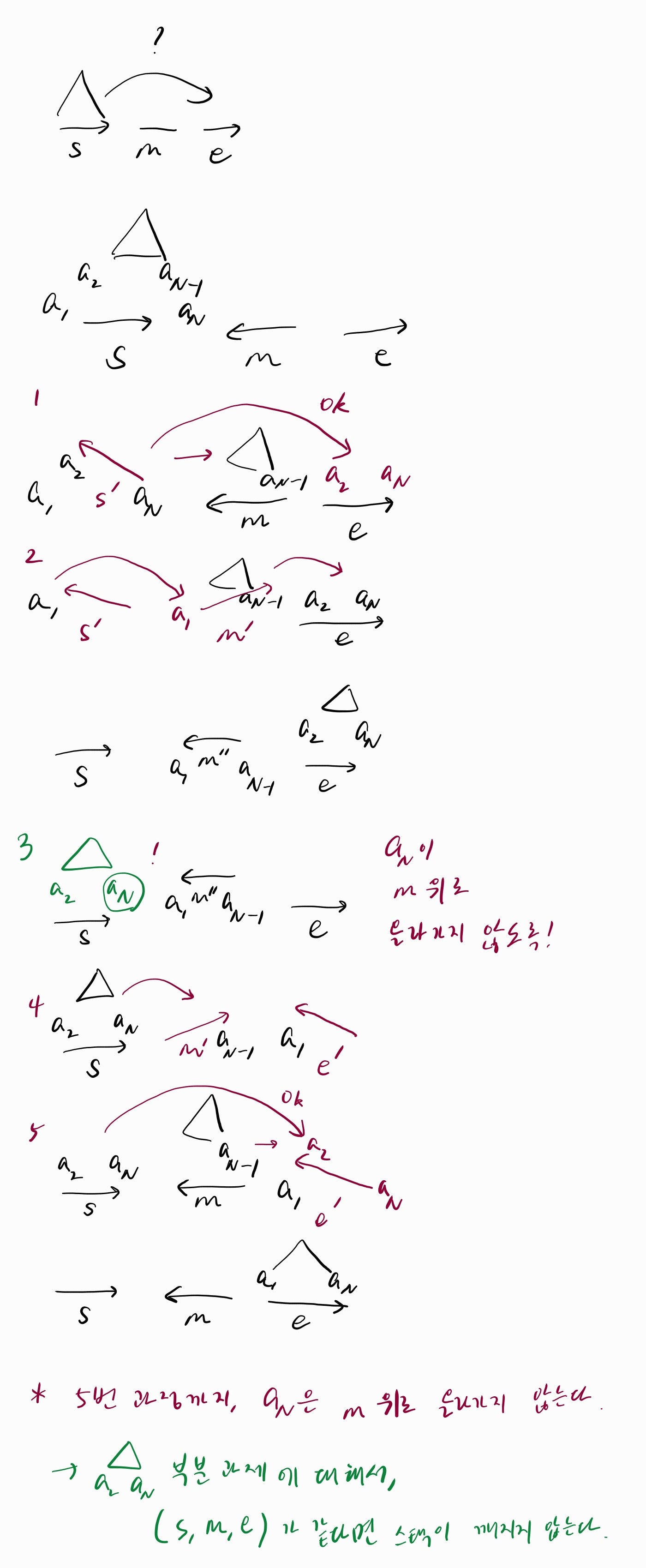
hanoi_3

\(N-3\)개의 조각을 \(m\)으로 옮깁니다. 이 때 기둥 \(s\)의 상태가 뒤집힙니다. \(a_2, a_N\)순으로 옮길 수 있습니다.
\(m\)에서 \(e\)로 \(N-4\)개의 조각을 옮깁니다. \(m\)의 상태가 뒤집힙니다. \(a_1\)을 \(m\)으로 옮깁니다.
\(a_2,..,a_N\) 조각을 \(e\)에서 \(s\)로 옮깁니다. 이 때 \(a_N\)이 절대 \(m\)에 올라가지 않도록 해야 합니다.
\(a_1\)을 \(m\)에서 \(e\)로 옮깁니다. \(e\)의 상태가 뒤집힙니다. \(N-4\)개의 조각을 \(s\)에서 \(m\)으로 옮깁니다.
\(s\)와 \(e\)의 상태가 다르므로 \(a_N, a_2\)순으로 옮길 수 있습니다. \(N-3\)개의 조각을 \(e\)로 옮겨 마무리합니다.

\(a_N\)의 위치를 보면, 3번 과정을 제외하고는 \(m\)에 위치하지 않습니다. 3번 과정이 이루어지는 동안 재귀적으로 \(m\)에 위치하지 않도록 해줄 수 있어야 합니다. 1, 2, 4, 5번 과정은 안전하므로, 3번 과정의 마지막에 처리되는 base case를 잘 정의하는 것이 중요합니다.

상태가 다른 경우를 처리하는 함수 \(F’(n)\)은 \(N \ge 4\)부터 호출됩니다. 고려해야 하는 base case는 4가지입니다.

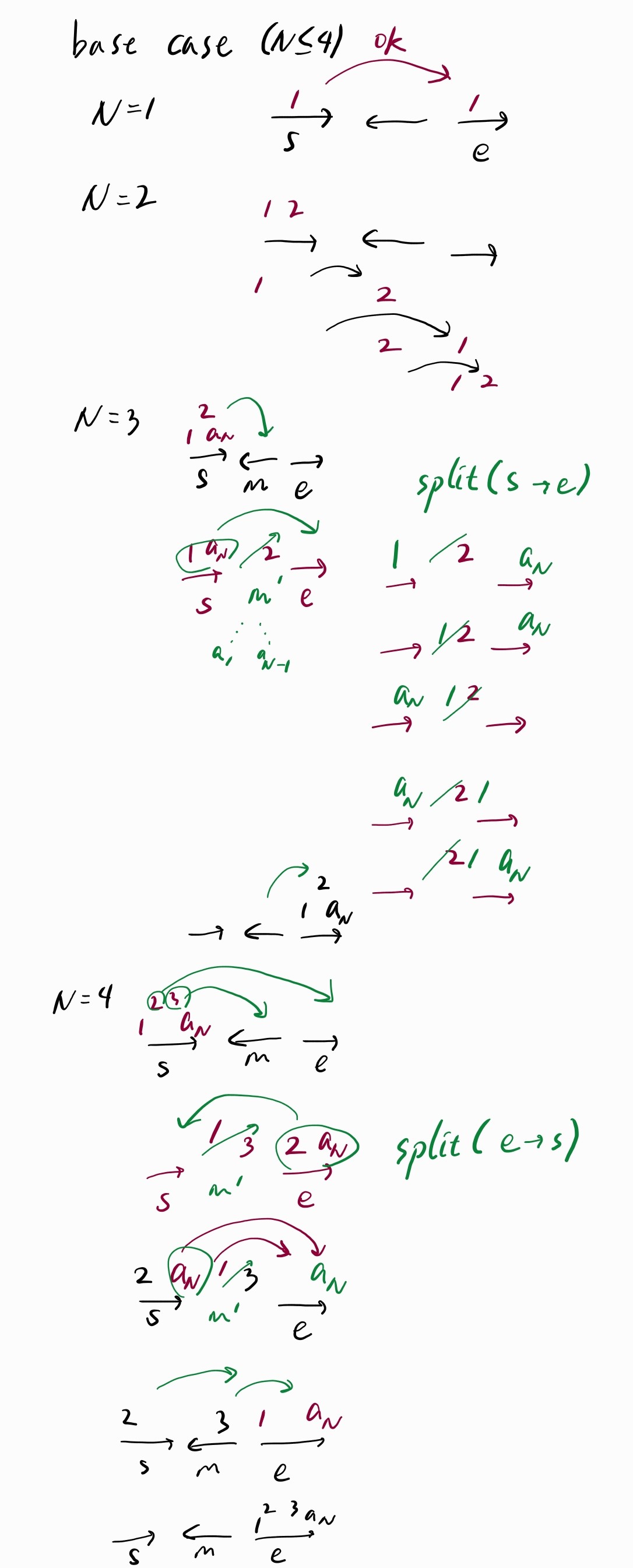
hanoi_4

\(F’(n-4)\)를 호출하는 위치에서는 \(a_N\)을 조작하지 않기 때문에, \(F’(n-2)\)는 마지막 단계에서 \(a_N\)을 조작하는 경우 3, 4 중 하나가 됩니다. \(N \le 2\)인 경우 \(a_N\)을 옮기지 읺으므로 따로 처리하지 않아도 됩니다.

\(N=3\) 또는 \(4\)일 때는 세 기둥의 상태를 같은 방향으로 만든 후 원반 2개를 옮기는 특수한 공식을 따라야 합니다.

void split(int s, int m, int e) { move(s, e); move(s, m); move(e, s); move(m, e); move(s, e); }

이제 상태가 같은 기둥끼리의 이동을 처리합니다.

inline void move(int s, int e);
inline void split(int s, int m, int e);

void hanoi(int n, int s, int m, int e, int state = 0) {
	if (n <= 0) return;
	if (n == 1) move(s, e);
	else if (((state >> s) & 1) ^ ((state >> e) & 1)) { .. } // 상태가 다를 때
	else if (((state >> s) & 1) ^ ((state >> m) & 1)) { // s와 e의 상태가 같고 m은 다른 상태
		if (n == 2) {
			move(s, m); move(s, e); move(m, e);
			return;
		}
		if (n == 3) {
			move(s, m);
			split(s, m, e);
			move(m, e);
			return;
		}
		else if (n == 4) {
			move(s, m); move(s, e); move(s, e); move(s, m);
			split(e, m, s);
			move(m, e); move(s, e); move(s, e); move(m, e);
			return;
		}
		hanoi(n - 3, s, e, m, state ^ (1 << s));
		move(s, e); move(s, e); // a_2, a_N 이동
		hanoi(n - 4, m, s, e, state ^ (1 << s | 1 << m));
		move(s, m); // a_1 이동

		hanoi(n - 2, e, m, s, state);

		move(m, e); // a_1 이동
		hanoi(n - 4, s, e, m, state ^ (1 << m | 1 << e));
		move(s, e); move(s, e);// a_N, a_2 이동
		hanoi(n - 3, m, s, e, state ^ (1 << e));
	}
	else { /**/ }
}

\(F’(n)=F’(n-2)+2F’(n-3)+2F’(n-4)+6\)이 되었습니다. 계산하기 귀찮은 꼴이 되긴 했지만 \(3^{N/2}\)보단 작겠죠.

Categories

BFS (10점)

하노이의 탑 (25점)

하노이의 탑, 근데 이제 원반 쪼개기를 곁들인 (26점)