백준 2260 - 핵폭탄

이번에 살펴볼 문제는 핵폭탄입니다. 꽤 오랫동안 아무도 풀지 못한 문제로 목록 상단에 남아있다가, 최근에야 풀렸습니다. 입력으로 폭탄의 위치와 \(N\)개 벽의 정보가 주어집니다. 목표는 최소 비용으로 폭탄을 완전히 둘러싸는 볼록 다각형 형태의 벽을 만드는 것입니다. 저도 문제는 읽어봤지만 어떻게 접근할지를 몰라 손 대지 못했는데, 동생의 간단한 풀이를 듣고 바로 구현했습니다. 이젠 내가 거꾸로 동생에게 배우고 있다는 게 좀 놀랍군요.

이번 문제를 풀기 전, 동생에게 추천받은 문제를 먼저 풀어보았고, 여기에 응용 가능하겠다는 생각을 했습니다. 임의의 점을 골라 최소 비용으로 연결하면서 특정 대상을 둘러싼 다각형을 만드는 데 최단 경로 탐색 기법을 활용할 수 있음을 미리 알고 있었고, 핵폭탄 문제에도 적용해보고자 했습니다.

하지만 최단 경로 탐색 기법을 단순히 적용하는 것으로는 이 문제의 조건을 만족할 수 없습니다. 완성되는 경로가 볼록 다각형이어야 하는데, 최소 비용으로 벽을 무작정 잇다보면 오목해질 수 있습니다.

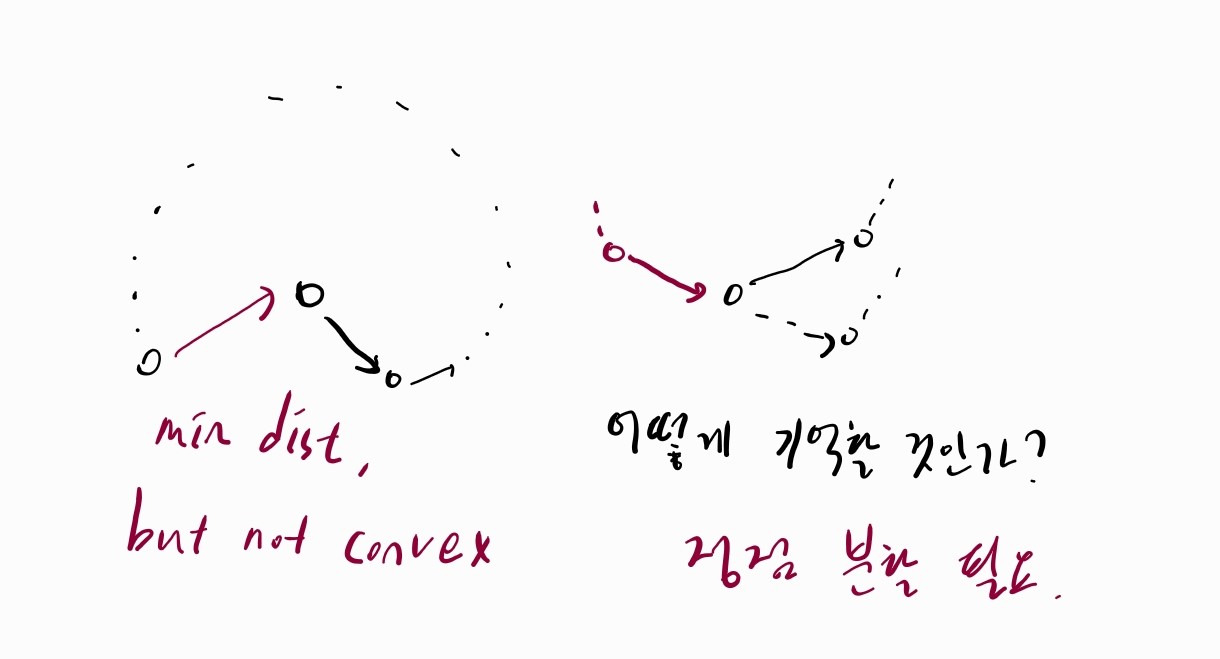
concave

이를 처리하려면 한 바퀴 돌아서 다시 시작 정점으로 진입할 때 경로가 볼록한지 확인해야 합니다. 아무런 장치 없이 최단 경로 알고리즘을 수행해서는 이를 알기 어렵고, 정점 분할을 통해 경로 정보의 일부를 갖고 있도록 해야 합니다.

발상은 어렵지만 간단한 아이디어로 이 문제를 해결할 수 있습니다. 바로 정점과 간선을 바꿔 생각하는 것입니다.

idea

간선에서 다음 간선으로 진행함은, 현재 간선의 시점에서 다음 간선의 시점으로 진행함과 동치입니다. 현재 시점 \(s_i\)에서 간선의 비용 \(C_i\)를 지불하고 다음 간선의 시점 \(s_j\)로 이동하도록 모델링합니다. 이제 기존의 정점-간선 관계를 갖는 최단 경로 탐색 기법을 적용할 수 있습니다! 게다가 한 점에서 만나는 여러 간선들에 대해 모두 정점 분할이 되어 있고, 각 정점은 사실 간선을 의미하므로 경로가 볼록한지 확인하기 위한 충분한 정보를 갖습니다.

이제 탐색 가능한 간선 쌍을 찾아봅시다. 볼록 껍질 내부 임의의 위치에 핵폭탄이 있다고 할 때, 모든 벽들은 폭탄의 위치를 기준으로 시점과 종점을 잡아줄 수 있습니다.

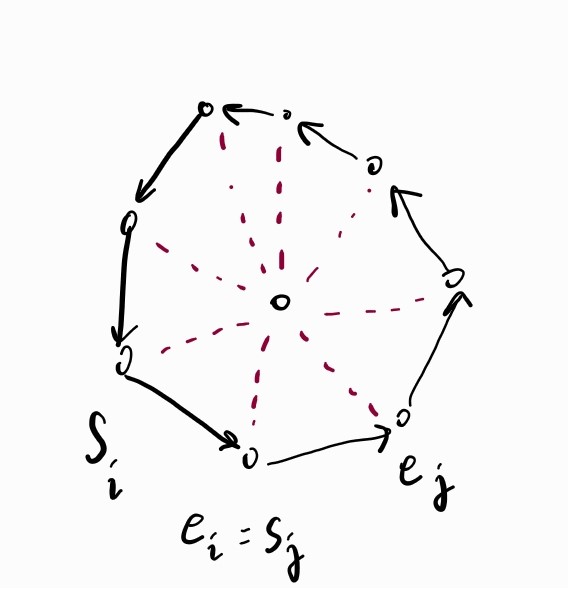
convex

간선 \(i\)에서 간선 \(j\)로 가기 위해서는 \(i\)의 종점과 \(j\)의 시점이 같고 두 간선이 볼록해야 합니다. 벽들의 수 \(N\)이 충분히 작으므로, \(O(N^2)\)으로 인접 행렬을 구할 수 있습니다.

나머지는 플로이드-워셜 등 최단 거리 알고리즘으로 정답을 구하면 됩니다.

use std::io::{self, BufRead};
use std::cmp::min;

static INF: i64 = 1e17 as i64;

struct Pos {
    x: i64,
    y: i64,
}

fn ccw(p1: &Pos, p2: &Pos, p3: &Pos) -> i64 {
   (p2.x - p1.x) * (p3.y - p2.y) - (p2.y - p1.y) * (p3.x - p2.x)
}

fn main() {
    let stdin = io::stdin();
    let mut iter = stdin.lock().lines();

    let s = iter.next().unwrap().unwrap();
    let v: Vec<i64> = s.split_whitespace().map(|x| x.parse().unwrap()).collect();
    let n = v[0] as usize;
    let pivot = Pos { x: v[1], y: v[2] };
    let mut edges: Vec<(Pos, Pos)> = vec![];
    let mut cost: Vec<i64> = vec![0; n];
    for i in 0..n {
        let s = iter.next().unwrap().unwrap();
        let v: Vec<i64> = s.split_whitespace().map(|x| x.parse().unwrap()).collect();
        let a = Pos { x: v[0], y: v[1] };
        let b = Pos { x: v[2], y: v[3] };
        if ccw(&pivot, &a, &b) > 0 { edges.push((a, b)); }
        else { edges.push((b, a)); }
        cost[i] = v[4];
    }
    let mut dist = vec![vec![INF; n]; n];
    for i in 0..n {
        for j in 0..n {
            if edges[i].1 == edges[j].0 && ccw(&edges[i].0, &edges[i].1, &edges[j].1) > 0 {
                dist[i][j] = cost[i];
            }
        }
    }

    for k in 0..n {
        for i in 0..n {
            for j in 0..n {
                let d = dist[i][k] + dist[k][j];
                if d < dist[i][j] { dist[i][j] = d; }
            }
        }
    }

    let mut ret = INF;
    for i in 0..n {
        for j in 0..n {
            ret = min(ret, dist[i][j] + dist[j][i]);
        }
    }
    if ret == INF { ret = -1; }
    println!("{}", ret);
}

Categories