백준 30372 - Convex Polygon MST

ICPC JAG 여름합숙캠프 3일차 문제 중 하나로 출제된 문제를 풀어보았습니다.

문제 자체는 간단합니다. 어떤 볼록껍질의 간선을 모두 지운 후, 정점들을 연결하여 최대 스패닝 트리를 만들 때, 연결된 간선 길이 제곱의 합을 구하면 됩니다.

만약 \(N\)이 충분히 작았다면 간선 가중치 테이블을 전부 순회하여 최대값을 찾을 수 있을 겁니다. 그 때의 시간복잡도는 \(N^2\)이고, 어렵지 않은 MST 문제가 되었을 겁니다. 하지만 \(N\)은 최대 \(120,000\)까지이므로 제한시간 내에 풀기는 불가능합니다.

그 특성상 프림이나 크루스칼 알고리즘은 간선 수에 크게 영향을 받을 수 밖에 없어서 이 문제에 적용하기는 쉽지 않습니다. 하지만 최소 스패닝 트리를 구하는 알고리즘은 또 있습니다.

보루프카 알고리즘

사실 이 방식이 MST를 구하는 다른 두 알고리즘보다 먼저 발표되었습니다만, 구현을 간단히 하고 핵심만 추려낸 두 알고리즘이 더 일반화되기는 했습니다. 최근 알고리즘 교재에선 프림과 크루스칼은 잘 보이지만 굳이 보루프카 알고리즘을 다루지는 않는 것 같더군요. 그런데도 굳이 이 문제에서 보루프카 알고리즘을 활용하고자 하는 이유는, 간선 수가 많지만 후보를 빠르게 찾을 수 있다면 충분히 MST를 빠르게 만들 수 있기 때문입니다.

알고리즘은 다음과 같습니다.

모든 트리에 대해, 다른 트리와 연결될 수 있는 최소 가중치 간선들을 찾는다.
최소 가중치 간선들에 대해 두 트리를 연결한다.
트리가 한 개라면 알고리즘을 종료하고, 아니라면 1번으로 돌아간다.

이 알고리즘의 시간복잡도 계산은 다음과 같습니다.

최초 \(N\)개의 트리가 존재한다. 트리 두 개씩을 연결하므로, 많아야 \(N/2\)개의 트리만 남는다. 그 다음은 \(N/4\), …이므로 연결 과정은 \(\log N\)번만 수행된다.

이제 해결해야 할 과제는 1번의 최소 가중치 간선을 찾는 과정의 시간복잡도를 줄이는 것입니다. 1번 과정의 시간복잡도를 \(T\)라 한다면, 전체 시간복잡도는 \(O(T \log N)\)이 됩니다.

보루프카 알고리즘을 활용하는 대표적인 문제로 XOR MST가 있습니다. 각 정점의 bit를 뒤집어 trie에 넣습니다. 트리의 깊이가 깊어질수록 하위 비트를 의미하는데, 어떤 노드가 왼쪽 자식과 오른쪽 자식을 둘 다 갖고 있다는 건 연결 간선이 필요하여 병합 비용이 발생함을 의미합니다. 트리의 각 깊이는 보루프카 알고리즘의 병합 스텝을 의미하는데, bit를 관리하는 trie의 최대 깊이는 \(\log N\)입니다. 어떤 깊이의 각 노드는 그 스텝에서 연결될 간선을 의미합니다. 이런 성질만 잘 알고 있다면 trie를 만든 후 DFS만 돌려줘도 정답을 구할 수 있습니다.

하지만 이 문제에선 trie를 쓸 수는 없으니, 다른 방법을 찾아야 합니다.

가장 먼 쌍 찾기

만약 가장 먼 쌍을 하나만 찾아야 한다면, 회전하는 캘리퍼스로 바로 해결할 수 있습니다. 하지만 이 문제에서 요구하는 것은 모든 트리에 대하여 가장 먼 트리를 찾아야 한다는 것입니다. \(N\)개의 서로 다른 트리를 비교하여 가장 먼 쌍 \(N\)개를 찾는 과정은 보통 \(O(N^2)\)입니다. 하지만 트리가 딱 2개 있을 때 가장 먼 정점 쌍을 빠르게 찾을 수 있다면 다음 방법을 고려해볼만 합니다.

분할 정복

힌트를 얻을 수 있는 문제로 동굴 탐험이 있습니다. 이 문제에서 핵심은, 1번 정점과 직접 연결된 정점들에 대하여, 최단 거리인 쌍을 빠르게 찾는 것입니다. 기막힌 분할 정복 방식으로 이를 해결할 수 있습니다. 다음과 같습니다.

1번 정점과 직접 연결된 정점들에 번호를 부여합니다.
번호의 각 비트에 대해, 0인 그룹과 1인 그룹으로 나누어 데이크스트라 알고리즘을 수행합니다.

비트로 그룹을 나누어 비교하면, \(\log N\)번의 비교만으로 \(N\)개 쌍의 최단 거리를 구할 수 있게 됩니다. 어떤 번호의 정점에 대해, \(\log N\)번의 비교 동안 다른 번호의 모든 정점은 상대 그룹에 적어도 한 번 포함됩니다. 모든 번호에 대해서도 마찬가지이므로 알고리즘이 성립합니다.

SMAWK

이제 남은 것은 두 그룹 간 가장 먼 정점 쌍을 찾는 것입니다. 어떤 거리 행렬 \(M\)에 대하여, \(M\left[ i, j\right]\)는 \(i\)번 정점과 \(j\)번 정점 간 가중치를 의미한다고 합시다. 문제는 모든 \(i\)에 대해 \(\max_{k = 0..N} M\left[ i, k\right]\)를 빠르게 찾는 것입니다. 거리 행렬에 아무런 규칙도 없다면 절망적이었겠지만, 다행히도 다음 규칙이 성립합니다.

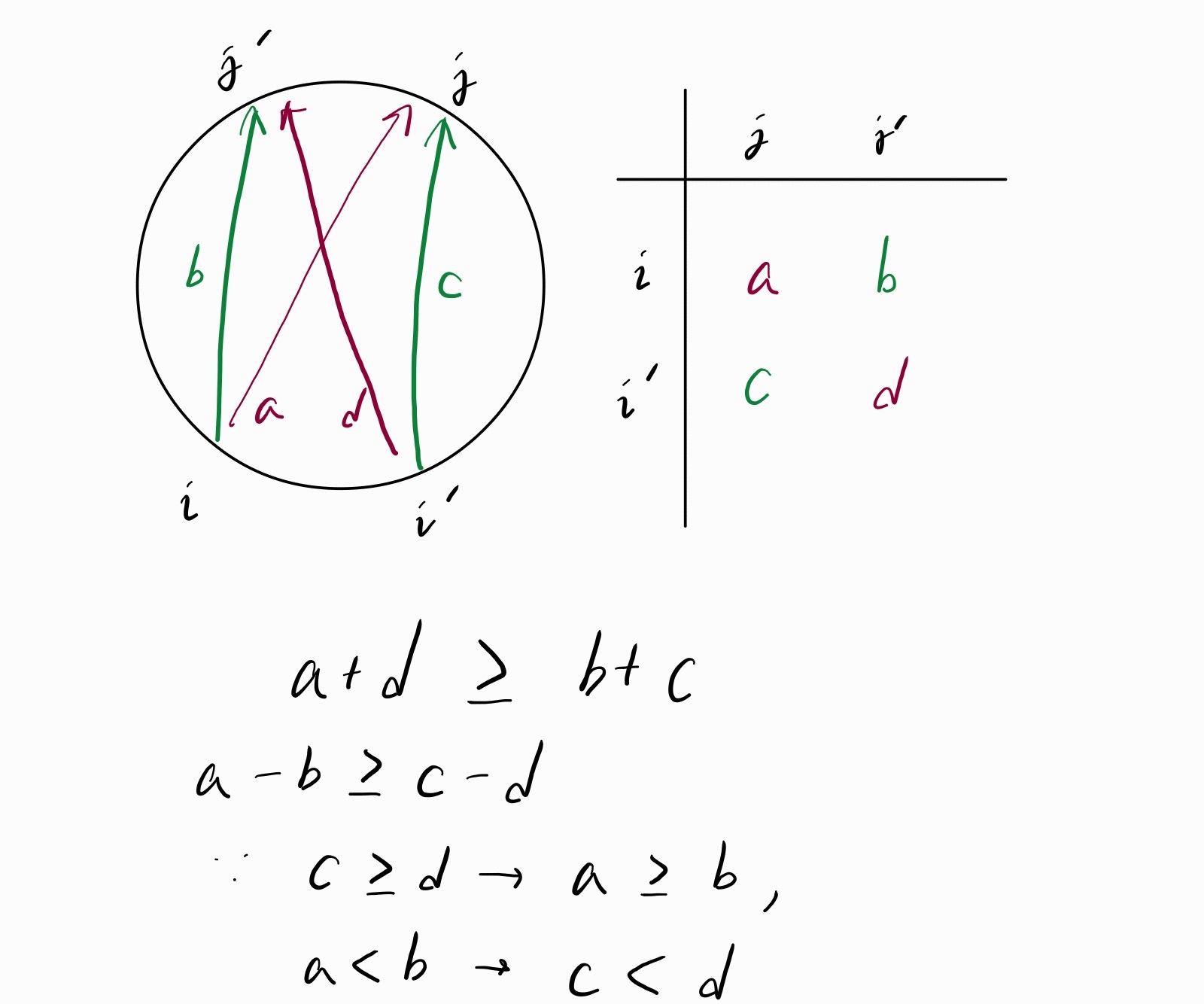
monotone

거리 행렬의 임의의 직사각형 모서리 4개를 가져와서 \(2 \times 2\) 행렬을 만들었을 때, 단조성이 관찰됩니다. 단조로운 행렬에 대해서는 분할정복 최적화, SMAWK 등의 알고리즘을 적용할 수 있습니다.

여기서 주의할 점은, \(i, i’, j, j’\)는 순서대로 위치해야 하며, 그 순서가 엇갈리게 되면 단조성이 깨지게 됩니다. 이를 해결하기 위해 왼쪽 밑의 삼각 부분을 오른쪽으로 옮겨주어야 합니다. 왼쪽 밑 삼각형과 오른쪽 위 삼각형은 단조성을 유지하면서 음수로 채워주겠습니다.

struct Pos {
	int i;
	ll x, y;
} pos[LEN];

ll distance(const Pos& a, const Pos& b) { return (a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y); }

ll f(int i, int j) { // 0 <= j < N * 2
	if (j < i) return -i -N +j;
	if (j >= N && j - N >= i) return -i -j;

	return distance(pos[i], pos[j % N]);
}

SMAWK 알고리즘을 통해 행렬의 각 행에서 최대 혹은 최소인 원소를 \(O(N+M)\)에 구해줄 수 있습니다. 구현은 이 논문을 참고했습니다.

ll smawk_maxima[LEN];

std::vector<int> smawk(const std::vector<int>& row, const std::vector<int>& col) {
	if (row.empty() || col.empty()) return {};
	if (row.size() == 1) { // linear search
		std::vector<int> ans = { 0 };
		int r = row[0];
		for (const int& c : col) {
			int ga = find(r), gb = find(c % N);
			ll dist = f(r, c);
			if (dist > smawk_maxima[r]) {
				ans[0] = c;
				smawk_maxima[r] = dist;
			}
			if (dist > target_dist[ga]) {
				target[ga] = gb;
				target_dist[ga] = dist;
			}
		}
		return ans;
	}

	// reduce
	std::vector<int> cols;
	for (const int& j : col) {
		if (cols.empty()) cols.push_back(j);
		else {
			int i;
			while (cols.size()) {
				i = cols.size() - 1;
				ll top = f(row[i], cols.back());
				ll next = f(row[i], j);
				if (top > next) break;
				cols.pop_back();
			}
			if (cols.size() < row.size()) cols.push_back(j);
		}
	}

	std::vector<int> rows;
	for (int i = 0; i < row.size(); i += 2) rows.push_back(row[i]);

	std::vector<int> ret = smawk(rows, cols);

	// linear search
	std::vector<int> ans(row.size());
	for (int i = 0; i < ret.size(); ++i) ans[i * 2] = ret[i];
	for (int i = 1, j = 0; i < row.size(); i += 2) {
		int s = ans[i - 1];
		int e = i + 1 < ans.size() ? ans[i + 1] : cols.back();
		int r = row[i];

		while (cols[j] < s) ++j;
		ans[i] = s;
		
		while (1) {
			int c = cols[j] % N;
			int ga = find(r), gb = find(c);
			ll dist = f(r, cols[j]);
			if (dist > smawk_maxima[r]) {
				ans[i] = cols[j];
				smawk_maxima[r] = dist;
			}
			if (dist > target_dist[ga]) {
				target[ga] = gb;
				target_dist[ga] = dist;
			}
			if (cols[j] >= e) break;
			++j;
		}
	}
	return ans;
}

이 문제를 풀면서 실수했던, 또는 놓치기 쉬운 것은 다음과 같습니다.

important

왼쪽 밑 삼각형을 오른쪽으로 옮기기 전의 인접 행렬은 totally monotone하지 않을 수 있다.
- \(i, j’, i’, j\)순으로 배치되는 경우가 있기 때문
비트 0, 1인 그룹을 나눈 후 축소된 배열의 왼쪽 밑과 오른쪽 위는 매끄러운 삼각형이 아닐 수 있다.
- 원본 배열은 유지한 채 살아남은 행과 열만 따로 처리할 필요 있음
왼쪽 밑과 오른쪽 위를 같은 값들(-INF, -1 등)로 채워넣을 경우 제대로 reduce되지 않을 수 있다. 행보다 열이 더 많은 경우 스택의 비교문이 의도한대로 동작하지 않는다.

// reduce
	std::vector<int> cols;
	for (const int& j : col) {
		if (cols.empty()) cols.push_back(j);
		else {
			int i;
			while (cols.size()) {
				i = cols.size() - 1;
				ll top = f(row[i], cols.back());
				ll next = f(row[i], j);
				if (top > next) break; // 여기가 문제
				cols.pop_back();
			}
			if (cols.size() < row.size()) cols.push_back(j);
		}
	}

이제 보루프카 알고리즘을 구현하면 됩니다.

void sweep(const std::vector<Pos>& a, const std::vector<Pos>& b) {
	std::vector<int> row, col;

	for (const Pos& p : a) row.push_back(p.i);
	for (const Pos& p : b) col.push_back(p.i);
	for (const Pos& p : b) col.push_back(p.i + N);
	smawk(row, col);
	memset(smawk_maxima, 0, sizeof smawk_maxima);

	row.clear(); col.clear();

	for (const Pos& p : b) row.push_back(p.i);
	for (const Pos& p : a) col.push_back(p.i);
	for (const Pos& p : a) col.push_back(p.i + N);
	smawk(row, col);
	memset(smawk_maxima, 0, sizeof smawk_maxima);
}

void solve() {
	memset(p, -1, sizeof p); // union-find

	// 정답 범위는 최대 1e24이므로 처리 필요
	ll large_part = 0, small_part = 0;
	std::cin >> N;
	for (int i = 0; i < N; ++i) std::cin >> pos[i].x >> pos[i].y, pos[i].i = i;
	int cnt = N;
	while (cnt > 1) { // O(log N)
		memset(target, -1, sizeof target);
		memset(target_dist, 0, sizeof target_dist);

		int bits = 0;
		while ((1 << bits) < N) bits++;

		for (int d = 0; d < bits; ++d) { // 그룹 나누기
			std::vector<Pos> a, b;
			for (int j = 0, k; j < N; ++j) {
				k = find(j);
				if (k & 1 << d) a.push_back(pos[j]);
				else b.push_back(pos[j]);
			} 
			sweep(a, b);
		}
		std::priority_queue<E> pq;
		for (int i = 0; i < N; ++i)
			if (i == find(i) && ~target[i])
				pq.push({ i, target[i], target_dist[i] });

		assert(pq.size());

		while (pq.size()) {
			E top = pq.top(); pq.pop();
			if (join(top.u, top.v)) {
				small_part += top.d;
				large_part += small_part / MOD;
				small_part %= MOD;
				--cnt;
			}
		}
	}
	if (large_part) {
		printf("%lld%017lld\n", large_part, small_part);
	}
	else printf("%lld\n", small_part);
}

상당히 비효율적인 곳이 많긴 합니다. 최적화는 취업 하고나서 해보죠.

Categories

보루프카 알고리즘

가장 먼 쌍 찾기

분할 정복

SMAWK