AtCoder Beginner Contest 351 후기

무직백수 노가다꾼의 최근 앳코더 참가 후기입니다.

다행히도 이번 컨테스트의 고난도 유형이 펜윅트리 정도라서 비교적 쉽게 풀 수 있었습니다. 800위 안에 들었고, 이제 레이팅은 1300점대가 되었습니다. 언제쯤 Blue가 될 수 있을까요. CodeForces Blue는 그런대로 쉬웠는데 앳코더는 민트를 벗어나지 못하고 있군요.

A, B는 단순 구현 문제니까 넘어가겠습니다.

C는 간단한 수학, 스택 응용 문제네요. 2의 거듭제곱 두 개를 더하는 것은 지수에 1을 더하는 것과 같으니 어렵지 않게 풀 수 있습니다.

D는 사방탐색 문제로 DFS든 BFS든 편한 걸로 구현하면 됩니다. 다만 자석에 인접한 칸이 중복으로 집계되는 문제에 대처해야 하는데, 이걸 해결하겠답시고 방문체크를 허술하게 해버리면 시간초과가 날 수 있으니 주의해야 합니다. 그냥 딱 그 정도 문제였습니다.

E는 사실 순서대로 풀다가 넘어갔습니다. F를 푼 뒤에 다시 풀 수 있었습니다. G번은 그냥 손도 안 대고 넘어갔습니다. 나중에 풀이를 보니 top tree를 쓰는 문제였더군요… link-cut tree에서 한 단계 더 높은 풀이가 ABC에서 나오다니, 이게 beginner 맞나 싶습니다.

F부터 보겠습니다. 구하고자 하는 것은 다음과 같습니다.

정수로 이루어진 수열 \(A = (A_1, A_2, … , A_N)\)에 대하여

\[\sum^N_{i-1} \sum^N_{j=i+1} \max(A_j - A_i, 0)\]

을 구하면 됩니다.

\(N\)이 충분히 작다면, \(O(N^2)\)로 풀 수 있습니다. 모든 순서쌍에 대해 max 값을 구하면 됩니다.

하지만 이 문제에서 \(N\) 제한은 400,000입니다. 더 빠른 풀이가 필요합니다. 조금 생각을 해보면, 다음과 같은 성질을 찾을 수 있습니다.

\(i \nless j\)인 \(A_i\)에 대해, \(A_j\)보다 값이 크다면 max 값은 0입니다.
\(A_i\)값이 \(A_j\)보다 작다면, 다음 식이 성립합니다.

\[\sum^{j-1}_{i=1} \max(A_j - A_i, 0) = C_jA_j-\sum_{A_i < A_j} A_i\]

단, 여기서 \(C_j\)는 \(A_i\)값이 더 작은 것들의 개수입니다.

두 개의 항을 빠르게 구해야 합니다. 세그먼트 트리, 펜윅트리 등을 쓰면 됩니다. \(A\)값들을 좌표압축 해준 후, \(j\) 순서대로 트리를 업데이트해가면서 \(A_j\) 값보다 왼쪽에 있는 수들의 개수와 합을 \(O(\log N)\)에 구할 수 있습니다.

typedef long long ll;
const int LEN = 4e5;

int N;

struct SegSum {
	ll t[LEN << 2];
	void update(int x, ll d, int s = 1, int e = N, int i = 1);
	ll get(int l, int r, int s = 1, int e = N, int i = 1);
} sum, cnt;

struct E {
	int a, i;
	bool operator<(const E& r) const;
} arr[LEN];

int A[LEN], order[LEN];

int main() {
	std::cin >> N;
	for (int i = 0; i < N; ++i) {
		std::cin >> A[i];
		arr[i].a = A[i];
		arr[i].i = i;
	}
	std::sort(arr, arr + N);

	int ord = 1;
	order[arr[0].i] = ord;
	for (int i = 1; i < N; ++i) { // 좌표 압축
		if (arr[i].a != arr[i - 1].a) ord++;
		order[arr[i].i] = ord;
	}

	ll ret = 0;
	for (int i = 0; i < N; ++i) {
		int x = order[i];
		ll S = sum.get(1, x - 1);
		ll C = cnt.get(1, x - 1);
		ret += C * A[i] - S; // 빠르게 계산하는 식
		sum.update(x, A[i]);
		cnt.update(x, 1);
	}
	std::cout << ret;
}

이 문제를 푼 후에야, E번에 접근할 힌트를 얻을 수 있었습니다.

체비셰프 거리

E번 문제에서 구해야 하는 것은 다음과 같습니다.

토끼는 대각선으로만 1칸 움직일 수 있습니다.
- 현재 위치가 (x, y)일 때, (x + 1, y + 1), (x + 1, y - 1), (x - 1, y + 1), (x - 1, y - 1) 중 한 칸으로 이동 가능합니다.
두 점 \(P_i, P_j\)에 대하여 토끼가 한 점에서 다른 점으로 이동하기 위한 최소 이동횟수를 \(dist(P_i, P_j)\)라 하겠습니다.
주어진 점들 \(P\)에 대하여,

\[\sum^{N-1}_{i-1} \sum^N_{j=i+1} dist(P_i, P_j)\]

를 구하면 됩니다.

일단 생각해볼 것은 다음과 같습니다.

과연 \(dist(P_i, P_j)\)는 무엇인가?

어떤 점에서 다른 점으로 대각선으로 이동하여 닿을 수 있는 최소 횟수는 적어도 두 점 간 x좌표 차이 또는 y좌표 차이보다는 같거나 클 겁니다. 좌표 차이를 \(dx, dy\)라 합시다. 만약 불필요한 움직임 없이 다른 점으로 최대한 가깝게 이동한다면, dist 값은 다음과 같이 됩니다.

\[dist(P_i, P_j)=\max(dx,dy)\]

몰랐는데, 이런 정의로 구하는 거리를 체비셰프 거리라 하더군요. 이제 수식을 다음처럼 변형할 수 있습니다.

\[\sum^{N-1}_{i-1} \sum^N_{j=i+1} \max(dx,dy)\]

수식이 F번과 비슷하게 생겼습니다. 나중에 설명하겠지만, 더 쉽고 간단한 방법이 있긴 합니다. 하지만 문제를 풀 당시에는 그걸 몰랐으니, 세그먼트 트리로 별 짓 다 해서라도 풀어야죠. 쩝…

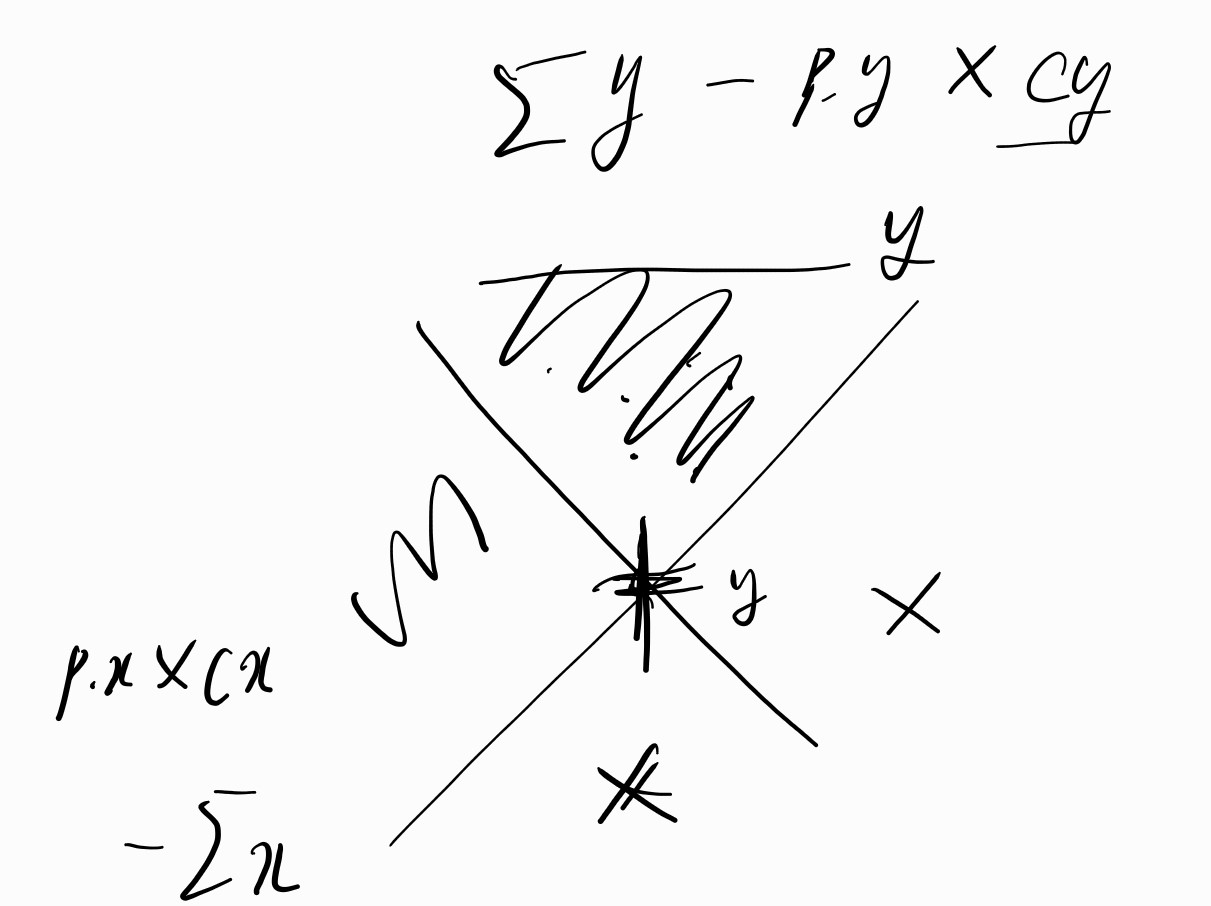
example

접근 방식은 이렇습니다.

점들을 왼쪽 위에서 오른쪽 아래로 정렬합니다.

엄밀한 정렬 기준은 다음과 같습니다.

  struct Pos {
          int x, y;
          int f() const { return y - x; }
          int g() const { return x + y; }
          bool operator<(const Pos& r) const {
              if (f() == r.f()) return x > r.x;
              return f() > r.f();
          }
      };

\(f\)는 우상향 직선을, \(g\)는 우하향 직선을 그리게 됩니다.

첫 번째 점부터 세그먼트 트리에 채워넣어가며 다음을 계산합니다.
- 어떤 점에 대한 \(g\)값을 기준으로 오른쪽에 있다면 \(dy\)값이 더 큰 점들입니다. 반대로 왼쪽에 있다면 \(dx\)값이 더 큽니다.
매번 점을 트리에 집어넣으면서 다음 값을 계산하면 됩니다.

\[\sum^{j-1}_{i=1} \max(dx, dy) = C_{x}P_j.x - \sum x + \sum y - C_{y}P_j.y\]

단, 여기서 주의할 점은 각 점들을 두 그룹으로 나눠 계산해야 한다는 것입니다. 체스의 흑칸 비숍과 백칸 비숍이 서로를 공격할 수 없는 것처럼, 두 그룹의 점들은 각각 홀수, 짝수로 나뉘어 따로 계산됩니다.

#include <iostream>
#include <algorithm>
#include <map>

typedef long long ll;
const int LEN = 4e5;

int N;

struct Space {
	int C;
	int X;
	std::map<int, int> order;

	struct Pos {
		int x, y;
		int f() const { return y - x; }
		int g() const { return x + y; }
		bool operator<(const Pos& r) const {
			if (f() == r.f()) return x > r.x;
			return f() > r.f();
		}
	} arr[LEN];

	struct SegSum {
		ll t[LEN << 2];
		void update(int x, ll d, int s, int e, int i = 1);
		ll get(int l, int r, int s, int e, int i = 1);
	} sumX, sumY, cnt;
	int el[LEN];

	ll solve() {
		ll ret = 0;
		for (int i = 0; i < C; ++i) {
			int ord = order[arr[i].g()];
			ll y = sumY.get(ord, X, 1, X);
			ll x = sumX.get(1, ord - 1, 1, X);
			ll cy = cnt.get(ord, X, 1, X);
			ll cx = cnt.get(1, ord - 1, 1, X);
			ll SY = y - arr[i].y * cy;
			ll SX = arr[i].x * cx - x;
			ret += SY + SX;

			sumY.update(ord, arr[i].y, 1, X);
			sumX.update(ord, arr[i].x, 1, X);
			cnt.update(ord, 1, 1, X);
		}
		return ret;
	}
} even, odd;

\(O(N \log N)\)으로 풀 수 있게 되었습니다.

한편 나중에 풀이를 봤는데 이런 유형의 문제가 나름 웰노운이라더군요… 좌표를 45도 변환하면 택시 거리를 대신 구하는 것으로 체비셰프 거리를 구할 수 있다고 합니다. 뭐 이런 게 다 있지? (사실 눈치채지 못하고 있었지만, 나중에 동생이 제 코드를 보면서 x + y, x - y 값을 쓰면서 45도 변환을 이미 하고 있었다고 하네요.) 다른 풀이는 여기서 자세히 설명하지는 않겠습니다.

Categories

체비셰프 거리