백준 19437 - Fantasia
구직 활동에 점점 자신이 없어지긴 하지만 계속 공부는 하고 있습니다. 이번에 푼 문제는 단절점을 찾는 알고리즘을 잘 응용하면 쉽게 풀 수 있어 포스팅해봅니다. 쉽다고는 했지만 실수를 꽤 많이 저지르는 바람에 삽질을 좀 하긴 했습니다.
어떤 무방향 그래프 \(G\)에 대해, 그래프의 가중치 \(z\)는 다음 식으로 계산됩니다.
- 어떤 연결 요소 \(H\), 각 노드의 가중치 \(w\)에 대한 가중치 \(z_H=\prod w\)
- 그래프 \(G\)의 모든 연결 요소 \(H\)에 대해 \(z=\sum z_H\)
\(i\)번 정점을 제거한 그래프 \(G_i\)의 가중치를 \(z_i\)라 할 때, \(\sum iz_i\)를 구하면 됩니다.
만약 모든 \(z_i\)를 따로 구하려고 한다면, 간단하게 DFS를 돌려서 풀 수 있을 것입니다.
ll dfs(int u) {
ll ret = W[u];
visited[u] = 1;
for (const int& v : g[u]) {
if (!visited[v])
ret = ret * dfs(v) % MOD;
}
return ret;
}
하지만 이렇게 풀면 \(O(N^2)\)이므로 시간초과를 피할 수 없습니다. 만약 어떤 점을 제거했을 때, 연결요소들이 어떤 식으로 떨어지는지 빠르게 알 수 있다면 모든 \(z_i\) 또한 빠르게 구할 수 있을 것 같습니다. 실제로 어떤 그래프의 모든 단절점은 \(O(N)\)으로 구할 수 있습니다. 이 과정은 그래프를 DFS로 탐색하는 순서대로 간선을 연결한 DFS 스패닝 트리의 사이클 유무를 확인하여 모든 정점의 단절점 여부를 판단합니다. 알고리즘을 설명해놓은 자료는 많기 때문에, 여기서는 문제 해설에 좀 더 초점을 두겠습니다.
전처리
우선 어떤 값들을 알 때 \(z_i\)를 빠르게 계산할 수 있을지 생각해봅시다. 그래프 \(G\)의 가중치 \(z\)는 DFS로 구할 수 있습니다. \(i\)번 정점을 포함하는 연결요소 \(H\)의 가중치 \(z_{H_i}\)또한 동일한 DFS로 구하면 됩니다. 하지만 이것들만 가지고는 부족합니다. \(i\)번 정점이 제거되었을 때, DFS 스패닝 트리의 자식 연결요소들은 기존의 연결요소에서 떨어져나갑니다. 이 때의 가중치 변화까지 한꺼번에 구할 수 있으면, 다음 식을 완성할 수 있습니다.
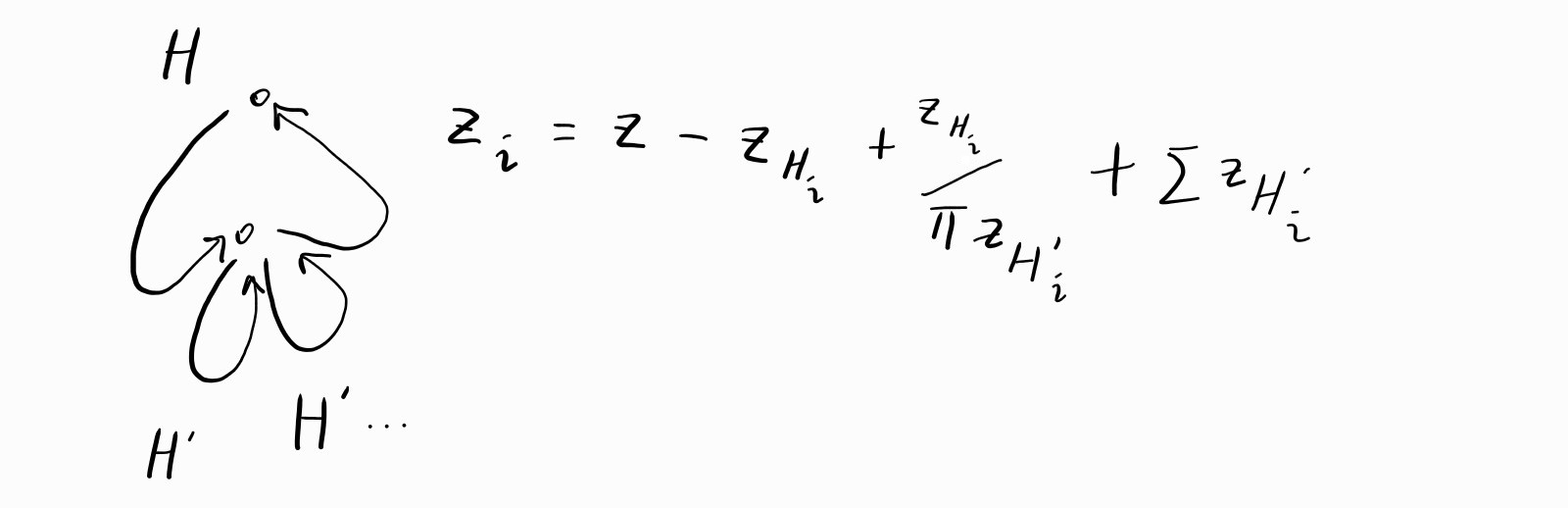
전처리로 모든 자식 연결요소들의 합과 곱을 미리 구해둔다면, \(z_i\)는 \(O(1)\)로 구할 수 있습니다.
- \(z_i\) 값은 전체 \(z\)에서 \(z_{H_i}\)를 뺀 후 부모 및 자식 연결요소 가중치들의 합을 더하여 구합니다.
- \(i\)번 정점의 부모 쪽 연결요소의 가중치는 \(z_{H_i}\)를 자식 연결요소의 곱으로 나눈 것과 같습니다.
단 한 가지 주의할 점은 만약 제거되는 정점 \(i\)가 연결요소 내에서 첫 번째로 방문한 정점일 때는 값이 조금 달라진다는 것입니다. 이 때는 스패닝 트리의 부모가 없으므로 \(1\)을 빼주어야 합니다.
이제 문제는 모든 자식 연결요소들의 가중치를 구하는 것입니다. 이는 정점 방문 순서에 따라 곱을 누적해가며 구할 수 있습니다.
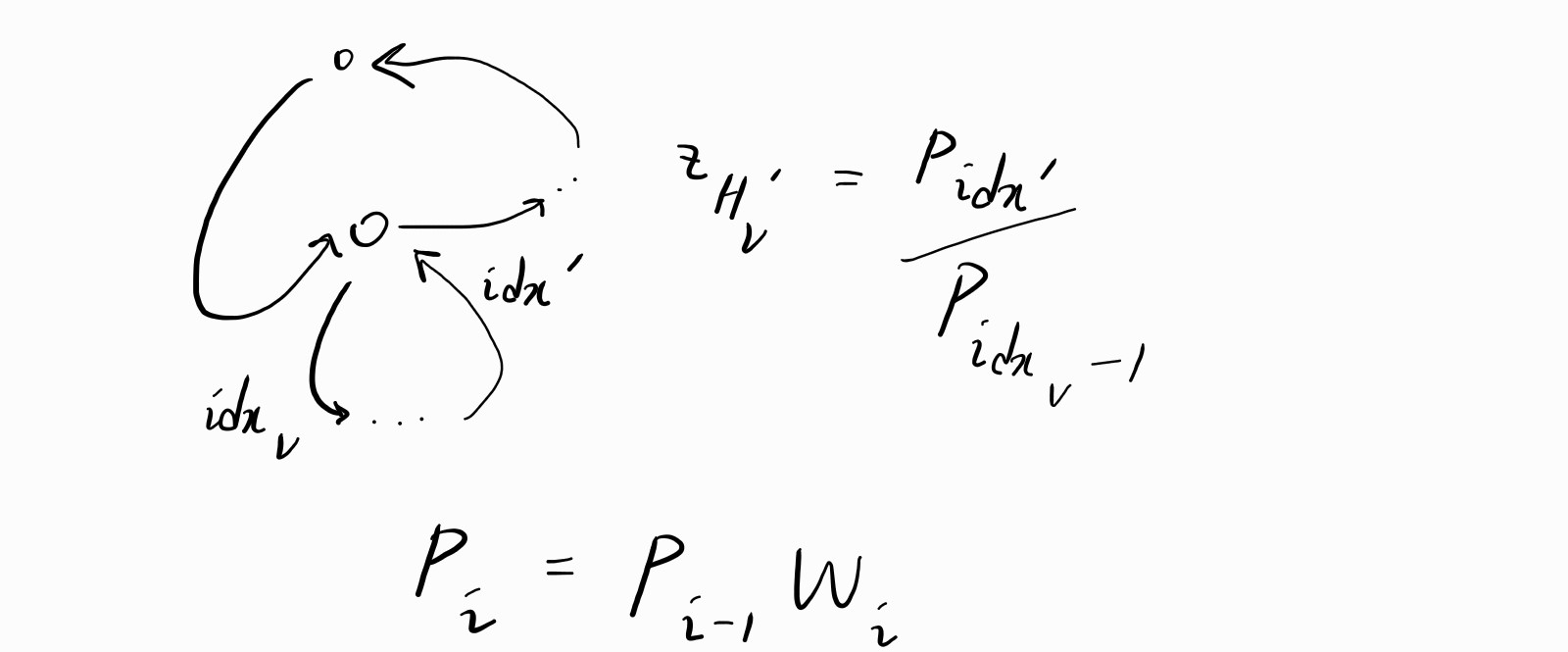
정점 \(u\)와 연결된 다음 정점 \(v\)를 방문하는 시점의 순서를 \(i_v\)라 하겠습니다. \(v\)로부터 탐색 가능한 모든 다음 정점을 방문하고 돌아왔을 때, \(u\)보다 먼저 방문했던 정점이 없다면 \(u\)는 단절점이 됩니다. 마지막으로 방문한 시점의 순서를 \(i’\)라 할 때, \(w_{i_v} w_{i_v+1} … w_{i’}\)는 자식 연결요소의 곱이 됩니다.
int dfs(int u, int p, int h) {
int m = ord[u] = ++idx;
Hs[u] = 0; Hp[u] = W[u];
P[ord[u]] = P[ord[u] - 1] * W[u] % MOD;
for (const int& v : g[u]) {
if (v == p) continue;
if (ord[v]) m = std::min(m, ord[v]); // 더 이른 시점을 방문. 사이클 존재
else {
int nxt = dfs(v, u, h);
if (nxt >= ord[u]) { // 더 이른 시점을 방문할 수 없음. articulation
ll sub = P[idx] / P[ord[v] - 1]; // ???
Hs[u] = (Hs[u] + sub) % MOD; // sum. 합
Hp[u] = (Hp[u] * sub) % MOD; // prod. 곱
}
m = std::min(m, nxt);
}
}
return m;
}
DFS 한 번만 돌리면 모든 자식 연결요소 가중치의 합과 곱을 빠르게 구해줄 수 있습니다. 하지만 여기서 한 가지 문제가 생기는데, 덧셈과 곱셈은 상관 없지만 나눗셈을 쓸 수 없다는 점입니다.
페르마 소정리
다행히도 이 문제를 해결할 수 있는 완벽한 방법이 있습니다. 놀랍게도 정수 연산에서 다음이 성립합니다.
\[1 \equiv k^{p-1} \pmod p\]여기서 \(p\)는 소수입니다. \(1,000,000,007\)은 소수이므로 위 식이 성립하고, 다음 또한 마찬가지입니다.
\[{1 \over k} \equiv k^{p-2} \pmod p\]이제 나눗셈을 대체하여 문제를 풀 수 있게 됩니다.
typedef long long ll;
const int LEN = 2e5 + 1;
const ll MOD = 1e9 + 7;
ll pow(ll a, ll b);
int dfs(int u, int p, int h) {
par[u] = p;
int m = ord[u] = ++idx;
H[u] = h;
Wg[h] = (Wg[h] * W[u]) % MOD;
Hs[u] = 0; Hp[u] = W[u];
P[ord[u]] = P[ord[u] - 1] * W[u] % MOD;
for (const int& v : g[u]) {
if (v == p) continue;
if (ord[v]) m = std::min(m, ord[v]);
else {
int nxt = dfs(v, u, h);
if (nxt >= ord[u]) { // articulation
ll sub = P[idx] * pow(P[ord[v] - 1], MOD - 2) % MOD; // P[idx] / P[ord[v] - 1]
Hs[u] = (Hs[u] + sub) % MOD;
Hp[u] = (Hp[u] * sub) % MOD;
}
m = std::min(m, nxt);
}
}
return m;
}
ll solve() {
...
ll S = 0;
for (int i = 1; i <= N; ++i) {
if (!ord[i]) {
Wg[++cc] = 1;
dfs(i, 0, cc);
S = (S + Wg[cc]) % MOD;
}
}
ll ret = 0;
for (ll i = 1, z, num; i <= N; ++i) {
num = Wg[H[i]];
z = (S - num + num * pow(Hp[i], MOD - 2) - !par[i] + Hs[i] + MOD) % MOD;
ret = (ret + i * z) % MOD;
}
return ret;
}
페르마 소정리를 쓰지 않고 풀 방법도 있을 것 같긴 한데, DFS 한 번으로 필요한 모든 항을 전처리하려면 이 방법 외에는 딱히 생각나지는 않습니다. 일단 취업이 먼저니까… 나중에 생각해봐야겠습니다.