백준 3383 - Submarines
원래 이 문제는 포스팅할 생각이 없었는데, 며칠 전 질문글에 답해주면서 최적화 아이디어가 떠올라 코드를 조금 손보게 되었습니다. 겸사겸사 포스팅도 하려고 합니다.
일단 문제를 파악해보죠. 바닷속에 여러 대의 잠수함이 순항 중입니다. 그 잠수함들은 나란히 줄을 서 순항하고 있으며, 각 잠수함들의 깊이는 서로 다릅니다. 잠수함이 신호를 보내면, 자신의 뒤에 있으면서 더 깊이 있는 것 중 가장 가까운 잠수함이 그 신호를 받습니다. 인접한 잠수함들끼리 순서를 바꾸는 일이 종종 일어난다고 할 때, 신호를 가장 많이 받는 잠수함을 찾을 수 있으면 됩니다.
왼쪽에서 오른쪽으로 잠수함들이 줄지어 있는데, 줄의 간격은 \(5\)km이고, 그 깊이 차이는 mm 단위입니다. 높이에 의한 거리 차이는 간격에 의한 차이보다 극도로 작고, 피타고라스 정리 등으로 증명하면, 빗변 거리를 실제로 구할 필요가 없음을 알 수 있습니다. 어떤 잠수함에서 신호를 보낼 때, 그 신호를 받는 잠수함은 오른쪽에 있으면서 더 깊은 것 중 가장 왼쪽에 있습니다.
만약 잠수함끼리 순서를 바꾸는 연산이 없다고 할 때, 신호를 받는 잠수함을 빠르게 찾는 문제는 완전히 오큰수 문제와 같습니다. 그리고 그 문제는 스택을 쓰면 \(O(N)\)으로 해결 가능합니다.
문제는 이걸 동적 쿼리로 해결할 수 있어야 한다는 건데요. 오큰수 문제에서 스택을 사용하지 않고 이 문제를 어떻게 풀 수 있을까 하는 질문글이 있었습니다. 실제로 중간에 값이 바뀌면 스택을 써서는 구할 수 없게 됩니다. 저는 이를 최댓값 세그먼트 트리로 해결했는데요, Submarines 문제를 풀 당시에는 세그먼트 트리 구간 쿼리와 이분탐색을 함께 쓴 \(O(\log^2 N)\) 방식이었습니다.
struct SegMax {
int seg_max[LEN << 2];
void update(int x, int d, int s = 1, int e = N, int i = 1) {
if (x < s || e < x) return;
if (s == e) { seg_max[i] = d; return; }
int m = s + e >> 1;
update(x, d, s, m, i << 1);
update(x, d, m + 1, e, i << 1 | 1);
seg_max[i] = std::max(seg_max[i << 1], seg_max[i << 1 | 1]);
}
int get_max(int l, int r, int s = 1, int e = N, int i = 1) {
if (r < s || e < l) return 0;
if (l <= s && e <= r) { return seg_max[i]; }
int m = s + e >> 1;
return std::max(get_max(l, r, s, m, i << 1), get_max(l, r, m + 1, e, i << 1 | 1));
}
} depth;
int get_rightmost(int i) {
int l = i + 1, r = N, m, j = N + 1;
while (l <= r) {
m = l + r >> 1;
if (depth.get_max(i + 1, m) > A[i]) {
j = std::min(m, j);
r = m - 1;
}
else l = m + 1;
}
return j;
}
이제 중간에 값이 바뀌더라도 오큰수를 비교적 빠르게 찾을 수 있게 됩니다. 시간 내에 해결은 가능하지만, 시간복잡도가 조금 아쉬운데요. 뭔가 다른 방법이 있지 않을까 생각은 하면서도 한 문제에만 매몰될 수는 없어 한동안 미뤄뒀습니다. 그런데 그 해답을 며칠 전 떠올렸습니다. 전처리된 구간 최댓값을 분할정복으로 확인하는 방법으로 \(O(\log N)\)이 가능했습니다.
struct SegMax {
int seg_max[LEN << 2];
void update(int x, int d, int s = 1, int e = N, int i = 1);
int nge(int x, int s = 1, int e = N, int i = 1) {
if (e <= x || seg_max[i] <= A[x]) return N + 1;
if (s == e) return s;
int m = s + e >> 1;
int l = nge(x, s, m, i << 1);
if (l <= N) return l;
return nge(x, m + 1, e, i << 1 | 1);
}
} depth;
방식은 단순합니다. 반으로 가른 구간 중 왼쪽에 오큰수가 무조건 있다면 오른쪽은 더이상 볼 필요가 없습니다. 구간을 반으로 갈라 들어가는 깊이는 \(\log N\)에 비례하므로 오큰수 쿼리를 더 빠르게 해결할 수 있습니다.
이제 남은 것은 자신을 오큰수로 하는 인덱스 집합을 관리하면서 이를 빠르게 분할, 병합하는 것입니다. Submarines 문제의 태그 분류가 스플레이 트리로 되어있는 이유가 바로 여기 있습니다.
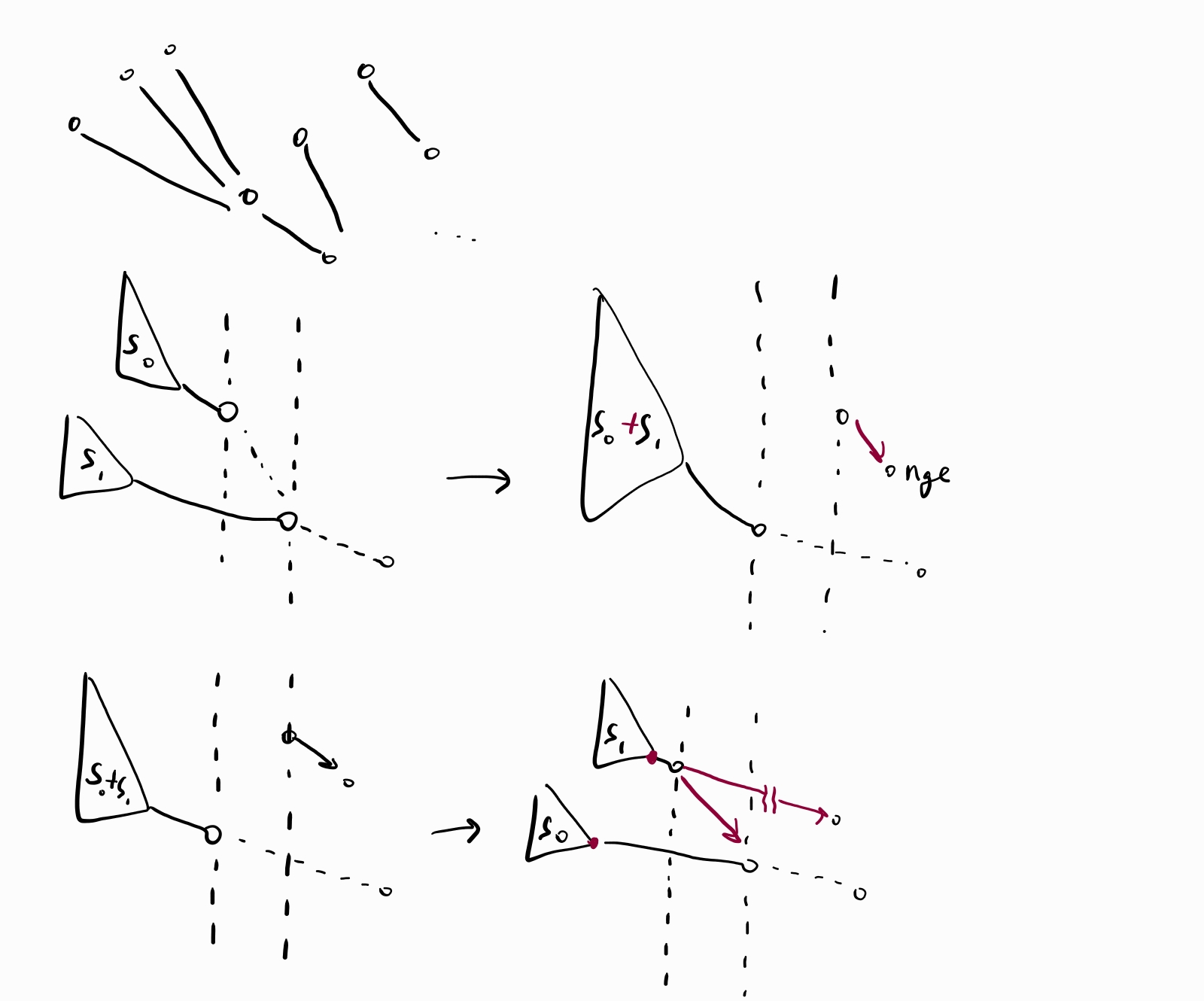
인접한 두 잠수함 중 어느쪽이 더 깊은가에 따라 연산이 달라지는데, 여기서 집합을 빠르게 처리하는 것이 관건입니다. 시뮬레이션 과정 최적화가 중요하기 때문에 ordered set이 기용된 것이고, 스플레이 트리 특유의 이상한 구간 쿼리가 나온다거나 하는 건 없습니다. 어쨌든 집합 처리를 제외하고 남는 것은 기존에 신호를 받던 잠수함이 앞으로 간 후 그 뒤에 있는 것들 중에서 신호를 받을 잠수함을 빠르게 찾는 연산입니다. 여기서 부분적인 최적화를 할 수 있었습니다.

뭐 큰 차이는 없습니다…