백준 18252 - 별이 빛나는 밤에

요즘은 동생과 함께 기하학 문제를 풀면서 부족한 부분을 채우고 있습니다. 이번에 푼 별이 빛나는 밤에는 꽤나 흥미로웠는데, 특히 접근과 증명은 어렵지만 비교적 간단한 코드로 최적화할 수 있다는 점도 한 몫 했습니다.

클래스 문제들을 밀면서 이것도 사실 꽤 오래전에 접하긴 했지만 삽화만 대충 보고는 냅다 도망쳤는데요. 동생이 문제를 풀더니 다시 한 번 제대로 읽어보라고 해서 그렇게 했죠. 위아래 별이 고정되어 있다는 조건이 있기 때문에, 레일은 사실상 고려할 필요가 없다는 것을 알 수 있었습니다.

맨 위의 점 \(U\)와 맨 아래 점 \(D\)를 잇는 선분 \(UD\)를 기준으로, 레일의 양 끝 중 가장 가까운 점을 고르기만 하면 됩니다. 만일 레일이 선분을 가로지른다면, 선분 위로 별을 올릴 수 있습니다. 임의의 다른 별을 골랐을 때, 선분 위에 있는 별은 \(U\) 또는 \(D\)를 골랐을 때보다 삼각형의 넓이가 항상 작으므로 제외할 수 있습니다. 레일이 어느 한 쪽에 있다면, 선분과 최대한 가깝게 하는 것이 삼각형의 면적이 작아집니다. 그렇게 선분과 가장 먼 레일의 별 \(P\)를 최적의 위치로 옮겨줍니다. 선분과 두 번째로 먼 레일의 별에 대해서, \(\triangle UDP\) 안에 들어갈 수 있다면 그 별은 제외할 수 있습니다. 그렇지 않다면 역시 최적의 위치로 옮깁니다. 이 과정을 반복하면 모든 별은 결국 선분에 가까운 쪽으로 모이게 됩니다.

#include <iostream>
#include <algorithm>
#include <vector>

typedef long long ll;
const int LEN = 1e4 + 2;

struct Pos {
    ll x, y;
    bool operator<(const Pos& p) const { return x == p.x ? y < p.y : x < p.x; }
    friend std::istream& operator>>(std::istream& is, Pos& p) { is >> p.x >> p.y; return is; }
} p[LEN];
ll cross(const Pos& p1, const Pos& p2, const Pos& p3) { return (p2.x - p1.x) * (p3.y - p2.y) - (p2.y - p1.y) * (p3.x - p2.x); }

int N, M;
std::vector<Pos> P;
Pos U, D;

int main() {
    std::cin >> N >> U >> D;
    P.push_back(U); P.push_back(D);
    for (int i = 0, y, xs, xe; i < N; ++i) {
        std::cin >> y >> xs >> xe;
        if (cross(U, D, { xs, y }) > 0) P.push_back({ xs, y });
        if (cross(U, D, { xe, y }) < 0) P.push_back({ xe, y });
    }
}

이제 가운데로 모은 별 중 3개를 골랐을 때 가장 큰 삼각형의 크기를 구하기만 하면 됩니다. 그냥 구하면 \(O(N^3)\)이므로 시간초과를 받게 됩니다. 여기서 간단한 기하학 지식과 또 간단한 최적화 기법을 적용하면 \(O(N^2)\)으로 아슬아슬 통과할 수 있는 풀이를 만들 수 있습니다.

일단 짚고 넘어갈 점은, 넓이가 최대가 되는 삼각형은 반드시 볼록 껍질 위에서 찾을 수 있다는 것입니다. 이걸 증명하는 논문도 있지만 아직 제대로 읽어보지는 않았습니다. 이제 볼록껍질 위에서 가장 큰 삼각형을 찾는 방법이 남았습니다.

\(O(N^2)\)

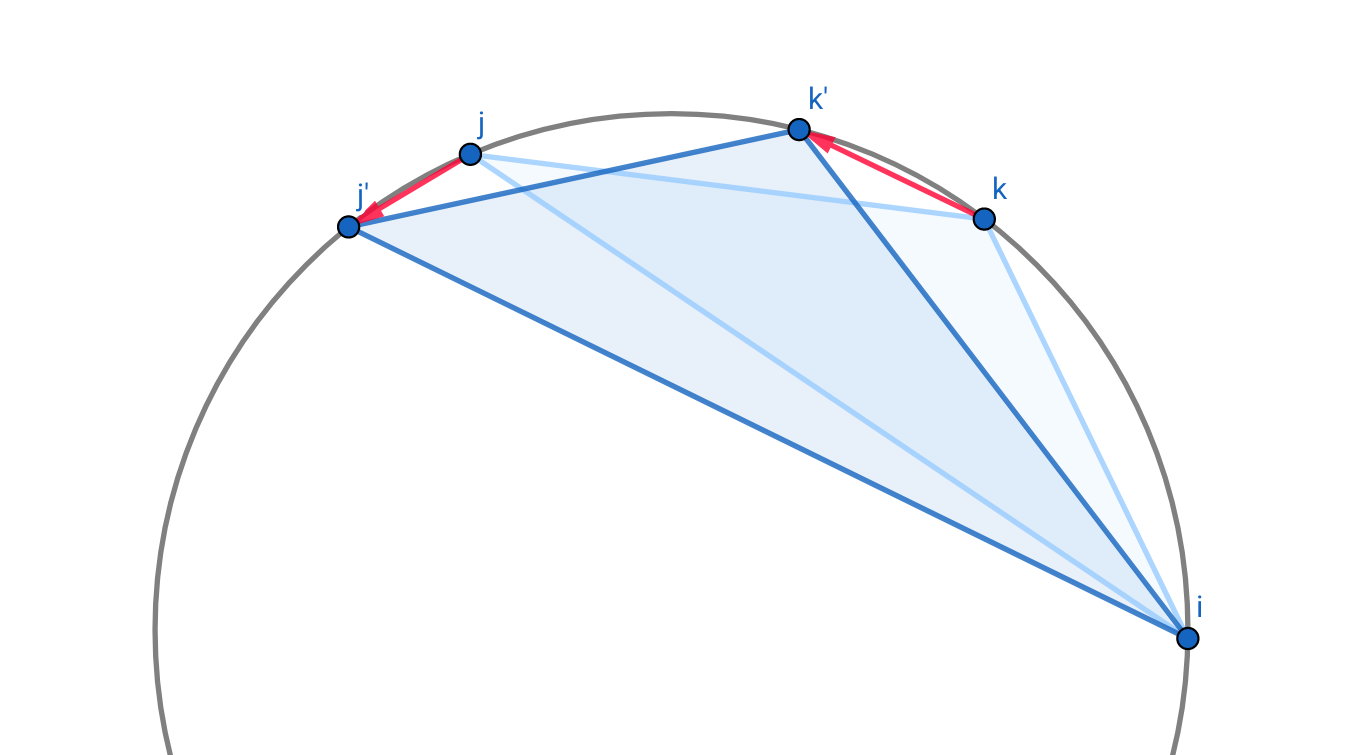
2-stable

볼록껍질의 임의의 점 \(i\)를 잡고, 그 다음 점을 \(k\), 그 다음은 \(j\)라 하겠습니다. \(\triangle ijk\)의 점 \(j\)를 앞으로 진행시키면, 최대 넓이가 되기 위해 \(k\)도 이동해야 합니다. 이 때, 새로 이동한 점 \(k’\)는 항상 \(k\)보다 앞에 위치합니다. 이전의 \(k\)의 위치를 기억할 수 있다면, 새로 이동한 점 \(j’\)에 대해 모든 \(k\)를 확인할 필요가 없습니다. 투 포인터를 활용하면 선형 시간 내에 점 \(i\)를 포함하는 가장 큰 삼각형을 찾을 수 있습니다. 그리고 모든 점 \(i\)에 대해 탐색할 경우 \(O(N^2)\)이 됩니다.

std::vector<Pos> P, H;

int main() {
    ...
    monotone_chain(P, H);

    ll ret = 0;
    for (int i = 0; i < M; ++i) {
        for (int j = (i + 2) % M, k = (i + 1) % M; j != i; j = (j + 1) % M) {
            while ((k + 1) % M != j && cross(H[i], H[(k + 1) % M], H[j]) > cross(H[i], H[k], H[j])) {
                k = (k + 1) % M;
            }
            ret = std::max(ret, cross(H[i], H[k], H[j]));
        }
    }
    std::cout << (ret >> 1) << '.' << (ret & 1) * 5;
}

사실 여기까지만 해도 충분히 정답이 되지만, 낭만이 없으니까… 더 줄여봅시다.

\(O(N)\)?

위 과정에서 조금 머리를 굴려보면 이런 생각을 할 수도 있습니다.

점 \(i\)도 다른 점들처럼 이동시키면 어떨까?

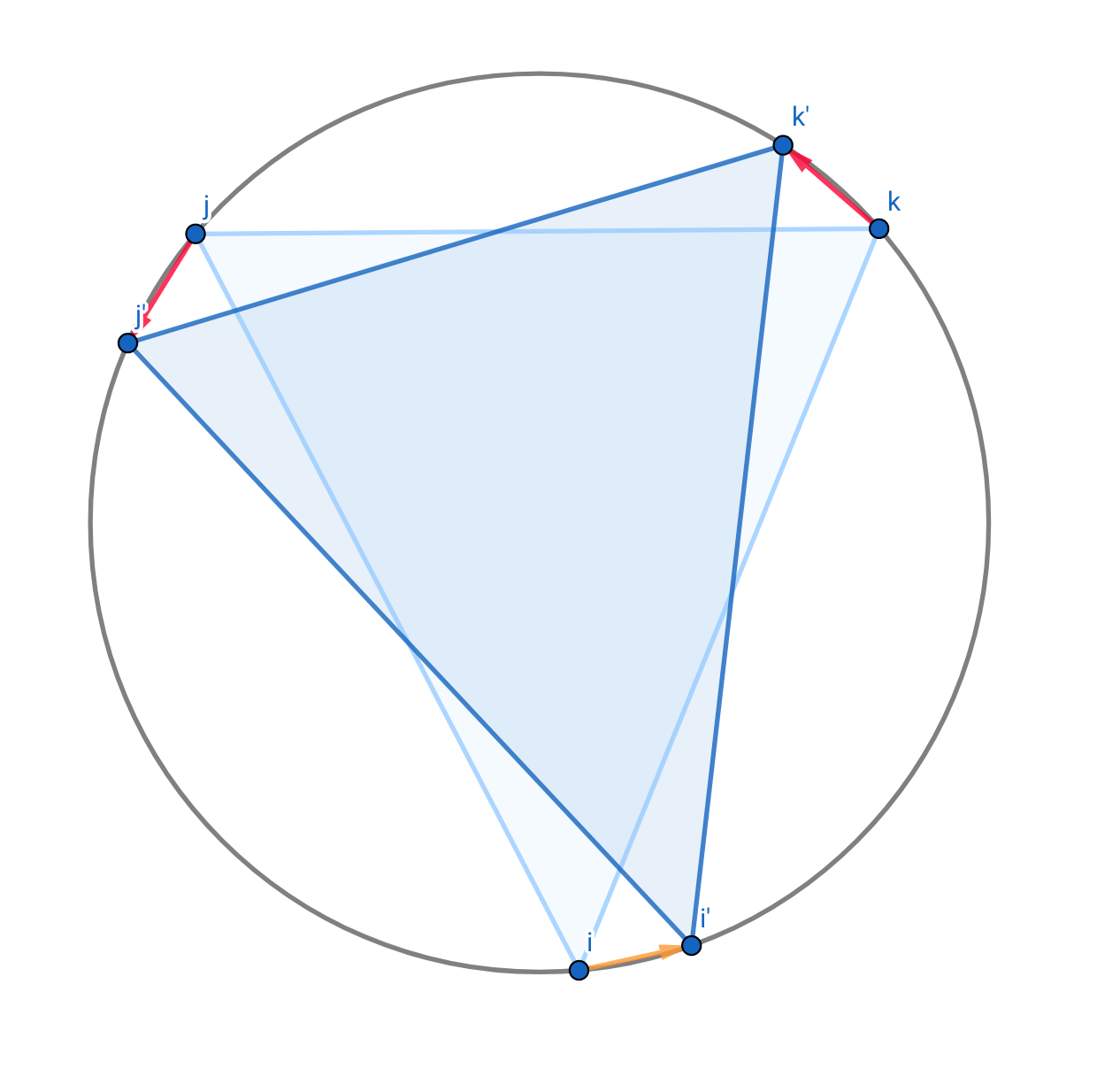
wrong

일단 용어 정리를 좀 해봅시다.

\(2\)-stable: 위 과정에서 점 \(i\)를 한 점으로 하는 삼각형들을 찾았는데, 이를 rooted at \(i\)라 하겠습니다. 그리고 나머지 두 점을 잡아서 어떤 한 점이라도 이동하게 되면 삼각형이 더 작아질 때 \(2\)-stable rooted at \(i\)이라 합시다.

anchored maximum: 점 \(i\)에 닻을 내리고 두 점 \(j\), \(k\)를 진행시키면서 넓이가 최대인 삼각형을 찾습니다. 두 점 중 어느 하나라도 움직일 경우 넓이가 작아질 때, 그 순간의 \(\triangle ijk\)를 anchored maximum이라 하겠습니다.

일단 움직일 수 있을 때까지 \(k\)를 움직입니다. 더 이상 \(k\)가 움직일 수 없거나 삼각형이 작아지면 \(j\)를 움직입니다. 그래도 삼각형이 작아지면 \(i\)를 움직여줍니다. \(i\)가 제자리로 돌아오면 알고리즘을 종료합니다. \(O(N)\)으로 모든 \(2\)-stable인 삼각형을 검사할 수 있다니! … 라고 생각할 수 있지만 사실 이 방식은 모든 anchored maximum을 검사할 뿐이며 임의의 점 \(p\)에 대한 최대 넓이인 \(2\)-stable rooted at \(p\)가 anchored maximum과 같다는 보장은 그 어디에도 없습니다. 실제로는 \(j\)가 더 이동해야 제대로 된 값이 나온다든지 하는 경우죠. 이 방식은 1979년 논문으로 알려진 후(Dobkin, Snyder) 얼마 지나지 않아 수많은 반례를 얻어맞고 반박되었습니다.

관련 논문(arXiv.1705.11035)에서 간단한 반례를 확인할 수 있고, 이를 대신하는 분할정복 알고리즘을 소개하고 있어 이를 구현해보기로 했습니다. (참고로 \(O(N)\) 방식도 최근 밝혀진 것 같은데, 이건 취업하고 나서 도전해야겠습니다.)

\(O(N \log N)\)

논문에서는 용어를 몇 개 더 정의합니다.

\(3\)-stable: \(\triangle ijk\)의 어떤 한 점이라도 이동하게 되면 삼각형이 더 작아질 때 이를 \(3\)-stable이라 합시다. 하나의 볼록껍질에 \(3\)-stable은 여러 개 존재할 수 있습니다.

interleave: 두 다각형의 각 정점들이 볼록껍질에서 번갈아 나타날 때, 두 다각형이 interleave 합니다. 삼각형 두 개가 서로 엇갈린 육망성 같은 모습을 생각하면 쉽습니다.

자세한 증명 전부를 여기다 쓰지는 않을 거고, 구현에서 핵심적인 몇 가지만 복습 차원에서 살펴보면 다음과 같습니다.

모든 \(3\)-stable은 서로 interleave 한다.
가장 큰 \(k\)-gon rooted at \(r\)은 largest \(k\)-gon과 interleave한다.

슬슬 현기증이 날 수준입니다. 하지만 실제 구현은 꽤 간단해지는데, 위 정리를 응용하면 다음 방식으로 분할 정복이 가능해집니다.

볼록 껍질을 largest triangle이 포함될 수 있는 절반 길이의 볼록 껍질 두 개로 나눌 수 있다.
재귀적으로 껍질을 계속 나누어 들어갈 수 있다.

dnc

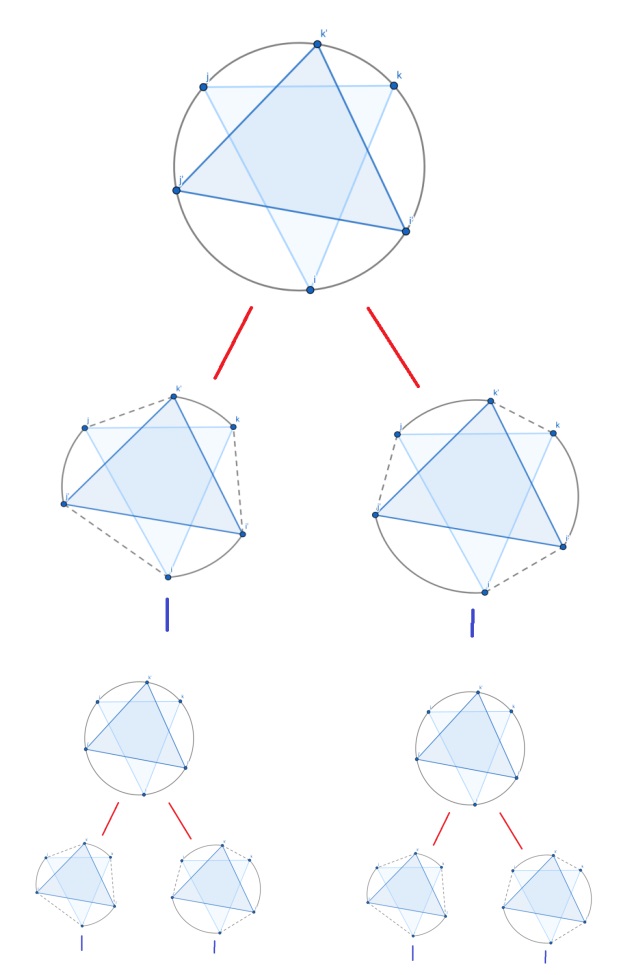
한 점 \(a\)를 잡고 maximum \(2\)-stable을 찾습니다. \(\triangle abc\)에서 인접한 두 점의 볼록껍질 구간 \(ab\)의 가운데 점 \(m\)을 찾고 \(2\)-stable rooted at \(m\)을 구해줍니다. 두 삼각형은 interleave하거나 그렇지 않을 수 있습니다. 두 삼각형의 점 6개는 볼록껍질을 6개 구간으로 나누고, 번갈아 나타나는 구간을 따로 모아 두 개의 볼록껍질을 만듭니다. 여기서 핵심은 가장 큰 삼각형은 위 정리들에 의해 두 개의 구간 중 하나에는 반드시 들어있다는 것입니다.

논문에서는 interleave 여부에 따라 부분 볼록껍질을 선택하는 방식이 다르긴 한데, 실제로는 6개 구간이 어떻게 나타날지 계산하는 것이 불필요한 재귀 호출을 가지치기하여 아낄 수 있는 비용 대비 번거롭다고 판단해서 그냥 무조건 둘 다 돌렸습니다. 또 구간이 분할되었을 때, 분할되기 전과 완전히 같은 껍질이 만들어지는 경우가 간혹 있습니다. \(2\)-stable의 두 점이 서로 인접하여 6개 구간의 길이가 들쭉날쭉해져 무한루프에 빠집니다. 만약 6개 구간이 일정하다면 항상 길이가 줄어들 것이고, 너무 긴 구간이 존재한다면 다음 재귀에서는 \(m\)으로 구간을 나누면 됩니다. 이를 해결하기 위해 매번 구간을 만들 때마다 볼록껍질을 돌려서 같은 결과가 나오는 것을 막았습니다.

typedef long long ll;
const int LEN = 1e4 + 2;

struct Pos {
	ll x, y;
	bool operator<(const Pos& p) const { return x == p.x ? y < p.y : x < p.x; }
	friend std::istream& operator>>(std::istream& is, Pos& p) { is >> p.x >> p.y; return is; }
} p[LEN];
ll cross(const Pos& p1, const Pos& p2, const Pos& p3) { return (p2.x - p1.x) * (p3.y - p2.y) - (p2.y - p1.y) * (p3.x - p2.x); }
ll dot(const Pos& p1, const Pos& p2, const Pos& p3) { return (p2.x - p1.x) * (p3.x - p2.x) + (p2.y - p1.y) * (p3.y - p2.y); }

void monotone_chain(std::vector<Pos>& p, std::vector<Pos>& hull) {
	std::sort(p.begin(), p.end());
	if (p.size() <= 2) {
		for (const Pos& pos : p) hull.push_back(pos);
		return;
	}
	for (int i = 0; i < p.size(); ++i) {
		while (hull.size() > 1 && cross(hull[hull.size() - 2], hull[hull.size() - 1], p[i]) <= 0) hull.pop_back();
		hull.push_back(p[i]);
	}
	hull.pop_back();
	int s = hull.size() + 1;
	for (int i = p.size() - 1; i >= 0; --i) {
		while (hull.size() > s && cross(hull[hull.size() - 2], hull[hull.size() - 1], p[i]) <= 0) hull.pop_back();
		hull.push_back(p[i]);
	}
	hull.pop_back();
}

struct Tri {
	int a, b, c;
	Tri& normalize() {
		if (a > b) std::swap(a, b);
		if (b > c) std::swap(b, c);
		if (a > b) std::swap(a, b);
		return *this;
	}
};
ll cross(const std::vector<Pos>& hull, const Tri& t) { return cross(hull[t.a], hull[t.b], hull[t.c]); }

Tri rooted_stable(const std::vector<Pos>& hull, int r) {
	int l = hull.size();
	Tri t = { r, (r + 1) % l, (r + 2) % l };
	for (int j = (r + 2) % l, k = (r + 1) % l; j != r; j = (j + 1) % l) {
		while ((k + 1) % l != j && cross(hull, { r, (k + 1) % l, j }) > cross(hull, { r, k, j })) {
			k = (k + 1) % l;
		}
		if (cross(hull, { r, k, j }) > cross(hull, t)) t = { r, k, j };
	}
	return t.normalize();
}

ll largest_triangle(std::vector<Pos>& hull) {
	int l = hull.size();
	if (l <= 50) { // 볼록껍질 길이가 충분히 작아지면 naive하게 찾습니다.
		ll ret = 0;
		for (int i = 0; i < l; ++i)
			ret = std::max(ret, cross(hull, rooted_stable(hull, i)));
		return ret;
	}
	Tri t0 = rooted_stable(hull, 0);
	ll ret = cross(hull, t0);

	int m = -1;
	int interval = 0;
	if (t0.b - t0.a > interval && t0.a + 1 < t0.b) m = t0.a + t0.b >> 1, interval = t0.b - t0.a;
	if (t0.c - t0.b > interval && t0.b + 1 < t0.c) m = t0.b + t0.c >> 1, interval = t0.c - t0.b;
	if (l - t0.c > interval && t0.c + 1 < l - 1) m = t0.c + l >> 1;
	Tri tm = rooted_stable(hull, m);
	ret = std::max(ret, cross(hull, tm));

	std::vector<Pos> p1, p2; // subpolygon
	int arr[7] = { t0.a, t0.b, t0.c, tm.a, tm.b, tm.c };
	std::sort(arr, arr + 6); arr[6] = 0;

	// 2-3, 4-5, 0-1 순으로 볼록껍질을 돌리면서 구간을 모아줍니다.
	for (int i = arr[2] + (arr[2] == arr[1]); i <= arr[3]; ++i) p1.push_back(hull[i]);
	for (int i = arr[4] + (arr[4] == arr[3]); i <= arr[5]; ++i) p1.push_back(hull[i]);
	for (int i = arr[0]; i <= arr[1]; ++i) p1.push_back(hull[i]);

	// 3-4, 5-0, 1-2 순으로 마찬가지로 해줍니다.
	for (int i = arr[3] + (arr[2] == arr[3]); i <= arr[4]; ++i) p2.push_back(hull[i]);
	for (int i = arr[5] + (arr[4] == arr[5]); i < l; ++i) p2.push_back(hull[i]);
	for (int i = arr[1]; i <= arr[2]; ++i) p2.push_back(hull[i]);

	std::vector<Pos>().swap(hull); // free memory
	ret = std::max(ret, largest_triangle(p1));
	ret = std::max(ret, largest_triangle(p2));

	return ret;
}

원래 알고리즘은 구간 길이가 3이 될 때까지 재귀적으로 탐색하지만, 실제 구간 분할 과정에서는 8 이하로 구간이 작아지게 되면 정점이 잘 제거되지 않는 치명적인 문제가 생겼습니다. 마치 육망성의 구간들이 번갈아가며 점멸하듯 무한루프에 빠집니다. 한편 \(N\)이 충분히 작으면 \(O(N^2)\) 알고리즘이 상수가 큰 \(O(N \log N)\) 알고리즘보다 부분적으로 더 좋은 성능을 보이므로, 적당한 크기의 RUN을 잡아서 해결했습니다.

여담으로 처음 코드를 작성하고 메모리 초과를 계속 받았는데요, 실제 알고리즘이 재귀적으로 들어갈 때 볼록껍질의 구간이 분리되면서 매번 새로운 공간 \(N\)을 사용하게 됩니다. 시간으로 따져서는 탐색에 그리 큰 문제가 되지 않지만, 이게 재귀로 들어가면서는 공간을 점점 많이 잡아먹게 되었습니다. 그래서 vector 메모리를 해제하려고 했는데, 이게 clear()나 resize(0)으로는 메모리가 해제되지 않더군요? 잘 알려진 swap trick이 있어 해결하긴 했는데 몰랐던 걸 하나 알아갔습니다.

Categories

\(O(N^2)\)

\(O(N)\)?

\(O(N \log N)\)