백준 25441 - 디지털 회로
이번에 풀어본 문제는 디지털 회로입니다. 문제를 이해하는 것부터가 쉽지 않고, 서브태스크도 조건이 상이하여 그다지 건질 게 없습니다. 리프 노드의 상태가 주어질 때, 루트가 1이 되는 경우의 수를 구하면 됩니다. 일단 몇 가지를 정의하고 넘어가겠습니다.
\(S_k\): 노드 \(k\)에 대해, 서브트리를 포함하여 가능한 모든 패러미터의 경우의 수.
\(dp_k\): 노드 \(k\)가 1이 되는 패러미터의 경우의 수.
우선 \(S_k\)는 구하기 쉬운데, 서브트리의 모든 정점 차수의 곱입니다. \(dp_k\)는 구하기가 꽤 까다로워보이는데요… 일단 결론을 내자면 임의의 리프 노드에 대해, 값이 1이 되었을 때 루트 노드에서 늘어나는 \(dp_0\)은 정해진 상수입니다. 좀 나이브하게 증명해보겠습니다.
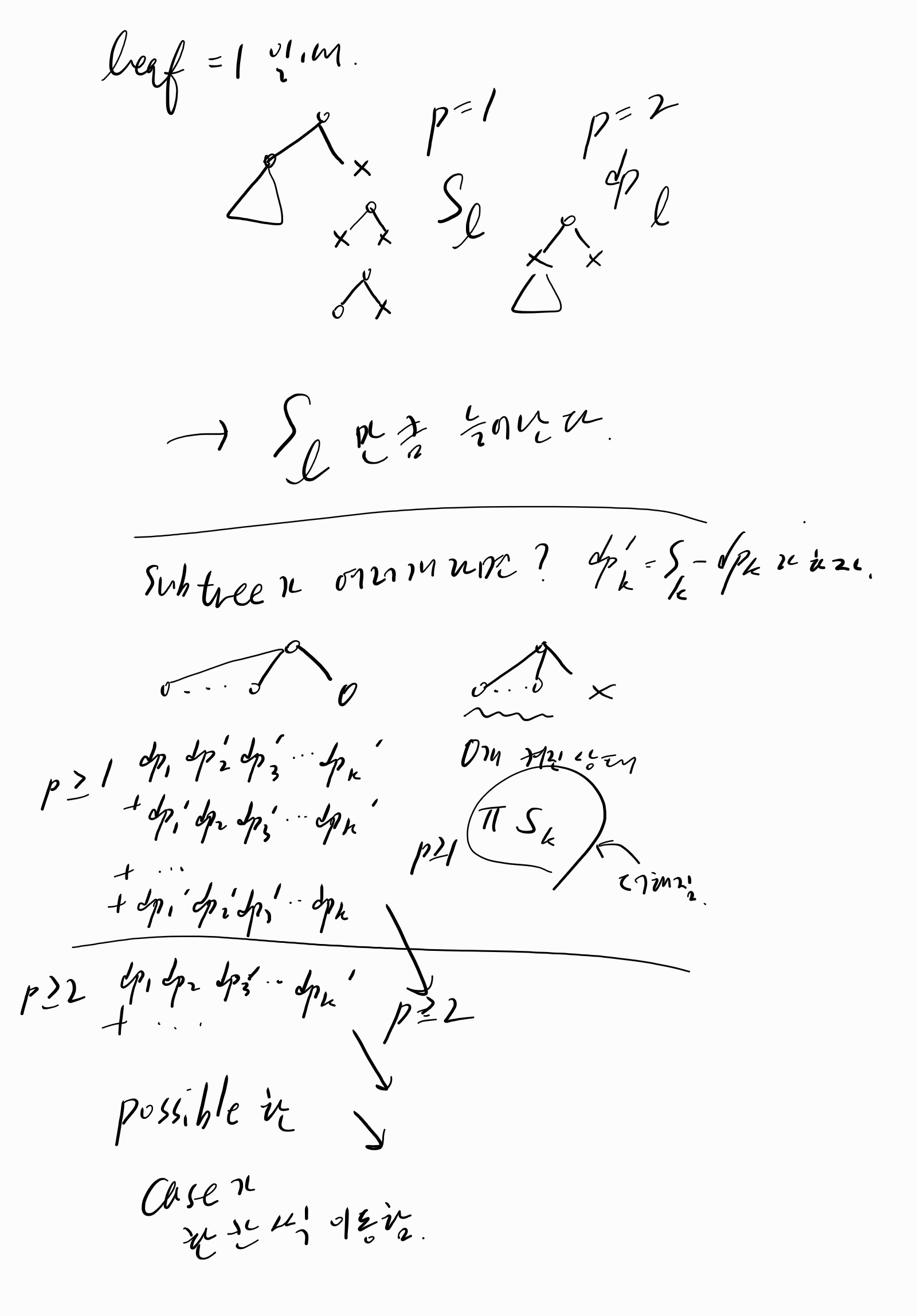
리프 노드가 바로 루트에 붙어있는 상황을 가정하겠습니다. \(S_i\)를 루트의 \(i\)번째 자식 노드까지를 포함하는 모든 패러미터의 경우의 수라 합시다. 리프가 마지막 \(k\)번째 노드라 하죠. \(P_k\)는 루트의 패러미터가 \(k\)일 때 1이 되는 경우의 수라 하겠습니다.
리프가 원래 0이었을 때의 경우의 수 \(dp_0\)은 \(k-1\)개 중 \(1\)개 이상 켜진 것 \(P_1\), \(2\)개 이상 켜진 것 \(P_2\), … \(k - 1\)개 이상 켜진 것 \(P_{k-1}\)들의 합입니다.
이제 리프 \(k\)의 값이 1이 되었다고 합시다. \(k\)개 중 \(2\)개 이상 켜진 경우의 수는, 리프가 0이었을 때 \(k-1\)개 중 \(1\)개 이상 켜진 경우의 수 \(P_1\)와 같습니다! 경우의 수들이 한 칸씩 이동하면서 값은 그대로 유지됩니다.
이제 문제는 루트의 패러미터가 1일 때의 값을 다시 계산해줘야 한다는 건데, 바로 이 부분이 문제를 해결할 열쇠가 됩니다. 리프 \(k\)의 값이 1이 되었기 때문에, 이전 \(k-1\)개 자식이 어떤 상태이든 상관없이 독립적으로 경우의 수는 \(S_{k-1}\)만큼 늘어납니다.

논의를 확장하여, 리프가 루트에 붙어있지 않은 상황까지 고려해도, 비슷한 논리로 리프가 1이 되었을 때 늘어나는 경우의 수를 계산해줄 수 있습니다.
계산해보면 임의의 리프 노드가 1이 되었을 때 늘어나는 경우의 수는 루트로부터 자신까지의 경로를 제외한 나머지 노드들에 대한 차수의 곱이 됩니다.
이건 dfs 두 번으로 모두 구해줄 수 있습니다.
typedef long long ll;
const int LEN = 100'001;
const ll MOD = 1e9 + 2022;
ll dfs1(int u) {
if (u >= n) return C[u] = 1;
ll c = 1;
for (const int& v : graph[u]) { // 오른쪽으로 훑습니다
l[v] = c; // 왼쪽 노드들의 경우의 수의 곱
c = dfs1(v) * c % MOD;
}
return C[u] = c * graph[u].size() % MOD;
}
void dfs2(int u, ll c) {
if (u >= n) { S[u - n + 1] = c; return; }
for (int i = graph[u].size() - 1, v; i >= 0; --i) { // 왼쪽으로 훑습니다
v = graph[u][i];
dfs2(v, c * l[v] % MOD);
c = c * C[v] % MOD; // 오른쪽 노드들의 경우의 수의 곱
}
}
구간 뒤집기는 세그먼트 트리같은 자료구조를 써주면 \(O(N + Q \log N)\)으로 해결 가능합니다.