백준 17169 - Eat Economically

외국이든 어디든 여행을 가면 맛집 찾아 다니는 걸 꽤 즐기는데, 이번 문제인 Eat Economically를 풀어보면서 옛날 생각도 나고 그렇네요. \(N\)일의 여행 동안 \(2N\)개의 메뉴를 겹치지 않게 점심 저녁에 한 번씩만 먹습니다. 그런데 하나의 메뉴라도 점심, 저녁 가격이 각각 다를 수 있습니다.(어째서?) 비용이 최소가 되게 하면 됩니다.

흠, 이거 곰곰히 생각해보면 약간 다르게 볼 수 있습니다.

\(2N\)명의 인부가 있고 두 개의 현장에 각각 \(N\)명씩 보내야 합니다. 인부는 각자 두 현장으로 이동하기 위한 비용이 다를 때, 그 비용을 최소로 하는 방법을 찾습니다. 이런 식으로 바꿔놓고 보니 할당 문제가 됩니다. MCMF로 모델링이 가능할 수 있다는 얘기가 됩니다.

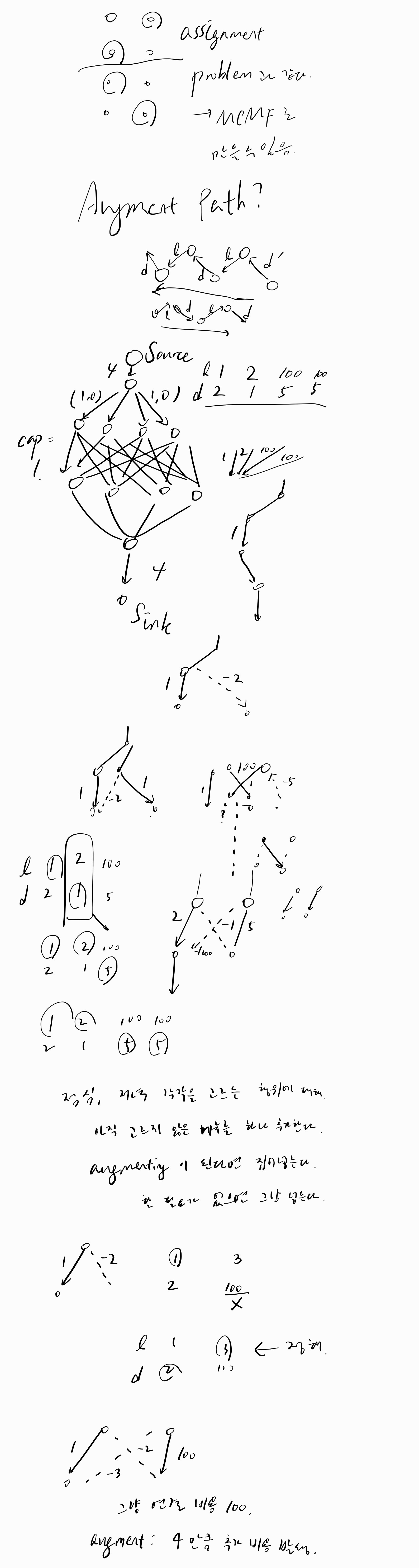
example1

그래프로 만들면 \(2N\)개의 메뉴 정점과 점심 정점 \(N\)개, 저녁 정점 \(N\)개가 생깁니다. 각각의 메뉴 정점은 점심 정점과 저녁 정점으로 각각 용량 \(1\), 비용은 \(l, d\)인 간선이 연결됩니다. 새 점심 메뉴를 하나 추가하는 것은 다음 과정으로 이루어집니다.

(Augmenting path를 찾을 수 없을 때) 비용이 \(l\) 증가하고 점심 간선에 용량을 \(1\) 흘립니다.
(Augmenting path를 찾았을 때) 기존에 저녁으로 흐르는 용량을 점심 간선으로 옮기고 비용 \(d\)로 저녁 간선에 용량을 \(1\) 흘립니다. 이 때 저녁 간선에서 점심 간선으로 옮기는 비용이 가장 작은 것이 우선합니다.

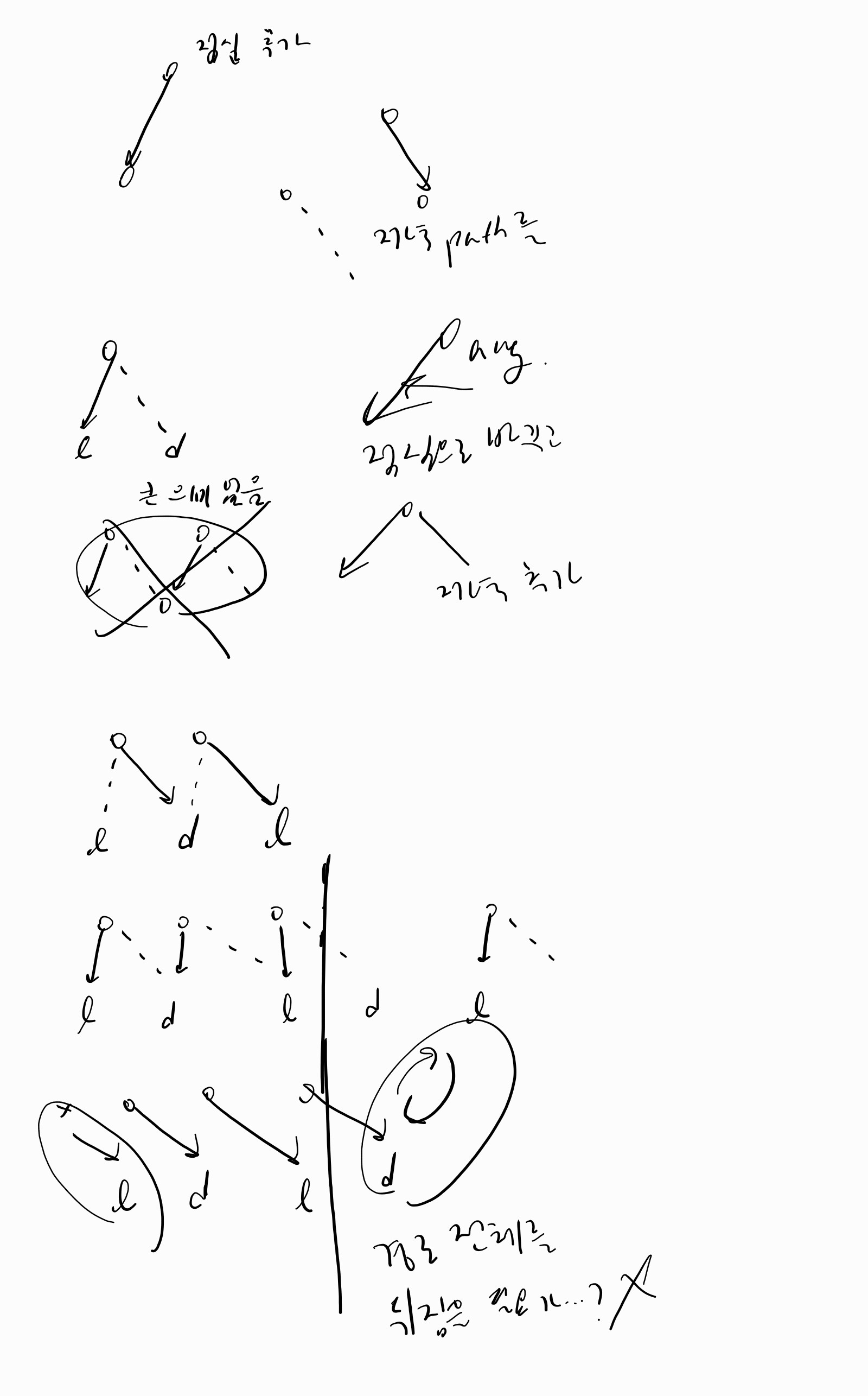
example2

통상의 Augmenting path는 간선이 번갈아가며 사용될 때 간선을 통째로 뒤집으면서 찾지만, 이 문제에서는 Augmenting path 전체를 굳이 뒤집을 필요가 없습니다. 애초에 모델링 될 때 점심 정점도 저녁 정점도 각각 \(N\)개씩 존재하므로 임의의 메뉴가 다른 메뉴에 종속적으로 연결되어있지 않습니다. (아무렇게나 뒤집어줘도 항상 완전 매칭 상태입니다) 비용이 가장 크게 줄어드는 메뉴 한 개만 뒤집어주면 됩니다.

typedef long long ll;
const int LEN = 200;

int N;

struct Menu {
	int x, y, i;
	bool operator<(const Menu& r) const {
		return x == r.x ? y < r.y : x < r.x;
	}
} lunch[LEN], dinner[LEN];

bool used[LEN];

std::priority_queue<ll> lq, dq;

int main() {
	std::cin >> N;
	for (int i = 0; i < N * 2; ++i) {
		std::cin >> lunch[i].x >> lunch[i].y;
		lunch[i].i = dinner[i].i = i;
		dinner[i].x = lunch[i].y;
		dinner[i].y = lunch[i].x;
	}
	std::sort(lunch, lunch + N * 2);
	std::sort(dinner, dinner + N * 2);
	ll cost = 0;
	for (int i = 0, l = 0, d = 0; i < N; ++i) {
		// lunch
		while (l < N * 2 && used[lunch[l].i]) ++l;
		while (d < N * 2 && used[dinner[d].i]) ++d;
		if (l >= N * 2 || l < N * 2 && d < N * 2 && lq.size() && dinner[d].x - lq.top() < lunch[l].x) { // augmenting path found
			used[dinner[d].i] = 1;
			ll aug = -lq.top(); // 저녁 하나를 점심으로 바꿀 때의 최소 비용
			lq.pop();
			cost += aug + dinner[d].x; // 저녁 메뉴 하나를 추가합니다.
			lq.push(dinner[d].x - dinner[d].y); 
			dq.push(aug);
		}
		else {
			used[lunch[l].i] = 1;
			cost += lunch[l].x; // 점심 메뉴를 추가합니다.
			dq.push(lunch[l].x - lunch[l].y);
		}
		// dinner
		...
	}
}

Categories