백준 2964 - 벽과 못

이번에 풀어볼 문제는 벽과 못입니다. 어떻게 접근할지만 알면 생각보다는 쉽지만, 거기까지 알아차리는 과정이 까다롭습니다. 문제는 요약하자면 볼록껍질에서 점을 하나씩 빼면서 그 다음 껍질을 구하고, 또 그 다음 껍질을 구합니다. 그렇게 점이 3개 남을 때까지 빼면서 넓이를 구하면 됩니다.

매 단계마다 볼록껍질을 구하면 \(O(N^2\log N)\)이므로 제한된 시간 내에는 해결이 힘듭니다. 뭔가 다른 방법을 찾아야 하는데, 볼록 껍질에서 점을 빼 나가는 것이 아니라 맨 마지막 단계에서부터 점을 하나씩 추가해나가면 시간을 조금 더 줄일 수 있습니다. 문제 조건 상 모든 점의 \(x, y\)좌표는 다르기 때문에 각 단계에서 빼야 하는 점은 유일하게 결정됩니다. 그렇다면 거꾸로 추가해나갈 점을 추적할 수 있습니다.

#include <iostream>
#include <algorithm>

typedef long long ll;
const int LEN = 300'000;

struct E {
	int i, A;
	bool operator<(const E& r) const { return A < r.A; }
} LR[LEN], UD[LEN];

struct Pos {
	int x, y;
} pos[LEN];

int N, L, R, U, D;
char S[LEN];
bool visited[LEN]; // 이전 과정에서 이미 빠진 못인지 체크합니다
int order[LEN];

int main() {
	std::cin >> N;
	for (int i = 0; i < N; ++i) {
		std::cin >> pos[i].x >> pos[i].y;
		LR[i] = { i, pos[i].x };
		UD[i] = { i, pos[i].y };
	}
	std::cin >> S;
	std::sort(LR, LR + N);
	std::sort(UD, UD + N);
	L = 0, R = N - 1;
	D = 0, U = N - 1;
	for (int i = 0; i < N - 2; ++i) {
		if (S[i] == 'L') {
			while (L <= R && visited[LR[L].i]) ++L; // 아직 빠지지 않은 왼쪽 점 찾기
			order[i] = LR[L].i; // i 번째에 빠지는 점을 찾았습니다
		}
		if (S[i] == 'R') {
			while (L <= R && visited[LR[R].i]) --R;
			order[i] = LR[R].i;
		}
		if (S[i] == 'D') {
			while (D <= U && visited[UD[D].i]) ++D;
			order[i] = UD[D].i;
		}
		if (S[i] == 'U') {
			while (D <= U && visited[UD[U].i]) --U;
			order[i] = UD[U].i;
		}
		visited[order[i]] = 1;
	}

	R = LR[0].i; L = LR[N - 1].i;
	U = UD[0].i; D = UD[N - 1].i;
	for (int i = 0; i < N; ++i) {
		if (!visited[i]) { // 빠지지 않은 점을 찾습니다.
			if (pos[i].x < pos[L].x) L = i;
			if (pos[i].x > pos[R].x) R = i;
			if (pos[i].y < pos[D].y) D = i;
			if (pos[i].y > pos[U].y) U = i;
		}
	}
}

이제 빠지는 순서의 반대로 점을 추가해주면 됩니다.

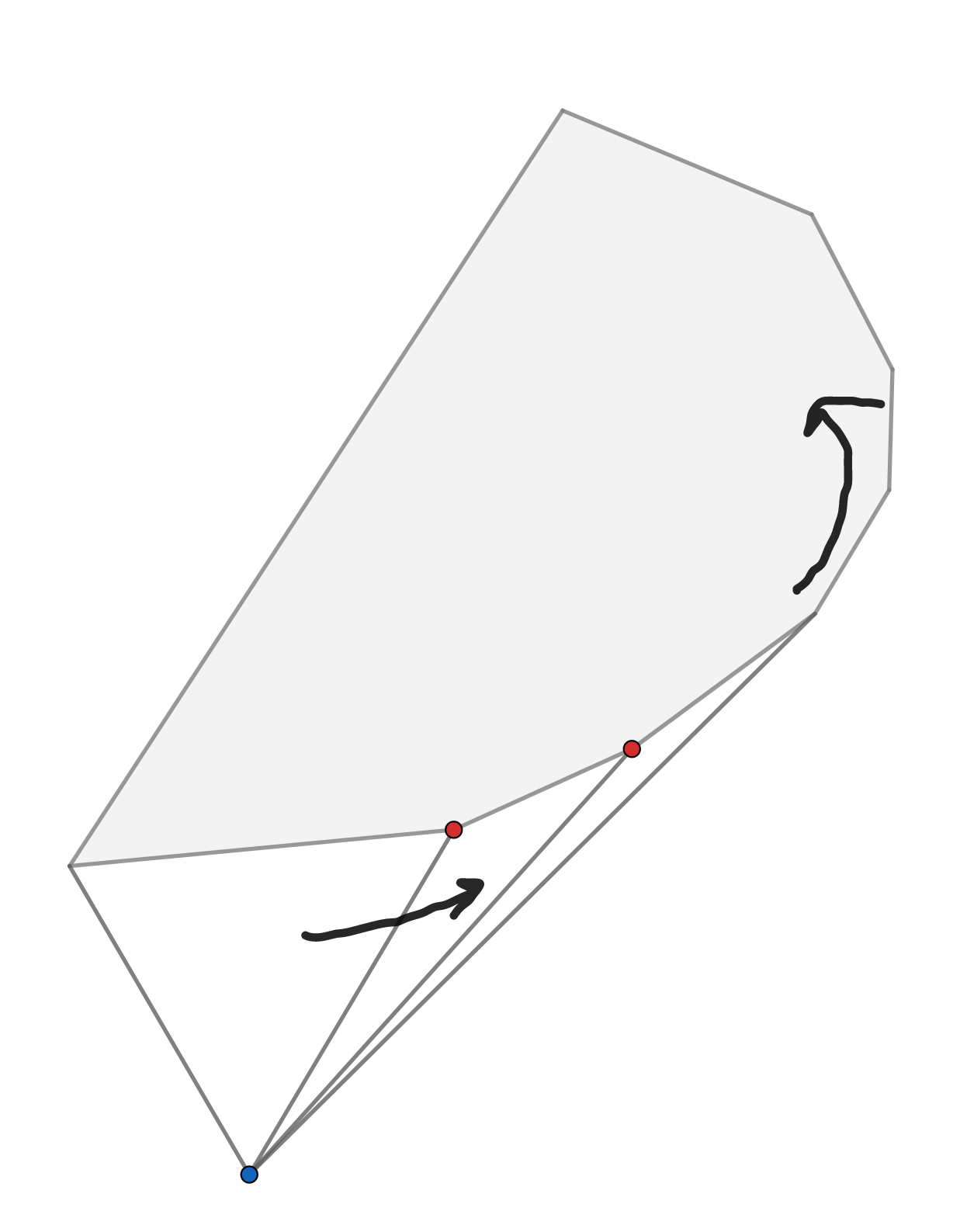
example

여기서 핵심은, 점을 추가하는 각 단계는 \(O(N)\)이지만 이걸 \(N\)번 반복했을 때의 시간복잡도가 \(O(N^2)\)가 되지 않는다는 것입니다.

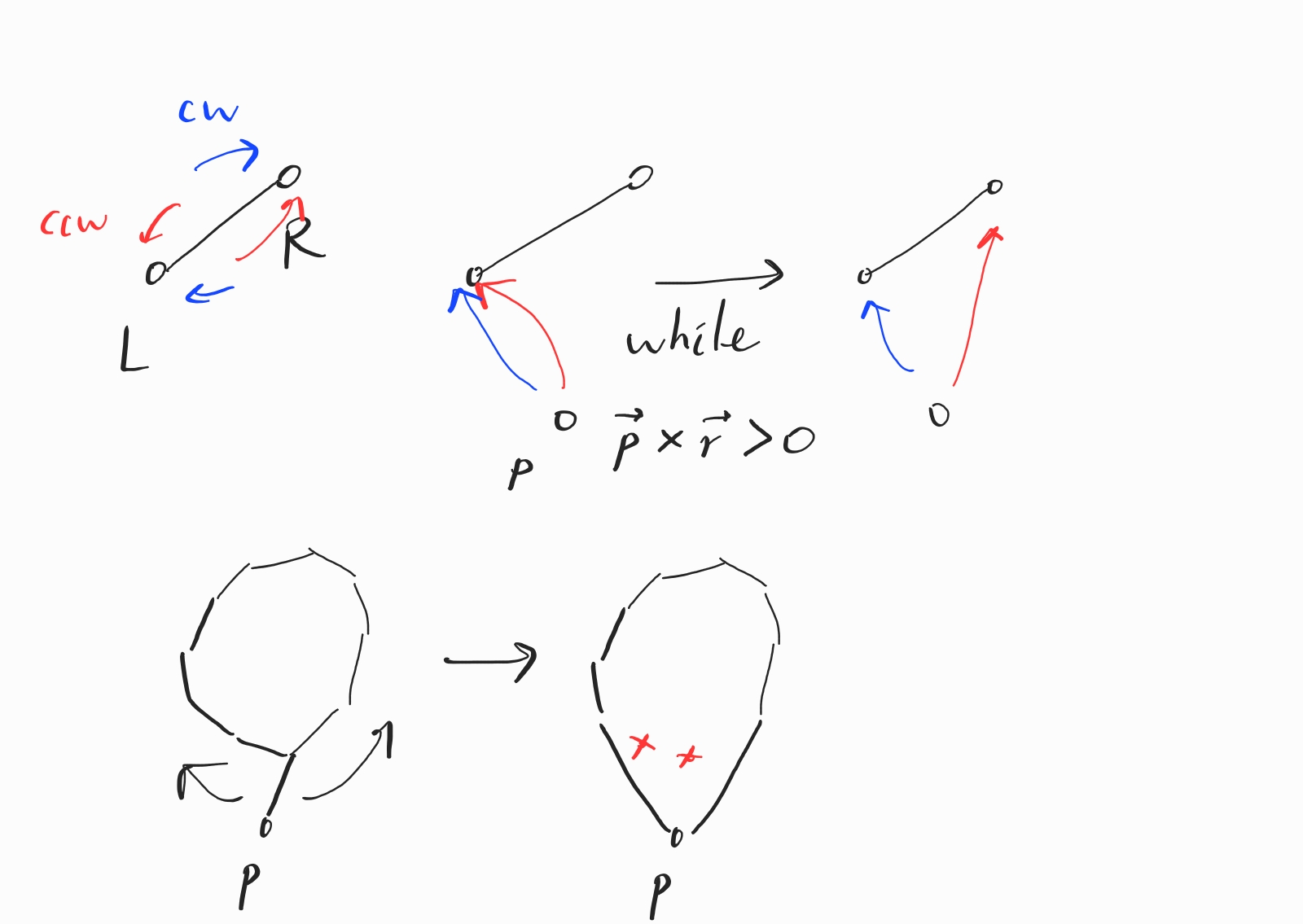
example

볼록껍질의 인접한 점은 연결리스트로 구현하여 임의의 원소 삽입, 삭제를 \(O(1)\)로 만들어줍니다. 새로운 점이 추가될 때, 일단 볼록껍질의 가장 가까운 점과 일단 연결합니다. 그리고 부채를 펴듯 양쪽으로 볼록껍질이 될 때까지 다음 원소를 찾아줍니다. 부채를 펴는 과정에서 볼록껍질에서 빠지는 점을 빨간색으로 표시할 때, 모든 단계를 완료하고 나서 빨간 점은 많아야 \(N-3\)개임을 알 수 있습니다.

...
struct Pos {
	int x, y;
	int cw, ccw; // linked list
} pos[LEN];
ll cross(const Pos& d1, const Pos& d2, const Pos& d3) {
	return (ll)(d2.x - d1.x) * (d3.y - d2.y) - (ll)(d2.y - d1.y) * (d3.x - d2.x);
}

int N, L, R, U, D;
char S[LEN];
bool visited[LEN];
int order[LEN];
ll ans[LEN];

int main() {
    ...

	pos[R].cw = pos[R].ccw = L;
	pos[L].cw = pos[L].ccw = R;
	for (int i = N - 3, j, k; i >= 0; --i) {
		if (S[i] == 'L') j = L;
		if (S[i] == 'R') j = R;
		if (S[i] == 'U') j = U;
		if (S[i] == 'D') j = D;
		k = order[i];

		ll area;
		pos[k].cw = pos[k].ccw = j; // 일단 가장 가까운 점과 연결합니다.
	
        // 반시계 방향이 볼록 껍질이 될 때까지 점을 빼줍니다. (외적 결과가 양수)
		while ((area = cross(pos[k], pos[pos[k].ccw], pos[pos[pos[k].ccw].ccw])) > 0) {
			ans[i] += area;
			pos[k].ccw = pos[pos[k].ccw].ccw;
		}
        // 시계 방향이 볼록 껍질이 될 때까지 점을 빼줍니다. (외적 결과가 음수)
		while ((area = cross(pos[k], pos[pos[k].cw], pos[pos[pos[k].cw].cw])) < 0) {
			ans[i] -= area;
			pos[k].cw = pos[pos[k].cw].cw;
		}
		pos[pos[k].ccw].cw = k;
		pos[pos[k].cw].ccw = k;

		if (pos[k].x < pos[L].x) L = k;
		if (pos[k].x > pos[R].x) R = k;
		if (pos[k].y < pos[D].y) D = k;
		if (pos[k].y > pos[U].y) U = k;

		ans[i] += ans[i + 1];
	}
	for (int i = 0; i < N - 2; ++i) std::cout << (ans[i] >> 1) << '.' << 5 * (ans[i] & 1) << '\n';
}

Categories