백준 - 오큰수
프로그래머스 스킬 체크 3단계 통과 후, 백준에 있는 문제들도 몽땅 정복해보기로 마음먹었습니다. (취업이 먼저인 것 같지만…) 이제 150개 정도 풀었네요. 단계별로 정복중인데, 어제까지 스택 다 풀고 이제 큐 문제 3개째입니다. 이번에 다뤄볼 주제는 오큰수입니다.
수열의 각 숫자들에 대하여, 자신의 오른쪽에 있는 수 중 자신보다 더 크면서 가장 왼쪽에 있는 수를 찾으면 됩니다. 오른쪽에 오큰수가 없으면 오큰수는 -1입니다. 예를 들어 수열 [3, 5, 2, 7]에 대하여, 오큰수 수열은 [5, 7, 7, -1]이 됩니다.
사실 이 문제는 별도의 조건만 없다면 굳이 복잡한 자료구조의 활용을 요구하지는 않습니다. 수열의 각 원소에 대하여 오른쪽을 훑다가 자신보다 더 큰 수가 나오면 그게 오큰수입니다. 이 때, 비교연산은 오른쪽에 있는 숫자들만큼 이루어지므로 최악일 때 평균 N / 2회 실행됩니다. 또한 모든 원소들에 대해 이루어지므로 시간복잡도는 N * (N / 2) = O(N2)입니다.
문제에서 주어지는 수열의 크기는 최대 106으로, 이중반복문을 활용한 오큰수 탐색의 최악 시간은 1012군요. 택도 없습니다. 다른 방법이 필요합니다.
문제의 카테고리가 스택이니, 이걸 써먹어볼 수 있을 것 같습니다. 그런데 어떻게 해야할까요? 수열을 맨 뒤에서부터 훑어본다면 어떨까요.
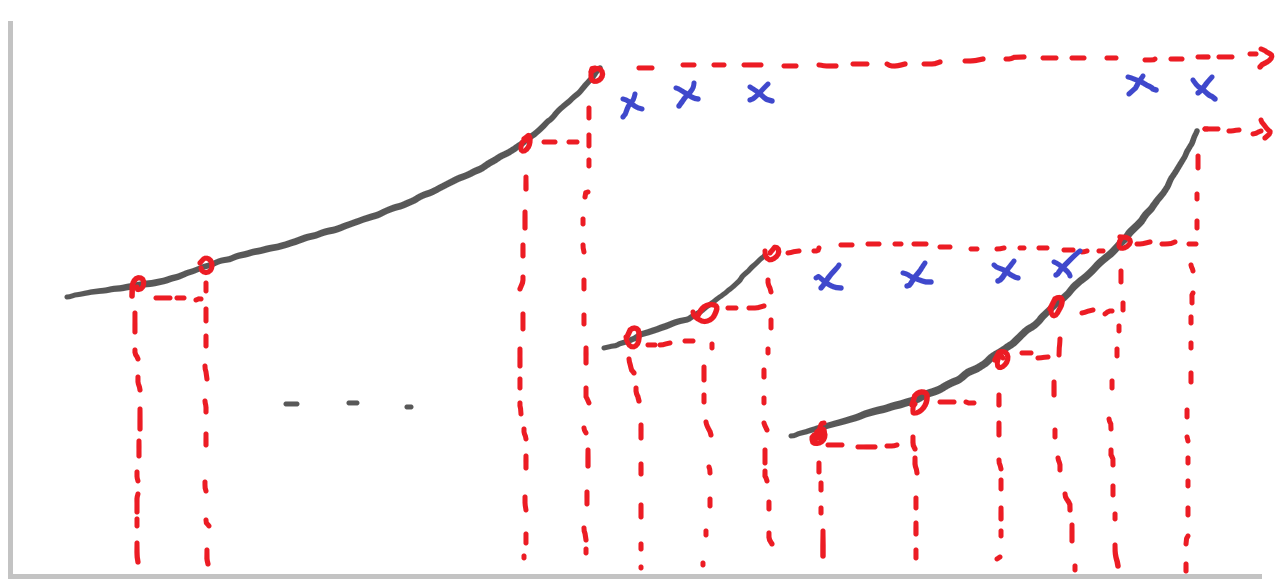
일단 맨 마지막 원소는 오른쪽에 수가 없으니 오큰수는 -1입니다. 그리고 이 수를 우선 기억해둡니다. 그 앞의 수를 끄집어내서 기억해둔 수와 비교합니다. 앞의 수가 더 작으니 오큰수는 바로 전의 수입니다. 앞의 수도 일단 기억해둡시다. 오큰수가 될 가능성이 있으니까요. 다시 앞의 수를 끄집어낸 후 맨 마지막으로 기억해둔 수와 비교하고 기억하는 이 과정을 반복합니다. 그러다가 앞의 수가 맨 마지막으로 끄집어낸 수보다 큰 상황이 생깁니다. 그러면 기억 속에서 앞의 수보다 작은 수들을 지우고, 앞의 수를 집어넣습니다. 그렇게 되면 기억해 둔 수들은 오름차순임을 보장할 수 있게 됩니다. 앞에서 끄집어낸 임의의 원소에 대해, 기억해 둔 오큰수 후보 중 앞에서부터 지워나가다보면 더 큰 수가 나오거나, 아니면 후보가 완전히 사라질 수도 있습니다. 그렇다면 이 수는 지금껏 나온 수들 중 가장 큰 수고, 오큰수는 -1이 됩니다.
무언가를 기억하기 위한 장치로써의 자료구조 중 위 절차에 가장 어울리는 건 뭘까요. 가장 마지막으로 기억해둔 수가 처음으로 튀어나와야 하는군요. 맨 처음 넣은 수는 마지막으로 나오게 됩니다. 후입선출(Last-In First-Out, LIFO), 이것이 스택입니다.
다시 위의 그림을 봅시다. 빨간 점으로 표시된 것을 절차 A, 파란 X 표시를 절차 B라 합시다. 절차 A는 뒤에서부터 원소를 끄집어 낸 후 순서대로 기억합니다. 절차 B는 기억해 둔 원소 중 끄집어낸 수보다 작은 숫자를 차례대로 지웁니다.
#include <iostream>
#include <stack>
int main() {
std::stack<int> stack, temp, result; int N, i;
std::cin >> N;
while (N--) std::cin >> i, stack.push(i); // 뒤에서부터 훑을 예정입니다. Stack에 넣읍시다.
while (!stack.empty()) {
N = stack.top(), stack.pop(); // 맨 뒤의 원소를 끄집어냅니다. (절차 A)
while (!temp.empty() && temp.top() <= N) temp.pop(); // 더 작은 수를 지웁니다. (절차 B)
if (temp.empty()) result.push(-1); // 기억해 둔 수가 모두 지워지면 오큰수는 -1입니다.
else result.push(temp.top()); // 더 큰 수가 있다면, 그 수가 오큰수입니다.
temp.push(N); // 끄집어낸 수를 기억해둡니다.
}
while (!result.empty()) std::cout << result.top() << '\n', result.pop();
}물론 배열과 인덱싱으로 오큰수를 담아둘 수도 있지만, 어차피 스택을 활용해 순차적으로 풀어나가는 거라면, 초기화할 자료도, 결과를 담을 자료도 스택에 담아 취급할 수 있습니다. 위 예제에서는 배열 없이 스택 3개로 풀었습니다.