KMP 알고리즘

동생한테 KMP 알고리즘을 설명해주다가, 속 시원하게 가르쳐주는 글이 별로 없는 것 같아서 하나 포스팅합니다.

문자열 알거리즘 중에서도 KMP는 그 난해함 때문에 악명이 높습니다. 교수님이 설명도 안 하고 넘어간다, 봐도봐도 뭔지 모르겠다… 사실 KMP 알고리즘을 처음부터 제대로 이해하고 넘어가기 위해서는 전혀 상관 없어보이는 것부터 시작해야 합니다.

유한상태기계

유한상태기계(Finite State Machine)가 무엇일까요?

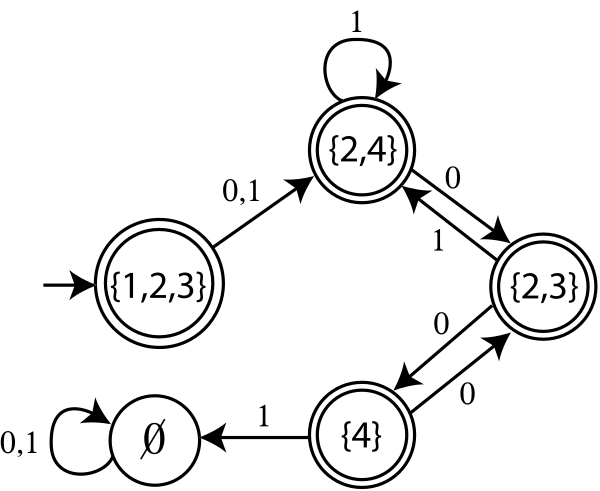
이렇게 생겼습니다. 이거 그래프처럼 생기지 않았나요? 맞습니다! 그래프입니다.

문자열 알고리즘을 이해하는데 왜 그래프 이론부터 시작하는지 구구절절 설명하기에는 제 역량이 부족하니 대충 설명하면서 빠르게 본질로 다가가겠습니다.

상태기계는 어떤 입력을 받으면 미리 정해진 규칙에 따라 다음 상태로 전이하며 입력을 처리하는 장치를 뜻합니다. 유한상태기계의 설계 및 작동에 대해 궁금하다면 Contact 문제를 풀어보면서 직접 익힐 수 있습니다.

입력의 종류가 두 가지인 예시

지금부터 우리는 정해진 패턴을 최대한 많이 찾는 상태기계를 만들어 볼 겁니다. 하지만 처음부터 너무 복잡한 걸 목표로 잡으면 제대로 따라가기 힘드니까, 가장 단순한 것에서부터 시작하겠습니다.

• 입력은 \(0\) 또는 \(1\)로만 이루어져 있다.
• 찾아야 하는 패턴은 무조건 \(1\)과 \(0\)이 번갈아 나오는 패턴이다.

IOIOI 문제는 사실 KMP 알고리즘을 몰라도 풀 수 있을 정도로 쉽습니다. KMP 정도의 문자열 알고리즘이 궁금해서 이 글을 읽고 있는 수준이라면 아마 오래전에 풀어보셨을 겁니다. 혹시 풀지 않았어도 괜찮습니다. 이 글을 마저 읽기 전에 풀어보세요.

대부분의 코드는 간단한 아이디어를 캐치하여 답을 구하고 있습니다. 패턴을 모두 찾은 후에도 문자를 2개씩 끊어 OI가 반복되는 개수를 구하면 빠르게 패턴을 완성할 수 있습니다. 그런데, 2개씩 끊는다는 것은 생각보다 심오한 의미를 담고 있습니다.

이제 예시를 상태기계로 접근해봅시다.

우선 단순히 패턴을 찾는 그래프를 만들겠습니다.

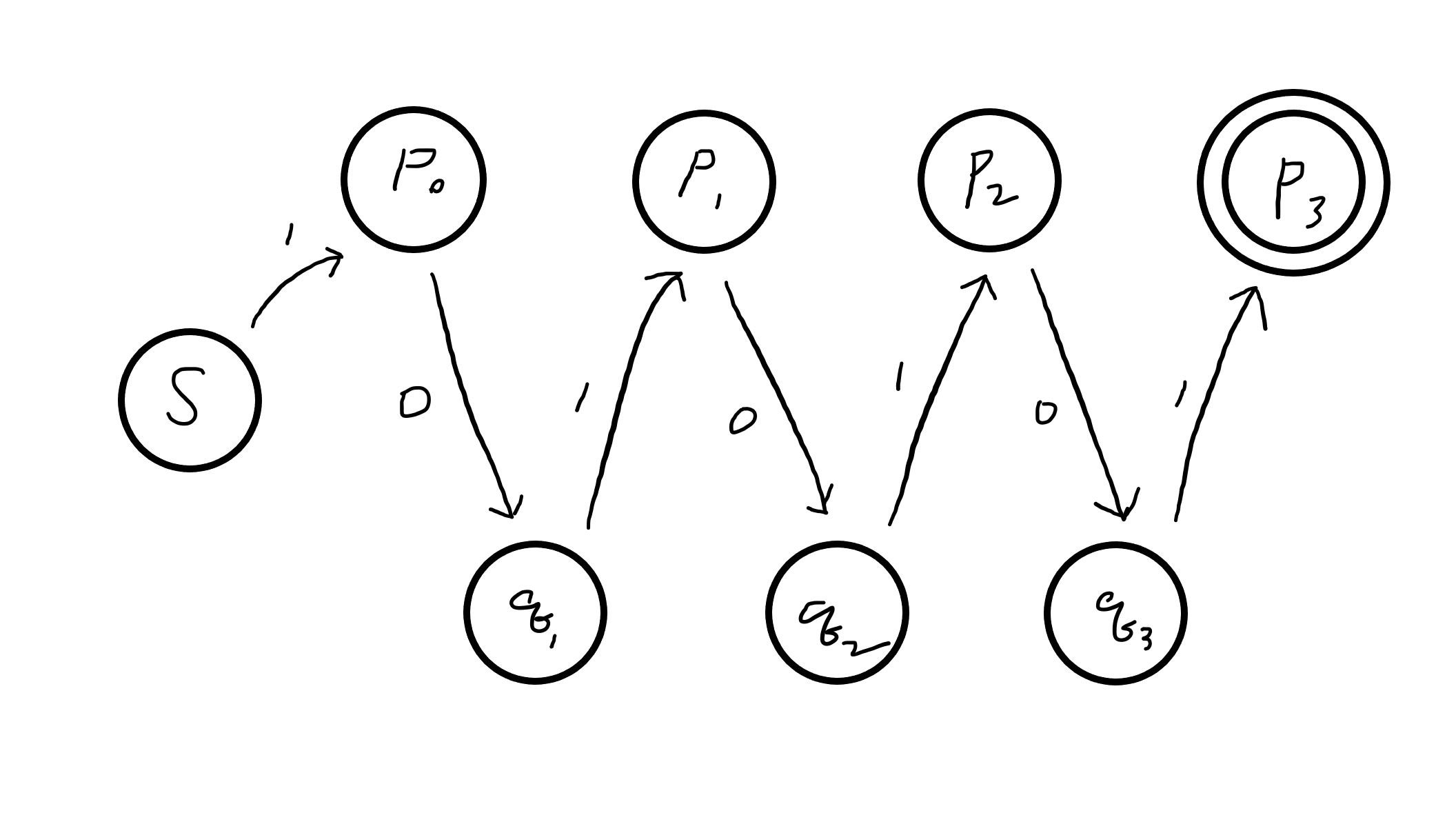
• 원은 그래프의 정점입니다.
• 각 정점은 방향 있는 간선으로 연결됩니다.
• 각 간선은 정해진 입력이 있어서, 어떤 상태에서 입력을 받으면 다음 상태로 전이됩니다.

유한상태기계는 정해진 개수의 상태를 갖고, 규칙에 따라 다음 상태로 넘어가면서 입력을 처리합니다. 위 그래프는 1, 0, 1, 0, … 처럼 번갈아 들어오는 입력에 대해 다음 상태로 넘어가면서 \(P_N\)을 찾아냅니다. 이 문제를 푼 대부분의 사람들은 현재 문자가 I일 때는 패턴 매칭을 시작하고, O일 때는 뛰어넘는 코드를 작성합니다. 사작 상태에서 0일 때는 더 진행할 수 없다는 뜻으로 해석할 수 있습니다.

그런데 안타깝게도 위 그래프에서 처음 O일 때는 화살표가 없습니다. 그 뿐만이 아닙니다. 지금 상태의 그래프는 완성되어 있지 않습니다. 문자가 반복되는 경우(00, 11)를 처리하지 못하고 있습니다.

실패 처리

유한상태기계가 입력 처리를 중단하지 않도록 하려면 각 정점에서는 주어질 수 있는 모든 입력에 대해 전이될 수 있는 다음 상태가 있어야만 합니다. 각 정점에서 두 개의 화살표가 나가고 있어야 한다는 뜻입니다. 마저 채워봅시다.

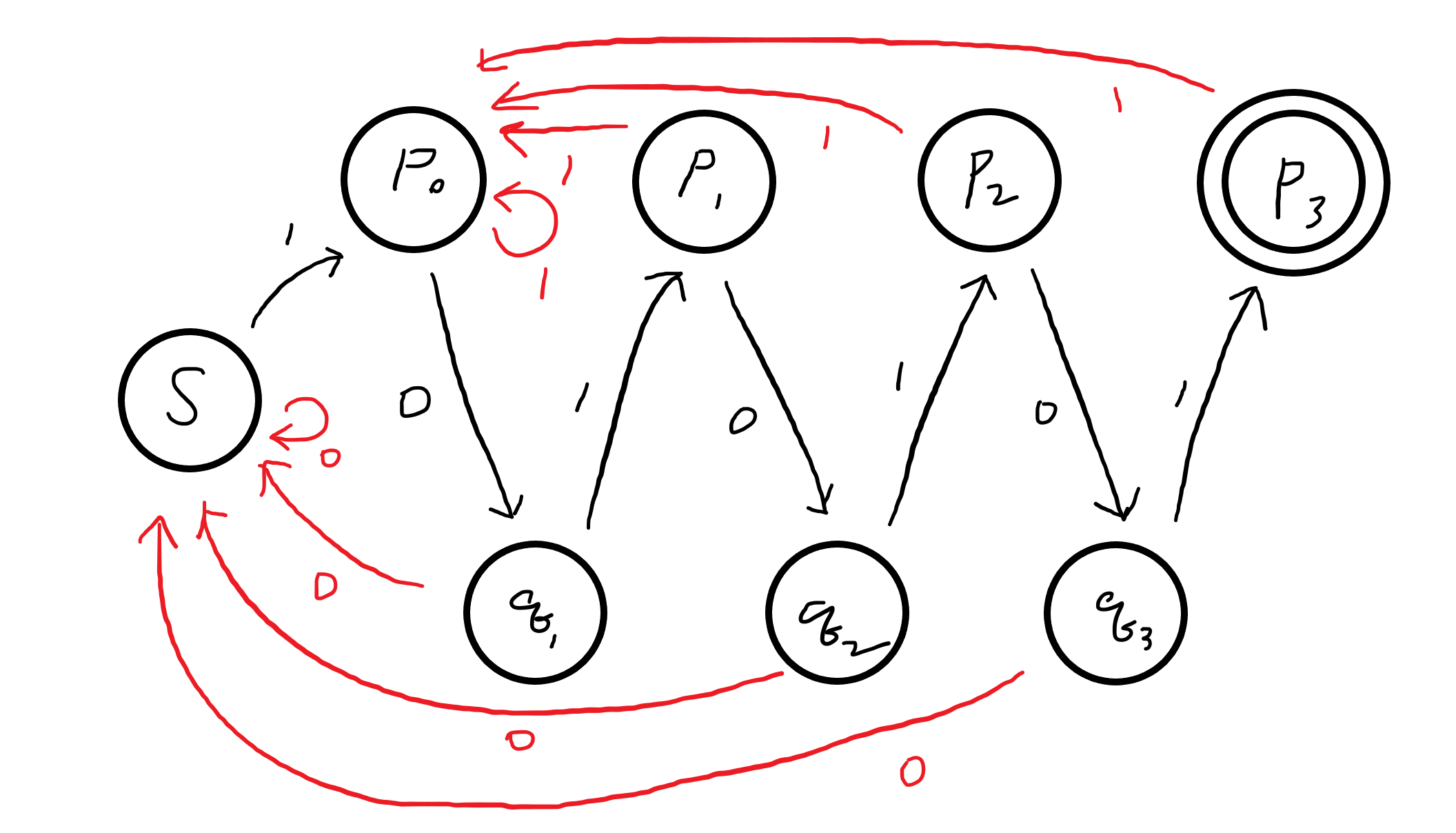
1을 입력받아야 할 상황에서 0을 받을 경우엔 처음으로 돌아갑니다. 0을 입력받아야 할 상황에서 1을 받았다면, 어찌저찌 패턴으로 써먹을 문자가 하나 있긴 하니까 두 번째 상태로 돌아갑니다.

이제 간선이 하나 남았습니다. 그런데 마지막 상태에서 0을 받으면 어디로 가야 할까요?

잠시 고민해보시면 좋습니다.

정답은 바로 이전 상태로 돌아가는 것입니다.

우리의 목표는 패턴을 최대한 많이 찾는 것입니다. 이미 찾은 패턴에서 가능한 많은 부분을 다음 패턴으로 이어나가고 싶습니다. IOIOIOI의 뒷부분에는 이미 IOIOI가 있고, 그 상태에서 O를 받으면 IOIOIO를 만들 수 있습니다.

하지만 지금 상태로는 좀 알아보기가 힘드니까 그래프를 조금 다르게 그리겠습니다.

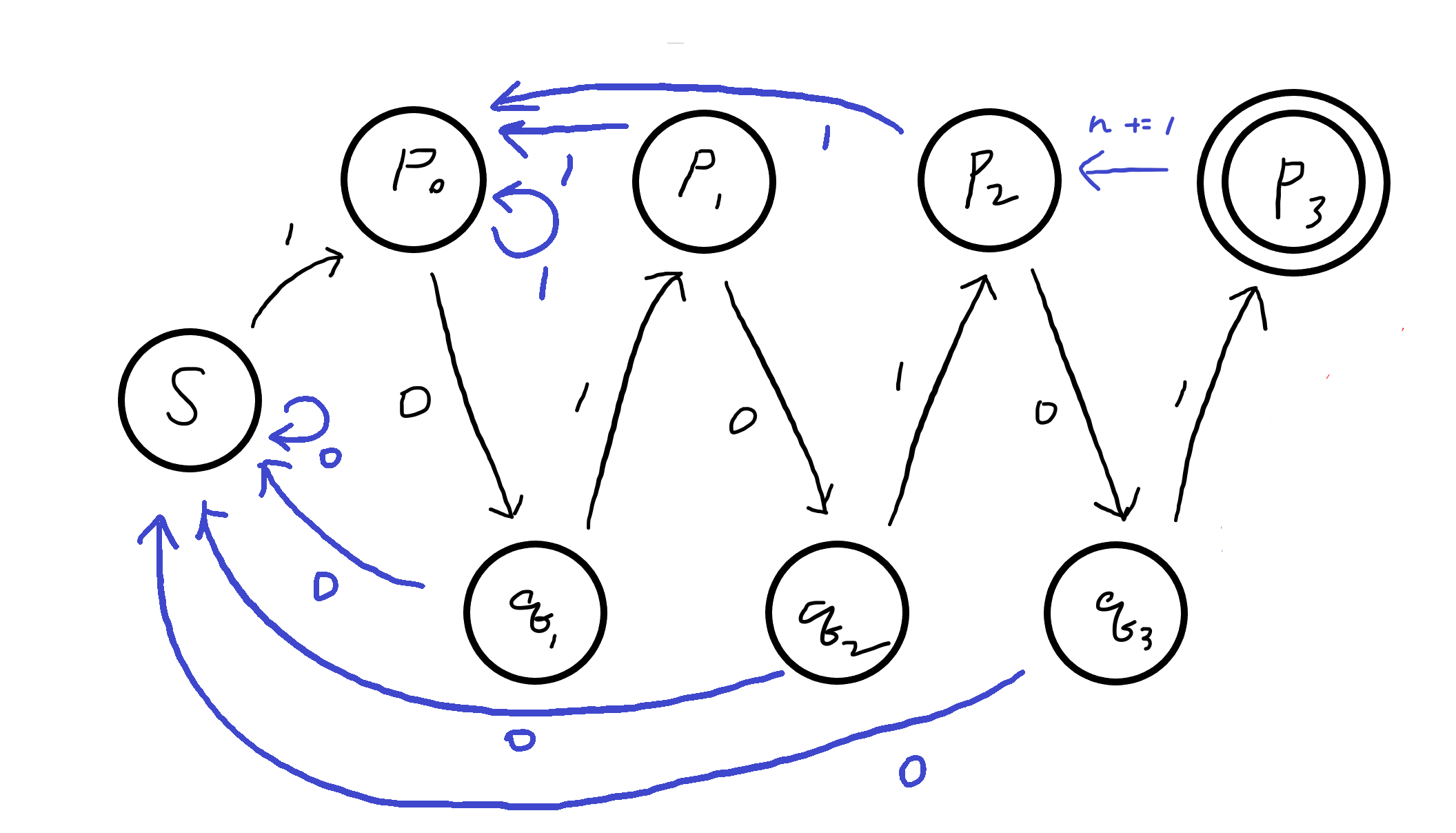
IOIOIOI 패턴을 찾는데 성공했다면 개수를 1 증가시킨 후, IOIOI를 찾은 상태로 돌아갑니다. 왜 OI만 찾아도 패턴이 빠르게 찾아지는지 조금은 알 것 같습니다.

이제 완성된 상태기계로 문제를 해결할 수 있습니다. 여기서 집중해서 봐야 하는 부분은, 파란 간선이 어디로 돌아가고 있는가입니다. 시작 정점부터 0, 1, …, 7로 번호를 부여할 경우 다음 수열이 됩니다.

• 0, 1, 0, 1, 0, 1, 0, 5

이 수열은, KMP 알고리즘에서 IOIOIOI를 찾기 위한 fail함수입니다.

KMP

이제 입력으로는 모든 알파벳이 들어올 수 있습니다. 다음 패턴을 찾는 상태기계를 만들고 싶습니다.

고구마호박호박고구마호구마호박고구마

• 고구마호박?
• 호박고구마.
• 호구마?
• 호박고구마!

우선 단순히 진행하는 그래프를 만듭니다.

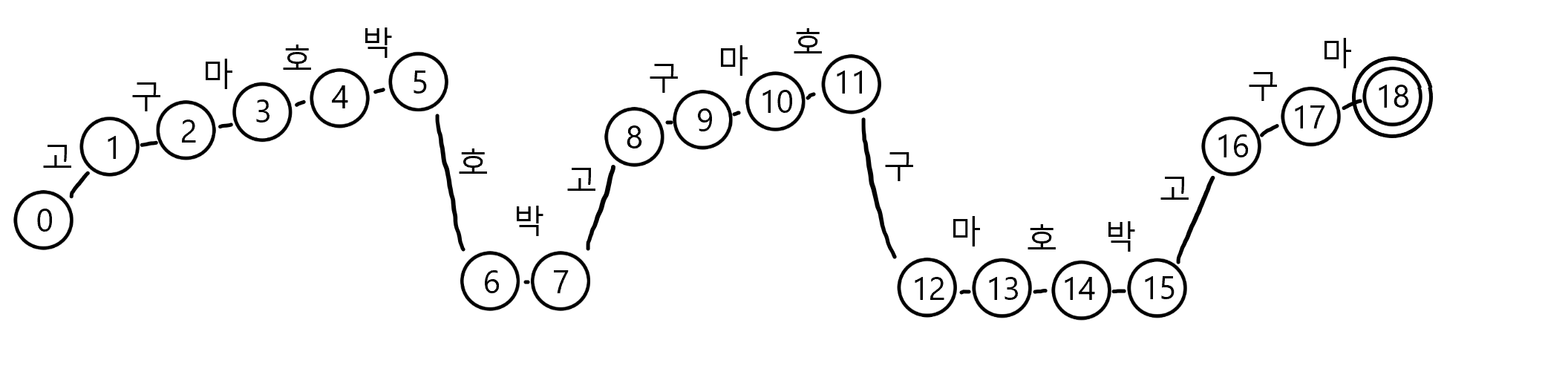
각 간선에 대해 다음 상태로 진행할 수 있는 입력은 딱 한 개씩입니다. 나머지 다른 입력에 대해서는 다음 전략을 취할 수 있습니다.

• 현재까지 찾은 패턴에서 쓸만한 뒷부분은 챙긴다.
• 챙긴 뒷부분의 길이만큼은 이미 찾은 상태나 마찬가지다!
• 그럼 그 때로 돌아가서 입력을 다시 확인한다.
• 다음 상태로 진행할 수 있다면 넘어간다!
• 아니라면 현재까지 찾은 패턴에서 쓸만한 뒷부분은 챙긴다…

고구마호박호구마를 읽는다고 합시다.

다음 상태로 넘어갈 수가 없습니다. 챙길 수 있는 것도 없네요. 처음 상태로 돌아갔지만 여전히 넘어갈 수가 없습니다. 그럼 그냥 다음 문자를 읽습니다.

고구마호박호박고구마호박...을 읽는다고 해봅시다.

안타깝게도 다음 상태로 넘어가기 위해서는 입력이 구여야만 합니다. 그럼 지금까지 찾은 패턴에서 쓸만한 뒷부분을 챙기고, 그만큼 뒤로 돌아갑니다.

이걸 코드로 쓰면 다음처럼 됩니다.

std::vector<int> kmp(const std::string& T, const std::string& P) {
    std::vector<int> result;
    std::vector<int> pi = getPi(P);
    
    int t = T.length(), p = P.length(), j = 0;
    
    for (int i = 0; i < t; ++i) {
		// j > 0: 0번 상태에선 더 이상 뒤로 돌아갈 곳이 없습니다!
		// T[i] != P[j]: 다음 상태로 넘어가는 입력이 현재 입력과 다를 때까지
        while (j > 0 && T[i] != P[j])
			j = pi[j - 1]; // 상태를 뒤로 돌립니다
        if (T[i] == P[j]) { // 다음 상태로 전이 가능하다면
            if (j == p - 1) { // 패턴을 완성했다면
                result.push_back(i - p + 1); // 위치 추가
                j = pi[j]; // 챙길 수 있는 만큼 챙겨서 뒤로 돌아갑니다
            }
            else ++j; // 다음 상태로 전이
        }
    }
    return result;
}

문자열을 읽어들이는 상태기계로 KMP를 설명하는 것은 나중에 아호-코라식과 같은 알고리즘으로 이해를 확장하는 데도 도움이 됩니다.