백준 12670 - The Year of Code Jam
이제 SSAFY도 끝나가고, 딱히 좋은 소식 없이 방구석에서 공부만 하고 있습니다. 이번에 풀어본 문제는 최대 유량을 어떻게 적용해야 하는지 그 발상을 떠올리는 게 까다로운 The Year of Code Jam입니다.
\(N\)월은 각각 \(M\)일씩 있습니다. 달력에 대회 참가일을 파란 색으로 칠할 때, 인접한 칸의 수에 따라 \(4 - k\)만큼의 점수를 매깁니다. ? 칸에 파란색을 칠할지 선택할 수 있을 때 최대 점수를 만들면 됩니다.
사실 문제 설명만 읽어서는 이게 그래프 문제인지도 잘 감이 안 잡힐 수 있습니다. 물론 백준 1페이지 문제 중 하나인 컨닝을 풀어봤기 때문에 적어도 비슷한 방향으로 접근해볼 수는 있었습니다.
우선 격자에서 인접한 4개의 칸에 간선을 잇고, 거기에 어떤 식으로든 유량을 흘려서 최대값을 구한다. 언뜻 생각해보면 그럴듯하지만 막상 간선을 아무렇게나 잇는다고 해서 원하는 값이 나와주지 않습니다. 어떻게 간선을 연결할지, 애초에 어떤 컷을 구할지도 모르고서는 제대로 풀 수가 없습니다.
가장 먼저 문제를 단순하게 만들어봅시다. 인접한 칸을 간선으로 연결한 그래프에서, 무엇이 구하고자 하는 값이 될까요? 인접한 . 칸과 # 칸 사이에만 간선을 남길 때, 그 남은 간선의 개수가 바로 점수가 됩니다. 단, 가장자리에 있는 # 칸은 점수가 덜 계산될 수 있으므로 테두리를 추가해줍니다.

체스판처럼 배치되었을 때, 연결된 모든 간선으로는 1의 유량이 흐르고 그것이 발생 가능한 최대 유량이 됩니다. ?를 적당히 . 이나 #으로 바꿔 간선을 남기는 것은, 거꾸로 보면 삭제될 간선을 최소화하는 것이 됩니다. 최소 컷이죠. 그런데 과연 어디서 흘려서 어디로 모이게 해야 할까요. 체스판 말이 나왔으니 문제를 한 번 더 바꿔보겠습니다. \(i\)행 \(j\)열의 . 칸은 인접한 .과는 연결되어 유량이 흐르게 하고, #칸과는 흐르는 것이 없어야 합니다. 그 반대도 마찬가지입니다. 마치 체스판의 흑백 칸이 번갈아 있는 것처럼, \(i + j\)가 짝수인 칸과 홀수인 칸을 나눠 생각해봅시다. 그리고 다음과 같이 판을 바꿔줍니다.
- \(i + j\) 가 홀수일 때,
.는 \(1\),#는 \(2\) - \(i + j\) 가 짝수일 때,
.는 \(2\),#는 \(1\) ?는 \(3\)
인접한 \(1\)과 \(2\)인 정점끼리만 간선을 연결한다고 할 때, \(3\)인 정점을 제외하고는 이분 그래프가 만들어집니다. 그리고 \(3\)인 정점을 적당히 옮겨준다면…
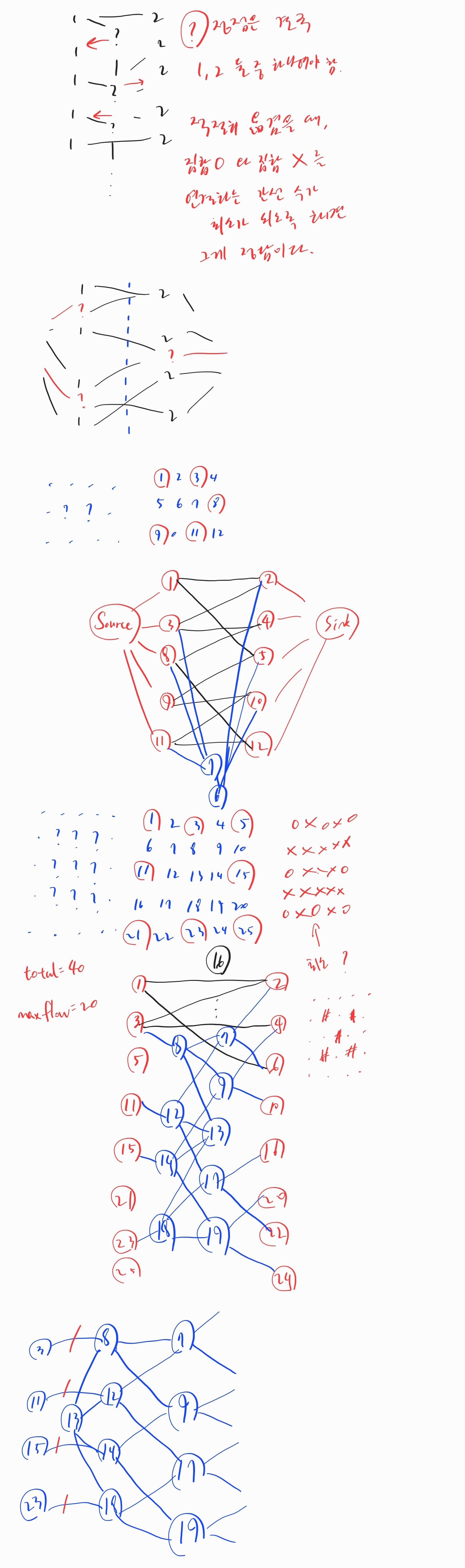
결국 3인 정점들을 적당히 옮겨서 연결된 간선 수가 가장 적은 이분 그래프를 만드는 문제가 됩니다. \(1\) 정점들로부터 \(2\) 정점으로 유량을 흘리면 최소 컷을 구할 수 있습니다.
#include <iostream>
#include <vector>
#include <queue>
#include <map>
const int MAX = 3000;
const int INF = 1e9;
const int source = MAX - 2;
const int sink = MAX - 1;
int T, N, M;
char S[51];
int map[52][52];
std::map<int, int> c[MAX], f[MAX];
int work[MAX], level[MAX];
std::vector<int> A[MAX];
int dx[4] = { -1, 1, 0, 0 }, dy[4] = { 0, 0, -1, 1 };
bool bfs(int S, int T) {
std::fill(level, level + MAX, -1);
level[S] = 0;
std::queue<int> q;
q.push(S);
while (!q.empty()) {
int v = q.front(); q.pop();
for (const int& u : A[v]) {
if (!~level[u] && c[v][u] - f[v][u] > 0) {
level[u] = level[v] + 1;
q.push(u);
}
}
}
return ~level[T];
}
int dfs(int here, int target, int flow) {
if (here == target) return flow;
for (int& i = work[here]; i < A[here].size(); ++i) {
int next = A[here][i];
if (level[next] == level[here] + 1 && c[here][next] - f[here][next] > 0) {
int ret = dfs(next, target, std::min(c[here][next] - f[here][next], flow));
if (ret > 0) {
f[here][next] += ret;
f[next][here] -= ret;
return ret;
}
}
}
return 0;
}
int dinic(int S, int T) {
int totalFlow = 0;
while (bfs(S, T)) {
std::fill(work, work + MAX, 0);
while (1) {
int flow = dfs(S, T, INF);
if (flow == 0)
break;
totalFlow += flow;
}
}
return totalFlow;
}
int solve() {
for (int i = 0; i < MAX; ++i) {
c[i].clear();
f[i].clear();
A[i].clear();
}
std::cin >> N >> M;
for (int i = 0; i <= N + 1; ++i)
for (int j = 0; j <= M + 1; ++j)
map[i][j] = 1 << ((i ^ j) & 1);
for (int i = 0; i < N; ++i) {
std::cin >> S;
for (int j = 0; j < M; ++j) {
if (S[j] == '#') map[i + 1][j + 1] = 1 << (~(i ^ j) & 1);
if (S[j] == '?') map[i + 1][j + 1] = 3;
}
}
for (int i = 0; i <= N + 1; ++i) {
for (int j = 0; j <= M + 1; ++j) {
int node = i * (M + 2) + j;
if (map[i][j] == 1) {
A[source].push_back(node);
c[source][node] = 4;
f[source][node] = 0;
}
if (map[i][j] == 2) {
A[node].push_back(sink);
c[node][sink] = INF;
f[node][sink] = 0;
}
for (int d = 0; d < 4; ++d) {
int di = i + dx[d], dj = j + dy[d];
int dn = (M + 2) * dx[d] + dy[d];
if (di < 0 || di > N + 1 || dj < 0 || dj > M + 1) continue;
A[node].push_back(node + dn);
c[node][node + dn] = 1;
f[node][node + dn] = 0;
}
}
}
int total = 2 * N * M + 3 * M + 3 * N + 4;
int max_flow = dinic(source, sink);
return total - max_flow;
}