분수 objective function 최대화

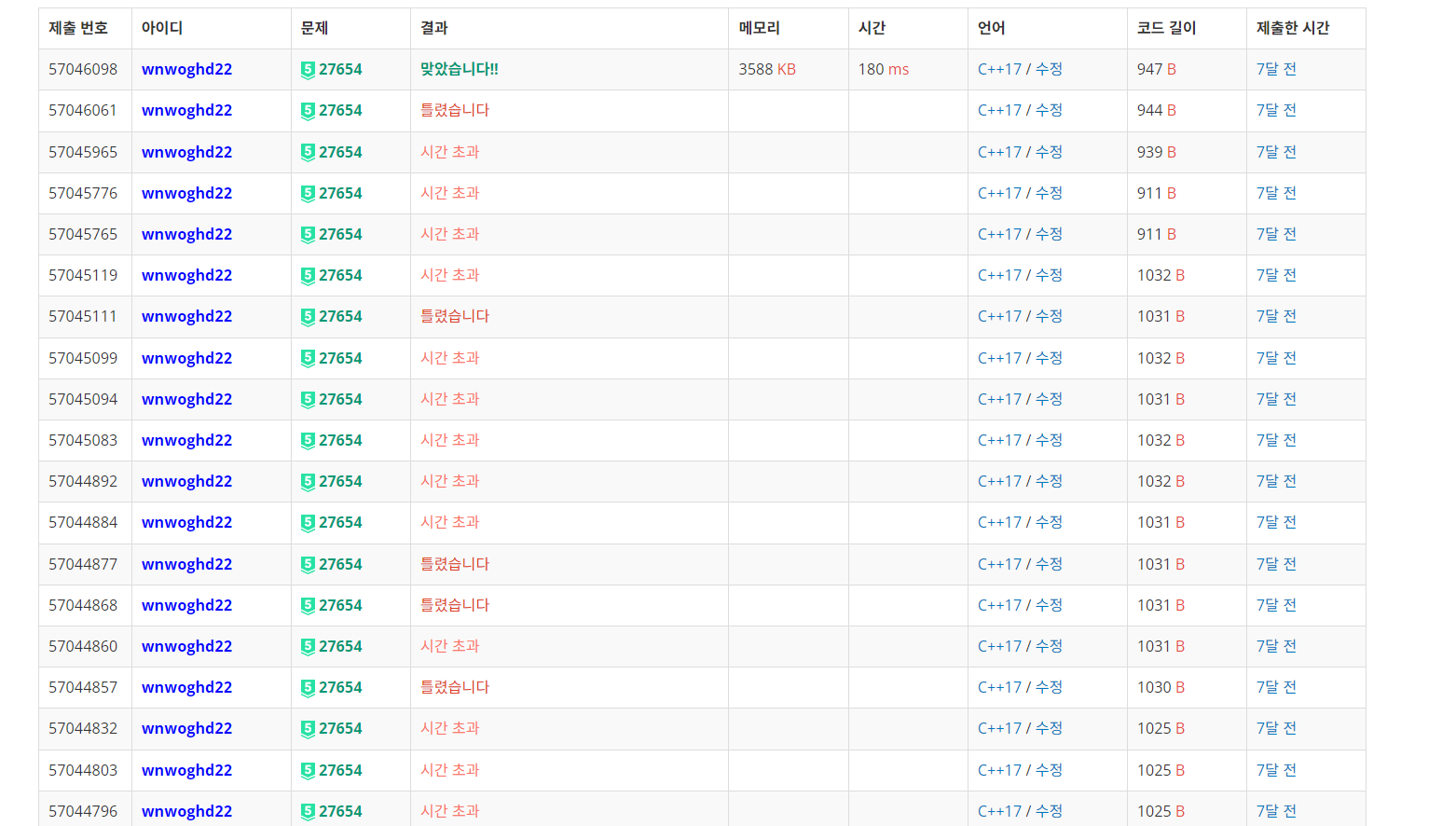
가끔 PS 문제들을 보면 분수 가중치 합이 최대가 되는 부분집합을 찾는 것들이 나옵니다. 마냥 많이 선택하는 것도 답은 아니고, 그렇다고 가중치가 큰 것들을 선택해가는 것만도 답은 아닌 경우가 더러 있습니다. 시험 문제가 그런 유형인데요.

\[\sum P_x \over \sum Q_x\]

K개의 분수를 골라 분모와 분자를 각각 더한다고 할 때, 위 식을 최대화하면 됩니다. 단, 각 \(P_i\)에 대해 \(Q_i\) 값은 고정되어 있습니다. 이게 마냥 쉬운 것은 아닌 게, 그리디하게 분수 값이 큰 순서대로 골라 더한다고 해서 항상 최적이 되지 않기 때문입니다. 그렇다고 모든 경우의 수를 다 고려해버린다면 그건 다항 시간 내에 해결이 불가능해집니다. 이런 유형의 문제는 식을 약간 변형시키면 결정문제로 치환할 수 있습니다.

\[{\sum P_x \over \sum Q_x} \ge k\]

로 식을 만들면, 이제 왼쪽 항이 \(k\)보다 큰 경우가 있는지 없는지를 판단하는 결정문제가 됩니다. 식을 좀 더 고쳐보면…

\[\sum P_x \ge k \sum Q_x\] \[\sum P_x - k \sum Q_x \ge 0\]

이제 왼쪽 식이 0보다 크거나 같다면, 분수를 적절히 골라 \(k\) 이상의 값을 얻을 수 있음을 알 수 있습니다. 그리고 식을 저렇게 바꾸면 좋은 게 하나 더 있는데, 이젠 자명하게 그리디한 방식으로 \(P_i - k Q_i\)가 큰 순서대로 골라 더하면 답이 나온다는 것입니다!

이 개념을 제대로 이해하고 구현하는 데 꽤 애를 먹었습니다.

struggle

54번 시도 끝에 맞혔습니다…

비슷한 문제 유형은 더 많은데, AtCoder 문제도 하나 보도록 하겠습니다.

임의의 DAG가 있어서 모든 간선은 항상 \(i\)에서 \(j\)로만 간다고 합시다.(단, \(i \lt j\)) 그리고 각 간선에는 분수 가중치가 있습니다. 이제 \(1\)부터 \(N\)까지 이동할 때, 분수 가중치 합이 가장 크게 만들면 됩니다.

첫 번째 문제가 매개 변수 탐색과 그리디였다면, 이번 문제는 DP로 판별식을 세워야 합니다. 젓 번째와 마찬가지로 이번 문제도 DP만 적용해서는 제대로 된 답을 얻기가 힘듭니다.

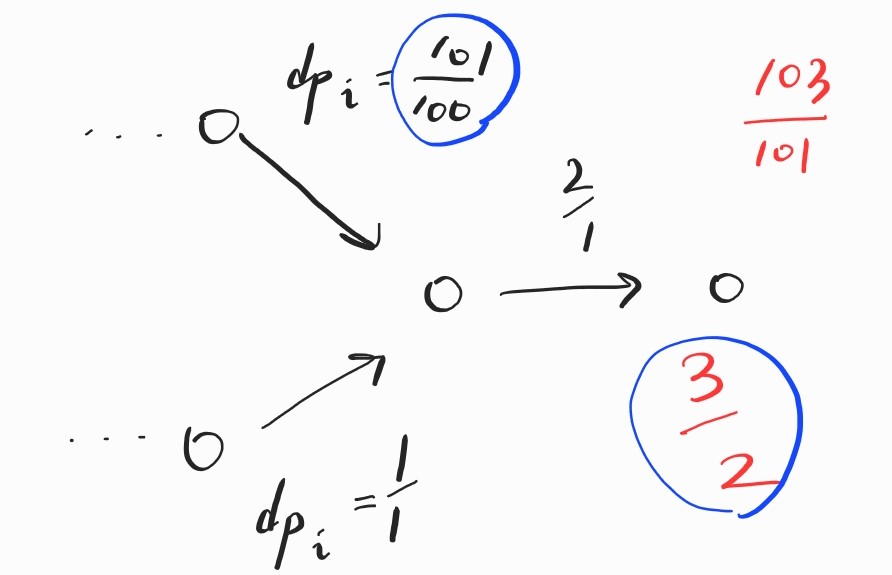
example

전략은 DP더라도, 매 순간의 점화식은 그리디함이 보장되어야 최종적으로는 최적해를 얻을 수 있습니다. 하지만 위 그림의 예시는 전혀 그러질 못하고 있습니다. DP는 결국 매 순간 가장 큰 하나만을 취해나가지 않고서는 의미가 없으므로, 이번에도 식을 위 문제처럼 변형시켜야만 합니다.

typedef long double ld;
const ld TOL = 1e-12;
const int LEN = 2e5 + 1;
const ld INF = 1e17;

struct Edge {
	int u, b, c;
};

int N, M;
std::vector<Edge> g[LEN];
ld dp[LEN];

ld f(ld x) {
	dp[1] = 0;
	for (int i = 2; i <= N; ++i) dp[i] = -INF;
	for (int v = 2; v <= N; ++v) {
		for (const Edge& e : g[v]) {
			ld val = e.b - x * e.c;
			dp[v] = std::max(dp[v], dp[e.u] + val);
		}
	}
	return dp[N];
}

ld bs() {
	ld l = -INF, r = INF, m;
	ld result = -INF;
	while (r - l > TOL) {
		m = (l + r) / 2;
		if (f(m) > -TOL) {
			result = std::max(result, m);
			l = m + TOL;
		}
		else r = m - TOL;
	}
	return result;
}

이건 그래도 저번 문제를 풀면서 흘린 눈물의 양만큼 빨리 풀 수 있었던 것 같네요.

이러한 유형의 문제를 몇 개 더 골랐습니다.

팀의 난이도 (매우 어려움)

GC-비율

PROSJEK

Categories