삼성 역량평가 B형 시험 때 써먹을 수 있을까 싶어 스플레이 트리를 공부하고 있는 요즘입니다… 이번엔 좀 어려운 문제를 풀어봤습니다. 바로 불순 분자 만들기인데요, 옛날 대회 때 문제인 것 같습니다. 참가자는 20명 남짓이었던 걸로 보이고, 어딜 봐도 에디토리얼을 찾을 수가 없었습니다. 세그먼트 트리와 HLD를 접하고 나서 꼭 풀어보고 싶은 문제였는데, 며칠 고민한 끝에 답이 보였습니다.

문제에서 구하고자 하는 것은 다음과 같습니다.

트리 위의 두 점 간을 최단 경로로 이동하는 궤적들이 존재한다.
정해진 두 점 간의 최단 경로 상에, 그 궤적들이 몇 개 존재하는가?

트리 상에서의 궤적, 구간 쿼리 등등 언뜻 봐도 세그먼트 트리와 HLD의 냄새가 납니다. 사실 출제 후기를 봐서는 이 문제가 그리 단순한 의도로 만들어진 건 아니더군요. 어쨌든 더 쉽고(마냥 쉽진 않습니다.) 단순한(사실 꽤 복잡합니다.) 풀이가 있으면 그쪽으로 가는게 맞죠.

일단 넓은 구간 쿼리와 누적합 등등의 요소가 나온다는 건 알겠습니다. 그래서, 궤적은 어떻게 표현되는 것이 좋을까요?

정점 가중치

우선, 궤적을 지나갈 때마다 방문하는 정점들에 1씩 값을 누적해가는 것을 생각해볼 수 있습니다.

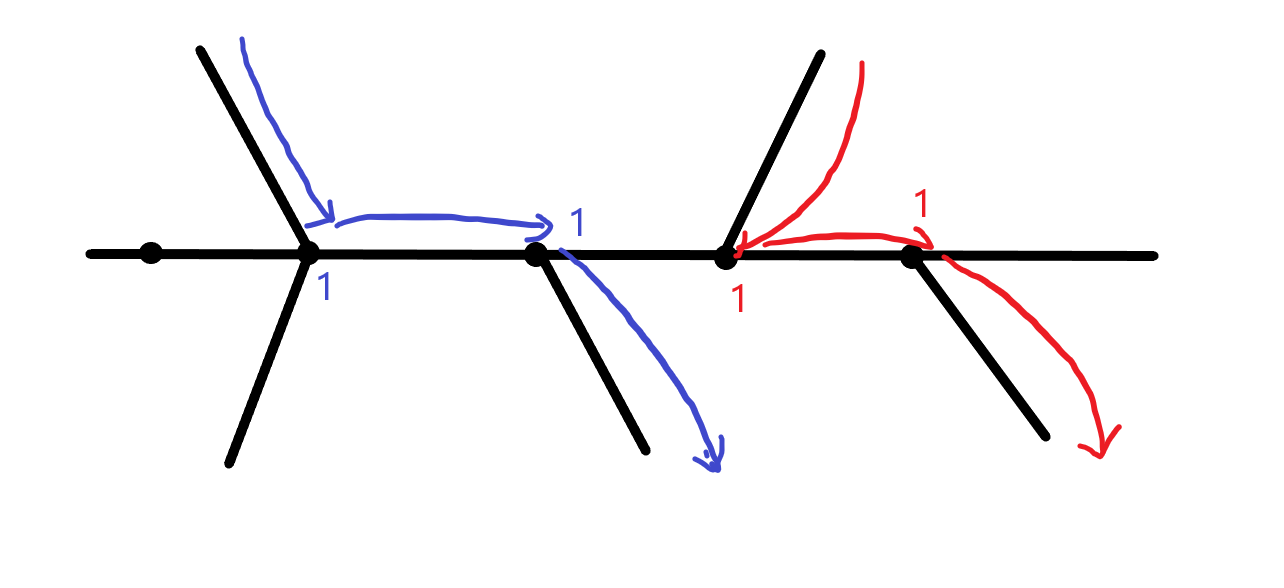
weight-vertex-only

하지만 누적된 값들을 보면서, 우리는 무엇을 알 수 있을까요? 경로 상의 최대값이 궤적의 수가 되지는 않습니다. 위 그림만 보더라도, 가로로 늘어선 경로 상의 최대값은 1이지만, 궤적의 수는 파란색과 빨간색 두 개지요. 최대값이 아닌 누적합이라면 어떻게 될까요? 하지만 그것도 답이 되진 않습니다. 파란 경로가 3개의 정점을 방문하면 누적합은 3이지만, 궤적의 수는 한 개 뿐입니다.

간선 가중치

이번엔 간선에 가중치를 부여해보죠.

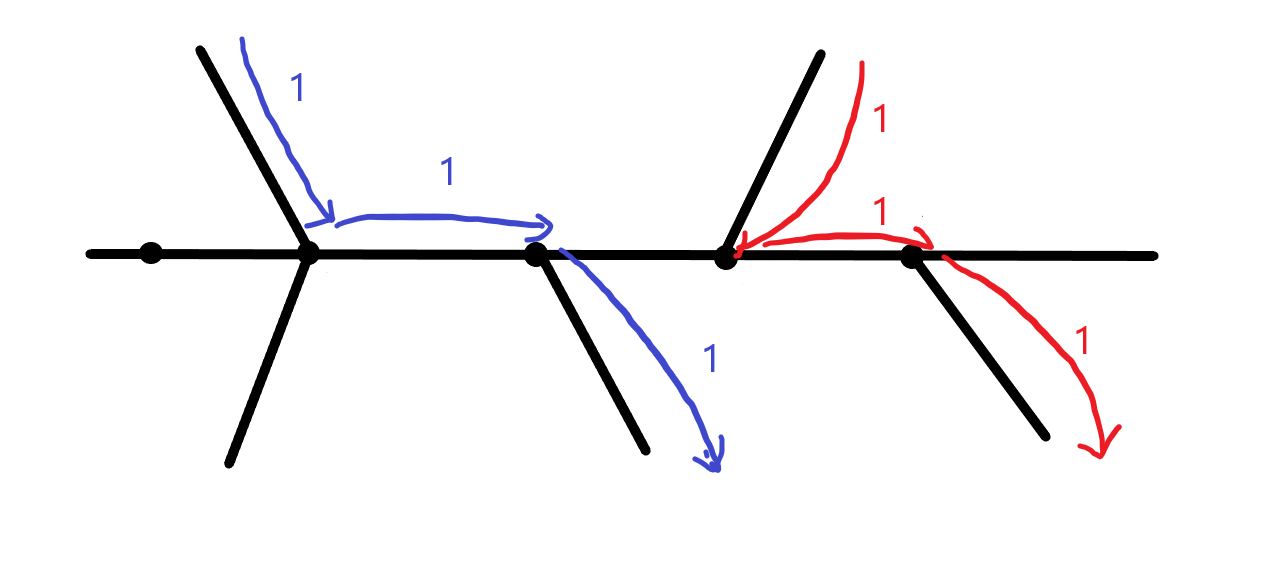
weight-edge-only

이번에도 마찬가지로, 단순히 간선에 누적되는 값들만 보고는 아무것도 알 수 없습니다. 위에서와 마찬가지로, 최대값이나 누적합 등으로는 궤적의 수를 알아낼 방법이 없습니다.

정점도 간선도 아니라면, 희망은 없는 걸까요?

둘 다 써본다

그럼 이렇게 해보죠. 궤적이 지나갈 때마다, 정점과 간선 모두에 가중치를 부여합니다.

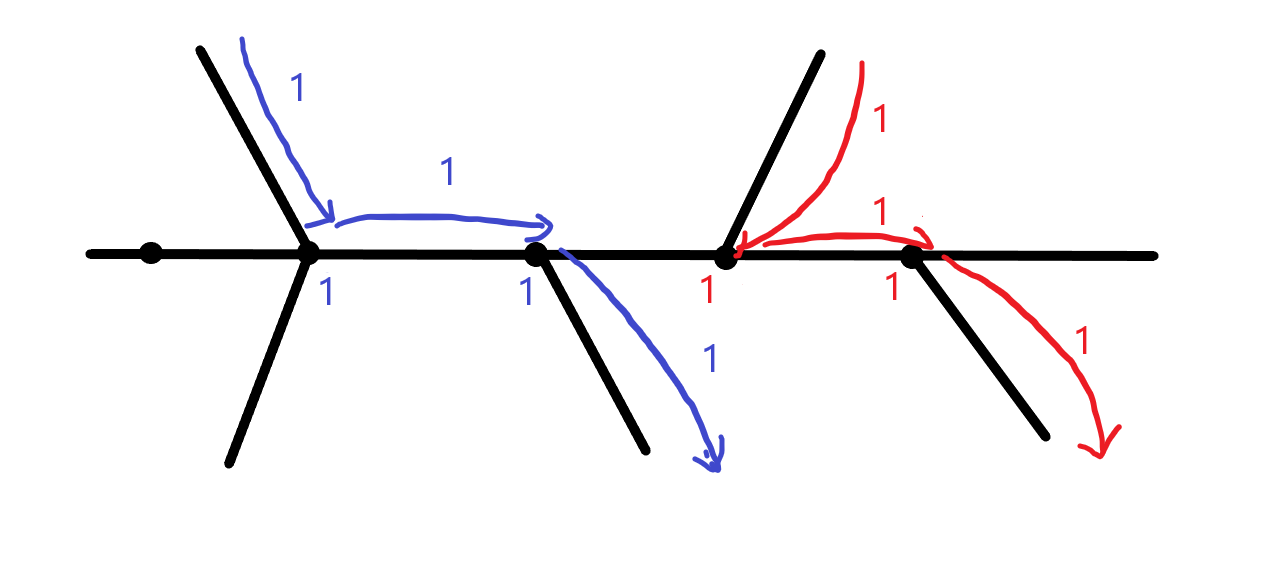
weight-both

이러면 뭔가 달라질까요?

이렇게 생각해볼 수 있습니다. 어떤 간선에 가중치가 부여되어 있다면(\(k\)), 정점들에는 딱 1 더 큰 가중치가 부여될 수 밖에 없습니다(\(k+1\)). 경로 상 모든 정점들의 가중치들을 다 더한 후, 모든 간선의 가중치는 다 빼주면 한 점에서 출발하는 궤적들의 수만큼만 남게 됩니다.

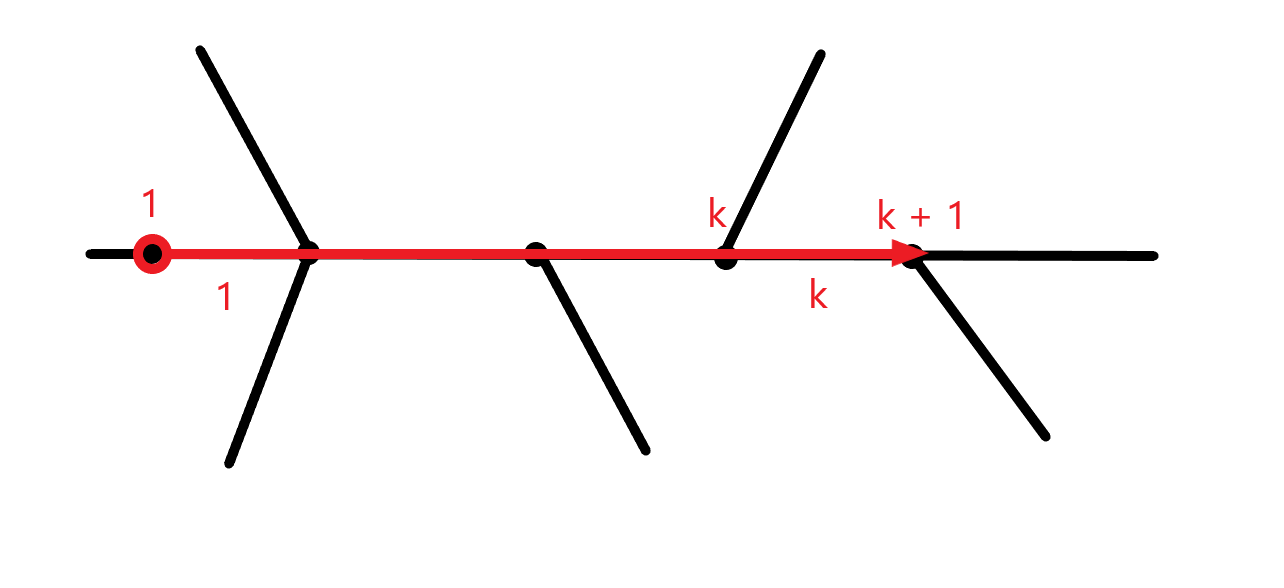
weight

일반성을 잃지 않고, 경로 상에서만 궤적의 시점과 종점이 존재할 때 뿐 아니라 들어가거나 나가는 경우에서도 이 규칙은 관찰되며, 궤적이 몇 개 겹쳐있든 상관없이 일정합니다. 물론 궤적이 정확히 어떻게 생겼는지는 알 수는 없어도, 누적된 값을 빼서 궤적의 수를 구할 수는 있게 되었습니다.

이제 문제는 트리 상에서 세그먼트 트리를 쓰는 것으로 넘어갑니다.

Heavy-light decomposition

이 문제가 직선 상에서 궤적의 수를 세는 것이었다 해도 쉽지는 않았을 겁니다. 더군다나 트리라면, 단순한 방법으로는 구간 쿼리를 빠르게 처리할 수는 없습니다. 이 때 유효한 전략이 트리를 될 수 있는 한 긴 직선들로 쪼개는 겁니다. 이 테크닉에 대해서는 잘 정리해놓은 글들이 많으니 여기선 길게 다루지 않겠습니다.

raw-tree

날 것 그대로의 트리에선 세그먼트 트리를 쓸 여지가 없습니다. 하지만 각 트리의 경로들을 겹치지 않게 잘 쪼개서 \(\log N\)개 정도로 만들면, \(O(\log^2 N)\)으로 구간 쿼리를 처리할 수 있게 됩니다. 그리고 이것이 HLD의 기본 아이디어입니다.

hld

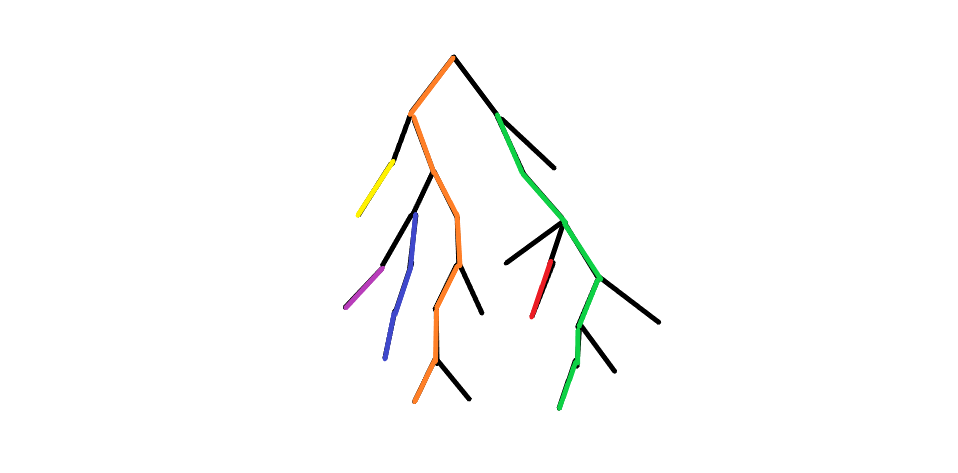
같은 색깔로 묶인 것을 체인이라 할 때, 체인의 수는 \(log N\)개이고, 각 체인에 대한 세그먼트 트리 업데이트를 하면 구간 쿼리를 처리할 수 있으므로 \(O(\log^2 N)\) 정도로 해결이 가능합니다. 실제 구현을 할 때는 양 끝 점이 같은 체인에 속할 때까지 각각 쿼리를 날리면서 체인을 타고 올라갑니다. 결국 LCA에서 만나거나 같은 체인에 속하게 되는데, 이렇게 되면 쿼리가 완성됩니다.

실제 구현은 다음과 같습니다. 제출할 때는 구현 실수 및 잘못된 쿼리 범위 때문에 10번 넘게 삽질을 하긴 했습니다. 정점 세그먼트 트리와는 달리, 간선 세그먼트 트리는 범위 설정이 꽤 까다롭거든요. 각 간선에 부여되는 번호가, 특정 정점에서 그 부모 정점으로 올라갈 때의 그 자식 정점을 따라간다고 합시다. 이 때, 간선 구간 쿼리는 정점과 같이 처리되어서는 곤란합니다. 마지막에 두 정점이 한 체인에 속하게 되었을 때 정점에서 하는 것처럼 구간 쿼리를 날려버리면 간선 하나가 더 포함됩니다. 반드시 범위를 하나 줄여줘야 합니다.

#include <iostream>
#include <vector>

typedef long long ll;
const int LEN = 100'001;

int N, M, Q, S[LEN], E[LEN];
struct SegTree { // 구간합 누적 세그먼트 트리
	ll tree[LEN * 4];
	ll lazy[LEN * 4];
	void propagate(int s, int e, int i) {
		if (lazy[i]) {
			tree[i] += lazy[i] * (e - s + 1);
			if (s ^ e) {
				lazy[i << 1] += lazy[i];
				lazy[i << 1 | 1] += lazy[i];
			}
			lazy[i] = 0;
		}
	}
	void update(int l, int r, ll d, int s = 1, int e = N, int i = 1) {
		propagate(s, e, i);
		if (e < l || r < s) return;
		if (l <= s && e <= r) {
			tree[i] += d * (e - s + 1);
			if (s ^ e) {
				lazy[i << 1] += d;
				lazy[i << 1 | 1] += d;
			}
			return;
		}
		int m = s + e >> 1;
		update(l, r, d, s, m, i << 1);
		update(l, r, d, m + 1, e, i << 1 | 1);
		tree[i] = tree[i << 1] + tree[i << 1 | 1];
	}
	ll get(int l, int r, int s = 1, int e = N, int i = 1) {
		propagate(s, e, i);
		if (e < l || r < s) return 0;
		if (l <= s && e <= r) return tree[i];
		int m = s + e >> 1;
		return get(l, r, s, m, i << 1) + get(l, r, m + 1, e, i << 1 | 1);
	}
} w_edge, w_vert; // 간선, 정점 세그먼트 트리를 각각 만들어주었습니다.

std::vector<int> graph[LEN];
int level[LEN], size[LEN], parent[LEN];
int ord, order[LEN], heavy[LEN];
int ch_ord, chain[LEN], chain_size[LEN], chain_top[LEN];

int dfs(int u, int p = 0) { // 전처리 dfs
	parent[u] = p;
	level[u] = level[p] + 1;
	for (const int& v : graph[u]) {
		if (v == p) continue;
		int sub_size = dfs(v, u);
		if (!heavy[u] || sub_size > size[heavy[u]]) // 크기가 가장 큰 서브트리를 heavy로 삼습니다.
			heavy[u] = v;
		size[u] += sub_size;
	}
	return size[u] += 1;
}
void dfs_euler(int u, int p = 0) { // heavy-light decomposition dfs
	order[u] = ++ord;
	chain[u] = ch_ord;
	if (!chain_size[chain[u]]) chain_top[chain[u]] = u;
	++chain_size[chain[u]];

	if (heavy[u]) dfs_euler(heavy[u], u);
	for (const int& v : graph[u]) {
		if (v == p || v == heavy[u]) continue;
		++ch_ord;
		dfs_euler(v, u);
	}
}

void update(int u, int v) {
	while (chain[u] ^ chain[v]) { // 두 정점이 다른 체인에 속한 동안 반복합니다.
		if (level[chain_top[chain[u]]] > level[chain_top[chain[v]]])
			std::swap(u, v); // 체인이 더 낮은 쪽을 처리해줍니다.
		w_vert.update(order[chain_top[chain[v]]], order[v], 1);
		w_edge.update(order[chain_top[chain[v]]], order[v], 1);
		v = parent[chain_top[chain[v]]]; // 체인 구간 쿼리가 끝났다면 체인의 부모 정점으로 올라갑니다.
	}
	if (level[u] > level[v]) std::swap(u, v);
	if (u ^ v) w_edge.update(order[heavy[u]], order[v], 1); // 간선 구간 쿼리는 범위를 1 줄여야 합니다.
	w_vert.update(order[u], order[v], 1);
}
ll get(int u, int v) {
	ll sum = 0;
	while (chain[u] ^ chain[v]) {
		if (level[chain_top[chain[u]]] > level[chain_top[chain[v]]]) std::swap(u, v);
		sum += w_vert.get(order[chain_top[chain[v]]], order[v]); // 정점 가중치는 더하고
		sum -= w_edge.get(order[chain_top[chain[v]]], order[v]); // 간선 가중치는 뺍니다.
		v = parent[chain_top[chain[v]]];
	}
	if (level[u] > level[v]) std::swap(u, v);
	sum += w_vert.get(order[u], order[v]);
	if (u ^ v) sum -= w_edge.get(order[heavy[u]], order[v]); // IMPORTANT!
	return sum;
}

int main() {
	std::cin >> N >> M >> Q;
	for (int i = 1, u, v; i < N; ++i) {
		std::cin >> u >> v;
		graph[u].push_back(v);
		graph[v].push_back(u);
	}
	dfs(1);
	dfs_euler(1);
	for (int i = 1; i <= M; ++i) std::cin >> S[i] >> E[i];
	for (int i = 0, q, x, y, k; i < Q; ++i) {
		std::cin >> q;
		if (q == 1) {
			std::cin >> x >> y;
			update(x, y);
		}
		if (q == 2) {
			std::cin >> k;
			std::cout << get(S[k], E[k]) << '\n';
		}
	}
}

이 문제는 이렇게 HLD를 쓰는 것 외에도, 원래 출제 의도처럼 센트로이드를 쓰는 것도 있는 것 같고(이쪽은 잘 모르겠습니다.) 단순 오일러 투어 테크닉과 LCA로 푸는 것도 있는 것 같습니다.(이쪽은 머리를 꽤 굴려야 합니다) 아무튼 재미있는 문제였네요.

B형이 따고 싶습니다…

Categories

백준 21730 - 불순 분자 만들기

정점 가중치

간선 가중치

둘 다 써본다

Heavy-light decomposition