백준 1391 - 종이접기
세그먼트 트리를 쓰는 고난도 문제도 좋지만, 좀 더 본질로 돌아가는 것도 나쁘지 않겠죠. 삼성SW역략평가 B형을 준비하면서 좀 더 기본에 충실하기로 했습니다. 그래서 이번에 골라본 문제는 종이접기입니다.
문제 자체는 이해하기 그닥 어려워보일 건 없어보입니다. 숫자가 적힌 종이를 적당히 접어서, 위에서부터 차례대로 숫자가 위치하도록 할 수 있는가 하는 거죠. 자료 크기도 최대 \(2000\)이니까, \(O(N^2)\)으로 풀어도 될 것 같긴 합니다.
사실 이걸 어떻게 접근해야 하나 생각을 꽤 오래 했습니다. 다음의 특성을 알게 되면 이야기가 빨라지죠. 그림을 봅시다.
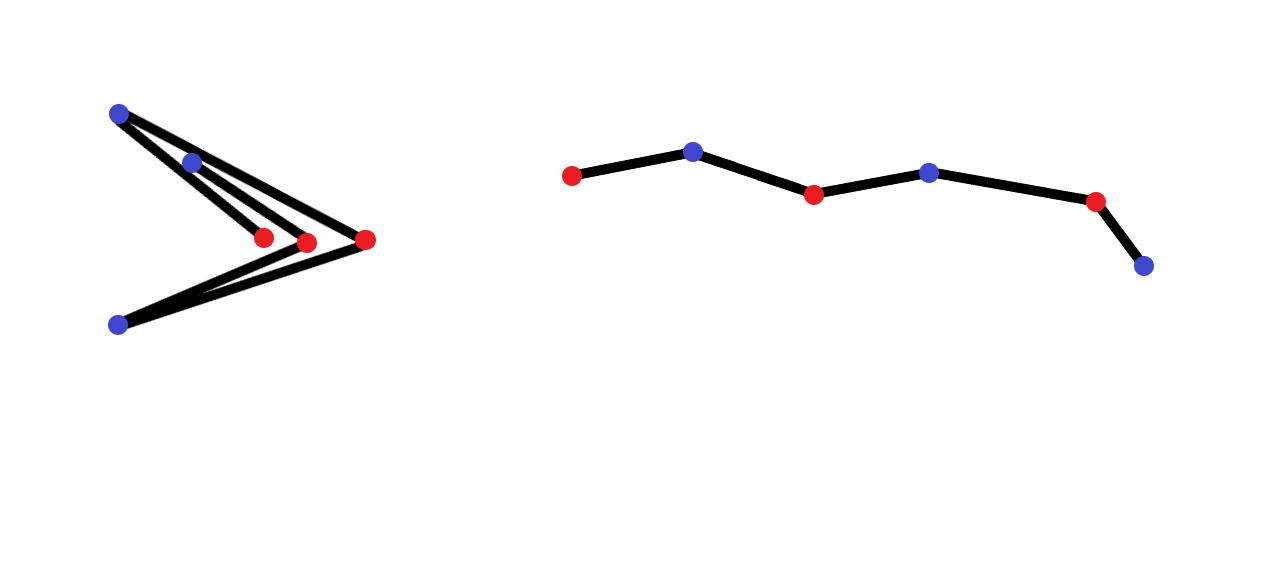
아무렇게나 접어올린 종이의 한쪽 끝에는 빨간 마커로, 반대쪽은 파란 마커로 표시했습니다. 그리고 그 종이를 펴보면 색깔이 번갈아가며 나타납니다. 조금만 깊게 생각해보면 좌우가 번갈아가며 나타난다는 건 쉽게 떠올릴 수 있습니다. 그리고…

문제의 조건을 충족하여 종이를 접었을 때, 좌우는 각각 유효한 괄호문자열이 됩니다. 반대로, 좌우 모두가 유효한 괄호문자열이 아니라면, 문제의 조건을 충족하도록 접을 수 없습니다.
이제 종이의 숫자들이 조건을 충족하는지 판단하기 위해서는 괄호문자열을 두 번 검사하면 된다는 것까진 알았습니다. 또한 문제의 괄호는 단지 몇 종류의 괄호가 아니라, 각각 그 짝이 정해져 있는 특수한 형태의 문자열이긴 합니다. 그런데, 그래서 그 괄호문자열 검사를 어떻게 할까요?
위 그림에서, 빨간 괄호문자열을 판단한다고 해봅시다. 종이에서 인접한 두 숫자간에는 짝지어진 괄호가 생성됩니다. 그 괄호들을 숫자에 적힌 종이 크기 기준으로 정렬하면 접힌 상태에서의 괄호문자열이 됩니다.
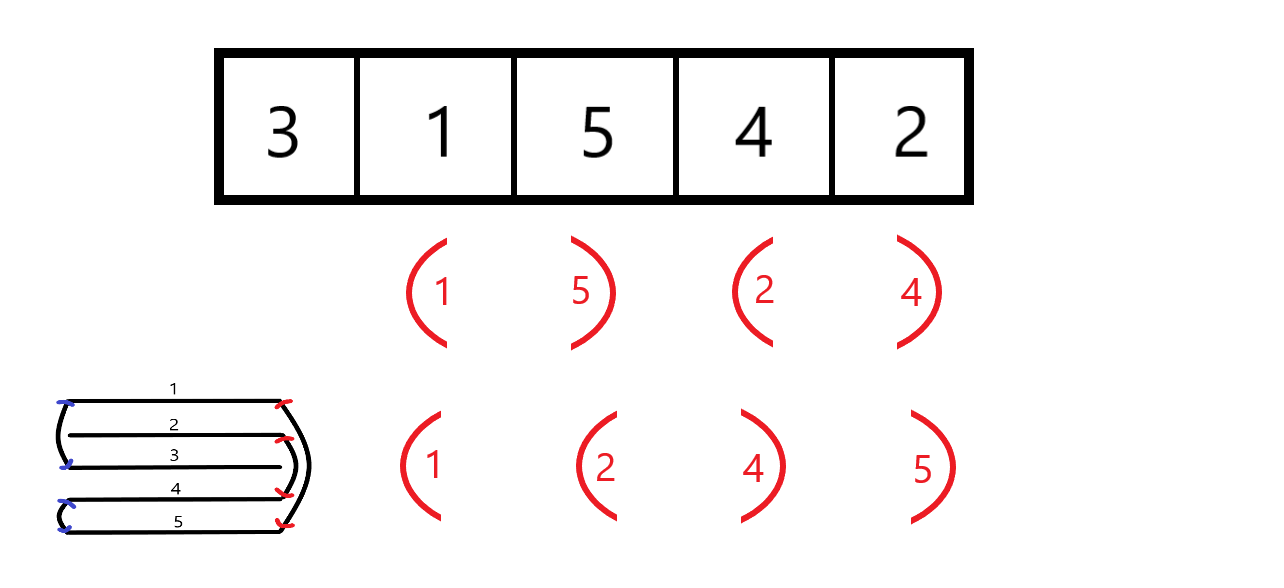
문제는 더욱 단순해졌습니다. 짝지어진 괄호들을 만들고, 이를 정렬하여 괄호문자열을 만듭니다. 그리고 유효성 검사를 해줍니다. 물론 이 과정은 좌우 두 번 이루어져야 합니다. 시간복잡도 \(O(N \log N)\)으로 해결할 수 있게 되었습니다. 또는, 단순히 접는 과정을 나이브하게 시뮬레이션하는 \(O(N^2)\)풀이도 있지만 발상과 접근은 일맥상통합니다.
예제 코드는 C로 짠데다가 문제의 목적에 맞게 여러 부분이 비약적으로 구성되어 있어 가독성이 크게 떨어집니다. 참고하세요.
#include <stdio.h>
#define LEN 2000
int N, A[LEN];
int sp, stack[LEN];
int seq[LEN];
int vps[LEN];
int temp[LEN]; // for sort
void merge(int l, int m, int r) { // 병합 정렬의 병합 함수
int i = l, j = m + 1, k = l;
while (i <= m && j <= r) temp[k++] = seq[vps[i]] < seq[vps[j]] ? vps[i++] : vps[j++];
while (i <= m) temp[k++] = vps[i++];
while (j <= r) temp[k++] = vps[j++];
for (k = l; k <= r; ++k) vps[k] = temp[k];
}
void merge_sort(int l, int r) { // 병합 정렬, 재귀적 구현
if (l == r) return;
int m = l + r >> 1;
merge_sort(l, m);
merge_sort(m + 1, r);
merge(l, m, r);
}
/* 괄호문자열 유효성 검사 함수
* 괄호는 0, 1, 2, ... 로 들어가고, 홀짝에 의해 방향이 결정됩니다.
* 실제 값 비교 시에는 2로 나눠서 괄호의 짝을 판단합니다.
* s[i]가 홀수라면(s[i] & 1): 닫힌 문자열입니다.
* 스택 맨 위의 원소와의 차가 0이 아니라면 옳게 짝지어지지 않은 것입니다.
* s[i]가 짝수라면 2로 나눈 값을 스택에 넣습니다.
*/
int check_vps(int* s, int len) {
int i;
sp = 0;
for (i = 0; i < len; ++i) {
if (s[i] & 1) {
if (!sp || stack[--sp] - (s[i] >> 1))
return 0;
}
else stack[sp++] = s[i] >> 1;
}
return 1;
}
int solve() {
int d, i, l, r, k, t;
scanf("%d", &N);
for (i = 0; i < N; ++i) scanf("%d", A + i);
for (d = 0; d < 2; ++d) { // 문자열은 좌우 2번 판단합니다.
for (i = 0; i < N; ++i) vps[i] = i; // 괄호는 0, 1, 2, ... 로 들어갑니다.
for (i = d, k = 0; i < N - 1; i += 2, k += 2) {
l = A[i], r = A[i + 1];
if (l > r) t = l, l = r, r = t; // swap
seq[k] = l, seq[k + 1] = r;
}
merge_sort(0, k - 1); // seq의 크기 기준으로 vps를 정렬합니다.
if (!check_vps(vps, k)) return 0;
}
return 1;
}
int main() {
int T;
scanf("%d", &T);
while (T--) printf("%s\n", solve() ? "YES" : "NO");
}