백준 17353 - 하늘에서 떨어지는 1, 2, ..., R-L+1개의 별
이번에도 세그먼트 트리 문제인 하늘에서 떨어지는 별입니다. 스위핑은 아니고, 세그먼트 트리 그 자체를 잘 응용할 수 있어야 하는 기발한 유형입니다. 뭘 구해야 하는지는 쉽게 알 수 있습니다. 일정 구간에 등차수열을 더하고, 한 점에 누적된 값을 찾으면 됩니다. 근데 이게 말처럼 쉬어야죠.
일정 구간에 값을 더하고 한 지점의 값을 구하는 것은 언뜻 보기엔 Lazy Propagation을 써야할 것 같지만, 실은 꼭 그런 것만도 아닙니다. 이 문제가 요구하는 게 바로 그런 유형인데요. 업데이트 쿼리가 들어오면 누적되는 구간을 쪼개서 각 노드에 값을 더해주고, 조회 쿼리가 들어오면 리프 노드가 되는 지점을 찾으면서 거쳐가는 노드의 값을 모두 더해주면 됩니다. 그냥 일반적인 세그먼트 트리로도 충분히 해결할 수 있게 됩니다.
typedef long long int ll;
const int MAX = 1'000'001;
int N;
ll arr[MAX];
ll seg_tree[MAX * 4];
void update(int left, int right, ll diff, int index = 1, int start = 1, int end = N) {
if (left > end || right < start) return;
if (start == end || left <= start && end <= right) {
seg_tree[index] += diff; return; // 구간에 걸쳐 값을 더해줍니다
}
int mid = (start + end) / 2;
update(left, right, diff, index * 2, start, mid);
update(left, right, diff, index * 2 + 1, mid + 1, end);
}
ll get(int n, int start = 1, int end = N, int index = 1) {
if (n > end || n < start) return 0; // 구간이 걸치지 않으면 0
if (start == end) return seg_tree[index] + arr[n]; // 지점 n부터 거슬러 올라갑니다
int mid = (start + end) / 2;
return seg_tree[index] + get(n, start, mid, index * 2) + get(n, mid + 1, end, index * 2 + 1); // 다 더해주기
}
이젠 등차수열 더하는 방법에 대해 좀 고민해봅시다. 가장 순진한 방법으로는 한 번의 등차수열 추가 업데이트에 대해, 구간 길이만큼의 구간 쿼리를 실시할 수 있습니다. 쿼리 \(Q(L, R)\)에 대해 \(Q(L + 1, R)\), \(Q(L + 2, R)\), … , \(Q(R - 1, R)\), \(Q(R, R)\)을 모두 수행해주는 거죠. 하지만 이렇게 되면 한 번의 쿼리가 \(O(N \log N)\)이 됩니다. 말이 안 되죠. 어떻게 하면 등차수열을 여러 번이 아닌 단 한 번에 세그먼트 트리에 담을 수 있을까요?
반대로 생각해봅시다. 어떤 등차수열의 가운데 \(k\)번째 값을 한 번만에 구할 수 있다면, 굳이 구간의 값들을 하나하나 바꿔줄 필요가 없게 됩니다. 등차수열의 임의의 \(k\)번째 값을 구하기 위해 필요한 건 딱 두 가지, 첫 번째 항 \(a_1\)과 공차 \(d\)입니다. 각 값을 저장하기 위해 세그먼트 트리 두 개를 쓰도록 하겠습니다. 점 \(x\)에 떨어진 별의 개수를 구하기 위해 세그먼트 트리를 조회한다고 할 때, \(x\)를 포함하는 임의의 구간 \([x_L, x_R]\) 노드의 시작 항 \(a_{x_L}\)과 공차 \(d_x\)를 안다고 할 때 점 \(x\)에 더해줘야 할 값은 다음과 같이 구할 수 있습니다:
\[n(x) = a_{x_L} + d_x(x - x_L)\]두 개의 값을 효율적으로 관리할 수만 있다면, 단 한 번의 업데이트로도 값을 정확히 구할 수 있게 됩니다. 문제는 그걸 어떻게 하느냐는 건데, 생각보다 간단합니다. 구간 업데이트 쿼리를 실시할 때, 공차는 무조건 1로 고정되므로 공차 세그먼트 트리의 노드는 \(1\) 더해주고, 첫 번째 항의 크기만 적당히 구해서 더해주면 됩니다. 업데이트하려는 구간 \([L, R]\)과 세그먼트 트리의 노드 \([x_L, x_R]\)에 대해, 만약 \(x_L\)이 \(L\)보다 작다면 이 노드는 구간을 완전히 포함하지 않게 됩니다. 따라서 업데이트되는 모든 노드에 대해서는 \(L ≤ x_L\)임을 가정할 수 있습니다. 이 때 첫 번째 항 \(a_{x_L}\)에 더해줘야 할 값은 \(x_L - L + 1\)이 됩니다. 예를 들어, \([2, 5]\) 구간 쿼리가 들어왔을 때는 다음 그림과 같이 됩니다.

구간 \([2, 2]\)에 대해 \(a_1 = 2 - 2 + 1 = 1\), 구간 \([4, 5]\)에 대해서는 \(a_1 = 4 - 2 + 1 = 3\)이 되는 식입니다. 여러 개의 등차수열이 더해져도 물론 문제 없습니다. \([3, 5]\) 구간 쿼리를 추가로 처리하면 다음과 같이 됩니다.
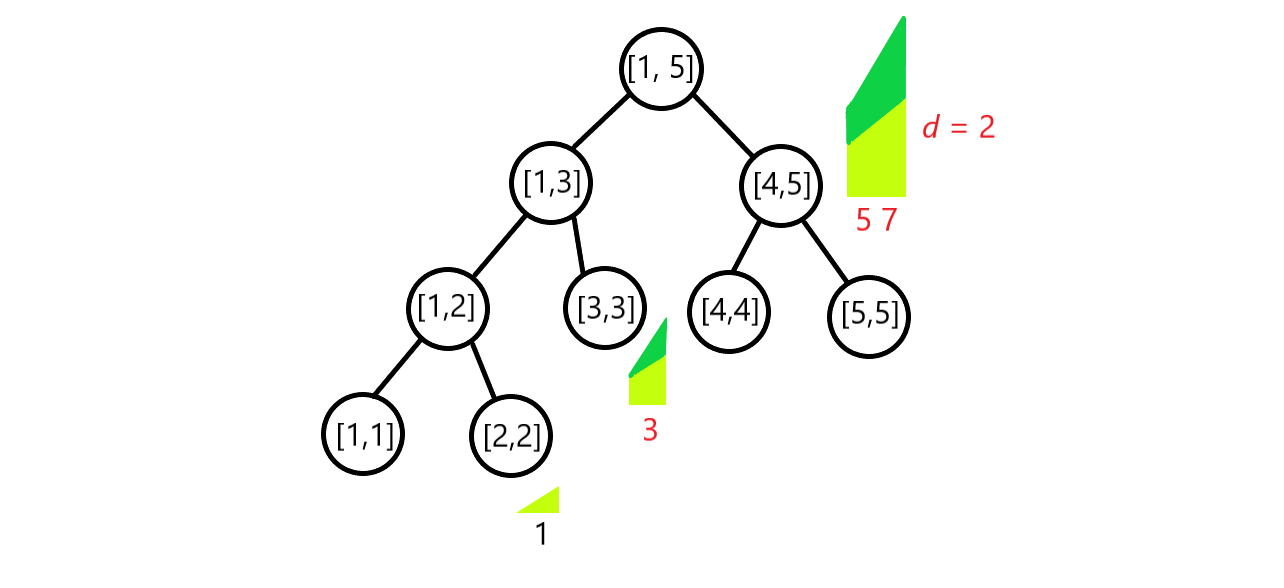
단 두 개의 값만 잘 관리해줘도 매우 정확하게 등차수열을 관리할 수 있게 되었습니다.
#include <iostream>
typedef long long int ll;
const int MAX = 100'001;
int N, Q;
ll arr[MAX];
ll seg_range[MAX * 4], seg_count[MAX * 4]; // 첫째 항, 공차 세그먼트 트리
void update(int left, int right, int index = 1, int start = 1, int end = N) {
if (left > end || right < start) return;
if (start == end || left <= start && end <= right) {
++seg_count[index]; // 이 문제에선 단순히 1 더해주면 됩니다.
seg_range[index] += start - left + 1; // 노드의 구간에 걸치는 첫 번째 항을 구해 더합니다. a1 += xL - L + 1
return;
}
int mid = (start + end) / 2;
update(left, right, index * 2, start, mid);
update(left, right, index * 2 + 1, mid + 1, end);
}
ll get(int n, int start = 1, int end = N, int index = 1) {
if (n > end || n < start) return 0;
if (start == end) return seg_range[index] + arr[n];
int mid = (start + end) / 2;
ll interval = n - start; // xL - L
ll count = seg_range[index] + seg_count[index] * interval; // n(x) = a1 + d * (xL - L)
return count + get(n, start, mid, index * 2) + get(n, mid + 1, end, index * 2 + 1);
}
int main() {
std::cin >> N;
for (int i = 1; i <= N; ++i) std::cin >> arr[i];
std::cin >> Q;
while (Q--) {
ll q, x, l, r;
std::cin >> q;
if (q == 1) {
std::cin >> l >> r;
update(l, r);
}
if (q == 2) {
std::cin >> x;
std::cout << get(x) << '\n';
}
}
}