백준 26157 - 즉흥 여행(Hard)

꾸준히 대회도 참가해 가면서 SSAFY 면접 준비가 한창입니다.

이번에 풀어볼 문제는 즉흥 여행입니다.

유향 그래프의 어떤 정점에서 시작하여 몇 번이고 같은 길을 갈 수 있다고 할 때, 모든 정점을 방문하는 것이 가능한지 확인하면 되는 어찌보면 간단해 보이는 문제입니다.

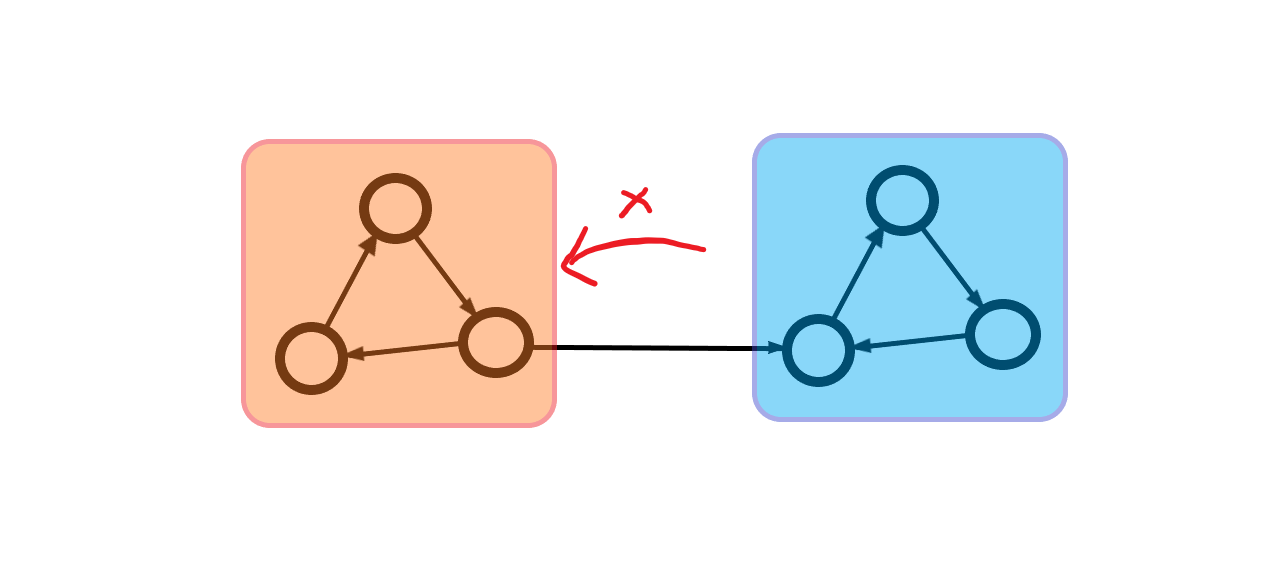
대회는 beginner와 Advanced로 나뉘어 진행되었고, easy 문제는 그냥 임의의 정점을 선택했을 때 전체를 방문할 수 있는지만 체크하면 되는 문제였죠. 강한 연결 요소로 정점들을 묶으면 사이클 없는 유향 그래프가 만들어지는데, 만약 연결 요소가 2개 이상이라면 임의의 정점에서 다른 정점으로 갈 수 없는 경우가 반드시 있습니다. 그 점을 이용하면 풀 수 있죠.

#include <iostream>
#include <vector>
#include <stack>
#include <algorithm>

const int MAX = 200'001;

std::vector<int> graph[MAX];
int checked[MAX];
std::vector<std::vector<int>> SCC;

int dfs(int v) { // 강한 연결 요소를 찾기 위해 정의된 dfs
	static int idx = 1, order[MAX];
	static std::stack<int> _stack;
	order[v] = idx++;
	int parent = order[v];
	_stack.push(v);
	for (const int& u : graph[v]) {
		if (!order[u]) parent = std::min(parent, dfs(u));
		else if (!checked[u]) parent = std::min(parent, order[u]);
	}
	if (parent == order[v]) { // cycle
		std::vector<int> scc;
		while (true) {
			int e = _stack.top(); _stack.pop();
			scc.push_back(e);
			checked[e] = true;
			if (e == v) break;
		}
		std::sort(scc.begin(), scc.end());
		SCC.push_back(scc);
	}
	return parent;
}

int main() {
	int V, E;
	std::cin >> V >> E;

	while (E--) {
		int a, b;
		std::cin >> a >> b;
		graph[a].push_back(b);
	}

	for (int i = 1; i <= V; ++i) {
		if (!checked[i]) dfs(i);
	}

	std::cout << (SCC.size() == 1 ? "Yes" : "No"); // 연결 요소의 수가 1개를 넘으면 No
}

이제 좀 더 논의를 진행해보겠습니다.

Hard 문제에서 요구하는 것은 어떤 점에서 출발했을 때 모든 점을 방문할 수 있는지를 확인하고 가능한 모든 출발점을 찾는 것입니다. SCC를 찾는 것에서 좀 더 나아갈 필요가 있는 것이죠.

사실 대회에선 이 문제를 맞히긴 했습니다. 비약이 심한 논리긴 하지만요.

만약 출발점 또는 도착점이 2개 이상이라면 모든 점을 방문하는 것은 불가능하다.

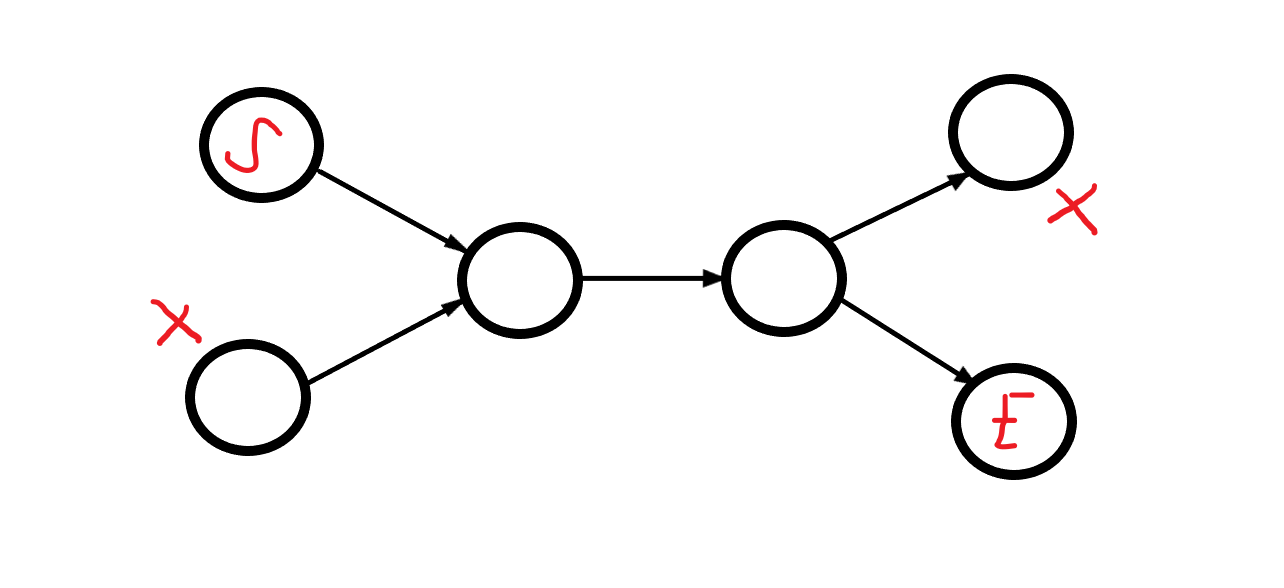
이 명제는 참입니다. 그럼 이렇게 생각해볼 수 있죠.

출발점과 도착점이 한 개씩 있다면 모든 점을 방문할 수 있을 것 같다.

이걸 토대로 코드를 짜면 다음과 같습니다.

#include <iostream>
#include <vector>
#include <stack>
#include <algorithm>

const int MAX = 200'001;

std::vector<int> graph[MAX];
int checked[MAX];

std::vector<std::vector<int>> SCC;
std::vector<int> graph_SCC[MAX];
int group[MAX];
int incoming[MAX];
int outgoing[MAX];

int dfs(int v) {
	static int idx = 1, order[MAX];
	static std::stack<int> _stack;
	order[v] = idx++;
	int parent = order[v];
	_stack.push(v);
	for (const int& u : graph[v]) {
		if (!order[u]) parent = std::min(parent, dfs(u));
		else if (!checked[u]) parent = std::min(parent, order[u]);
	}
	if (parent == order[v]) { // cycle
		std::vector<int> scc;
		while (true) {
			int e = _stack.top(); _stack.pop();
			scc.push_back(e);
			checked[e] = true;
			if (e == v) break;
		}
		std::sort(scc.begin(), scc.end());
		SCC.push_back(scc);
	}
	return parent;
}

int main() {
	int V, E;
	std::cin >> V >> E;

	while (E--) {
		int a, b;
		std::cin >> a >> b;
		graph[a].push_back(b);
	}

	for (int i = 1; i <= V; ++i) {
		if (!checked[i]) dfs(i);
	}

	if (SCC.size() == 1) {
		std::cout << SCC[0].size() << '\n';
		std::sort(SCC[0].begin(), SCC[0].end());
		for (const int& e : SCC[0]) std::cout << e << ' ';
	}
	else {
		for (int i = 0; i < SCC.size(); ++i) { // preporcess
			for (const int& e : SCC[i]) {
				group[e] = i;
			}
		}
		for (int i = 1; i <= V; ++i) {
			for (const int& e : graph[i]) {
				int from = group[i], to = group[e];
				if (from == to) continue;
				graph_SCC[from].push_back(to);
				incoming[to]++;
				outgoing[from]++;
			}
		}
		int start_point = -1, start_count = 0, end_count = 0;
		for (int i = 0; i < SCC.size(); ++i) {
			if (!incoming[i]) start_point = i, start_count++;
			if (!outgoing[i]) end_count++;
		}
		if (start_count > 1 || end_count > 1) std::cout << 0;
		else {
			std::cout << SCC[start_point].size() << '\n';
			std::sort(SCC[start_point].begin(), SCC[start_point].end());
			for (const int& e : SCC[start_point]) std::cout << e << ' ';
		}
	}
}

언뜻 생각해보면 그럴싸하긴 한데, 언제나 그렇듯 명제의 역과 이가 늘 참인 것은 아닙니다.

가장 단순한 반례는 어렵지 않게 찾을 수 있죠.

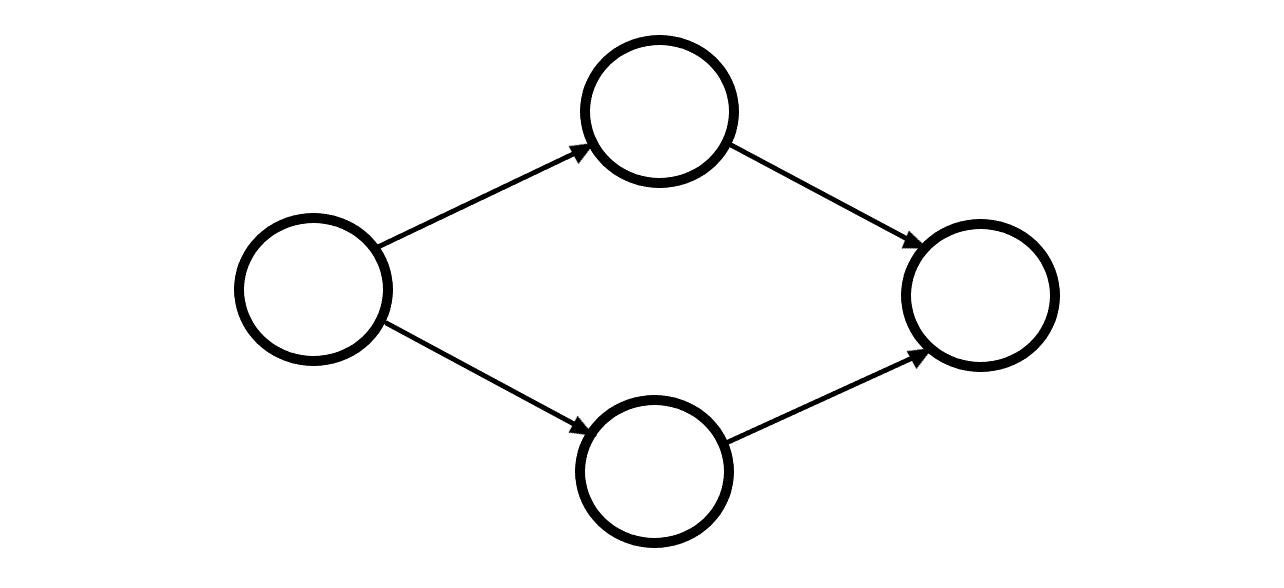
그렇습니다. 출발점과 도착점은 필요조건이지 충분조건은 아닌 겁니다. 모든 점을 살펴봐서 해밀턴 경로가 존재하는지를 확인해야 합니다. 모든 정점을 한 번씩만 방문하는 경로를 해밀턴 경로라고 하는데, 오일러 경로와는 달리 다항 시간 내에 이를 찾아내는 알고리즘은 아직 밝혀지지 않았습니다. 네, 이건 NP 문제라는 거죠. 하지만 다행히도 강한 연결 요소로 묶어주는 처리를 했고, 연결 요소 내에서는 정점을 두 번 이상 방문해도 상관이 없다는 문제의 특성 덕분에 \(O( \left| V \right| )\)로 해밀턴 경로 존재 유무를 확인할 수 있습니다.

#include <iostream>
#include <vector>
#include <stack>
#include <queue>
#include <set>
#include <algorithm>

const int MAX = 200'001;

std::vector<int> graph[MAX];
int checked[MAX];

std::vector<std::vector<int>> SCC;
std::set<int> graph_SCC[MAX];
int group[MAX];
int incoming[MAX];
int depth[MAX];
int start_point;
int V, E;

int dfs(int v) {
	static int idx = 1, order[MAX];
	static std::stack<int> _stack;
	order[v] = idx++;
	int parent = order[v];
	_stack.push(v);
	for (const int& u : graph[v]) {
		if (!order[u]) parent = std::min(parent, dfs(u));
		else if (!checked[u]) parent = std::min(parent, order[u]);
	}
	if (parent == order[v]) { // cycle
		std::vector<int> scc;
		while (true) {
			int e = _stack.top(); _stack.pop();
			scc.push_back(e);
			checked[e] = true;
			if (e == v) break;
		}
		std::sort(scc.begin(), scc.end());
		SCC.push_back(scc);
	}
	return parent;
}

int topological_sort() { // 위상 정렬을 시행하여, 시작점으로부터 거쳐간 정점의 수를 확인합니다.
	int max_count = 1;
	for (int i = 0; i < SCC.size(); ++i) { // preporcess
		for (const int& e : SCC[i]) {
			group[e] = i;
		}
	}
	for (int i = 1; i <= V; ++i) {
		for (const int& e : graph[i]) {
			int from = group[i], to = group[e];
			if (from == to) continue;
			if (graph_SCC[from].find(to) == graph_SCC[from].end()) {
				graph_SCC[from].insert(to);
				incoming[to]++;
			}
		}
	}
	std::queue<int> Q;
	for (int i = 0; i < SCC.size(); ++i) {
		if (!incoming[i]) {
			start_point = i;
			depth[i] = 1;
			Q.push(i);
		}
	}
	while (!Q.empty()) {
		int u = Q.front(); Q.pop();
		for (const int& v : graph_SCC[u]) {
			if (!--incoming[v]) {
				depth[v] = depth[u] + 1;
				max_count = std::max(depth[v], max_count);
				Q.push(v);
			}
		}
	}
	return max_count;
}

int main() {
	std::cin >> V >> E;

	while (E--) {
		int a, b;
		std::cin >> a >> b;
		graph[a].push_back(b);
	}

	for (int i = 1; i <= V; ++i) {
		if (!checked[i]) dfs(i);
	}
    // 시작점에서 거쳐간 정점 수의 최대값이 정점의 수와 같다면 해밀턴 경로가 존재합니다.
	if (topological_sort() == SCC.size()) { 
		std::cout << SCC[start_point].size() << '\n';
		std::sort(SCC[start_point].begin(), SCC[start_point].end());
		for (const int& e : SCC[start_point]) std::cout << e << ' ';
	}
	else std::cout << 0;
}