아무도 못 푼 문제 - 작업공정
실제로 풀어보고 글을 쓴다면 좋겠지만, 일단 손 대본 문제라서 한 번 써봅니다.
이번에 풀어볼 문제는 작업공정입니다.
어떤 회사의 작업공정은 아래에서 위로 진행됩니다. 밑의 직원들이 일을 모두 끝내야 상사가 작업을 전달받아 할 수 있는 방식입니다. 각 직원에게는 한 명의 직속 상사만 있으며, 모든 작업은 단위 시간이 걸립니다. 이제 회사에서 일부 직원을 해고하려 할 때 최소 작업 완료 시간과, 원래의 작업시간을 유지하면서 해고할 수 있는 최대 인원 수를 구하세요.
일단 문제를 읽어보니 회사 형태는 트리 그래프로 그려지겠습니다.
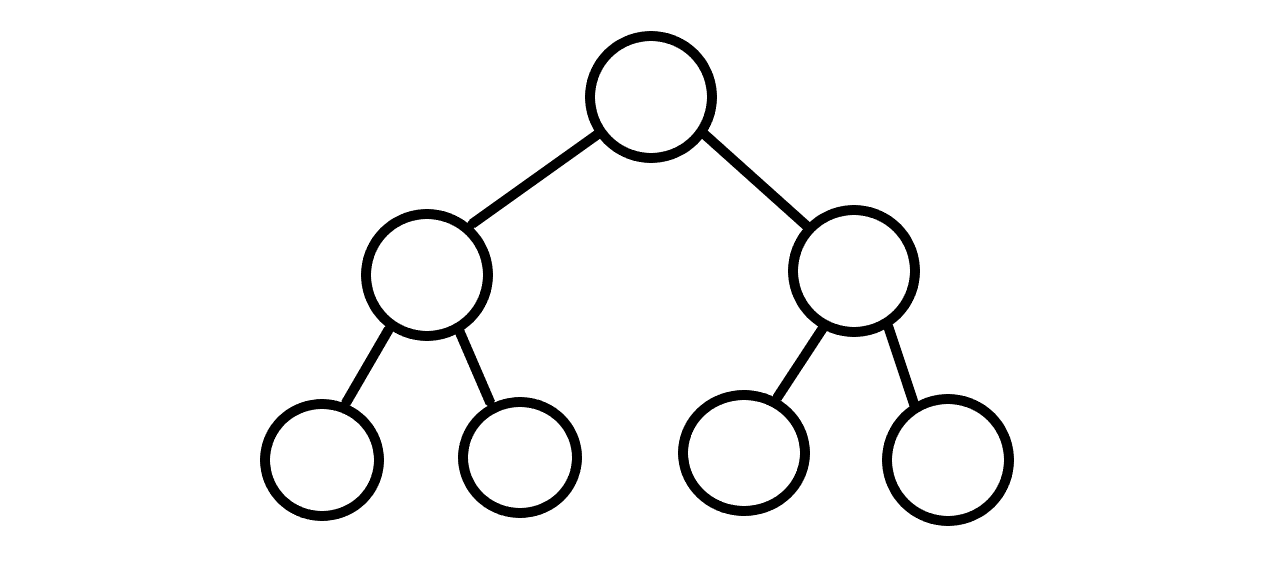
위 그래프는 예제를 나타낸 것입니다. 원래 최소 작업 완료 시간은 트리의 높이가 되겠군요. 모든 작업에 단위 시간 1이 소요된다고 할 때, 최소 작업 완료 시간은 결국 루트 노드에서 가장 멀리 떨어진 리프 노드의 깊이입니다. (루트를 1부터 계산) 예제에서 작업 완료 시간은 3입니다.
이제 남은 문제는 최소 인원을 찾는 건데, 이건 한참을 고민해야 했습니다.
음, 그냥 특정 레벨에 노드 수가 가장 많다면 그게 최소 인원 아닐까? 예제로 보자면 말단 업무가 4개니까 4명 남기고 다 해고하면 되겠네요.
하지만 그게 그리 쉬운 일이 아니었습니다.
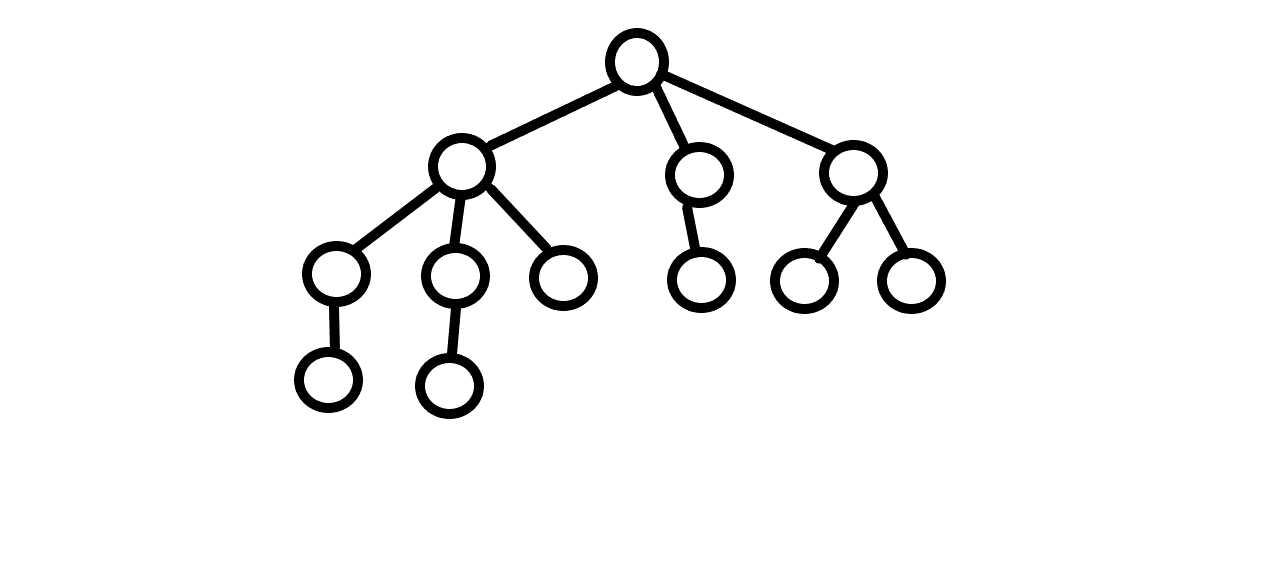
위 그래프에서 특정 레벨에서 가장 많은 노드의 수를 찾으면 6입니다. 하지만 약간의 변형을 거치면…
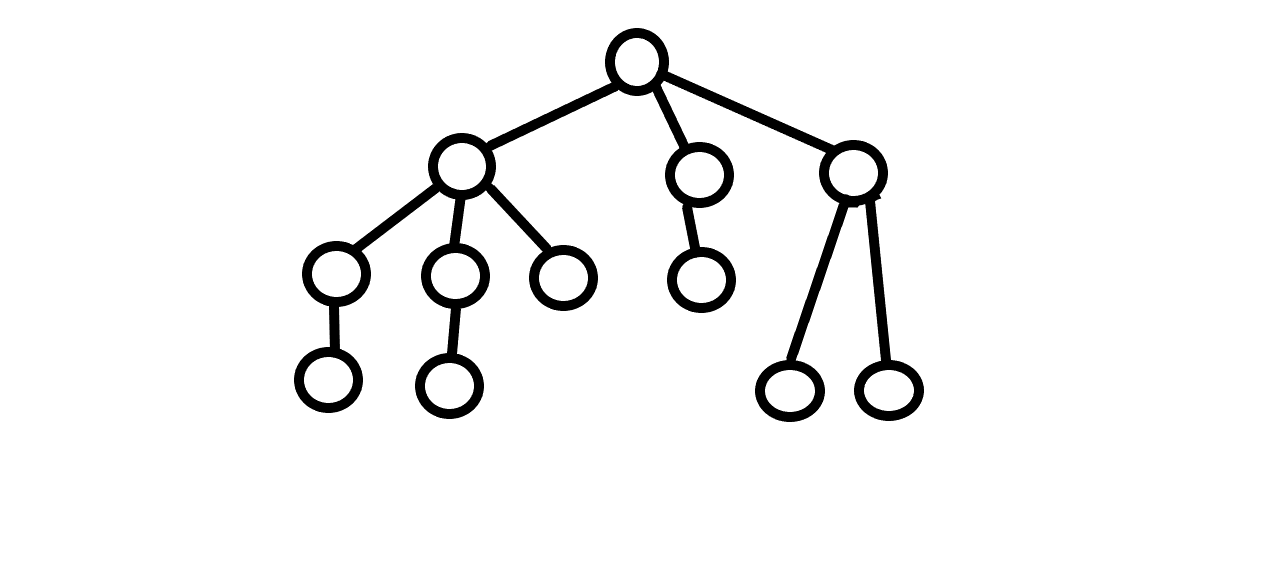
4명만 있어도 최소 작업 완료 시간 내에 모든 작업을 할 수 있게 됩니다. 단순히 어떤 조건을 만족하는 노드의 수를 찾는 건 정답이 될 수는 없었습니다.
그럼 일단 노드를 깊이 순으로 넣어놓고 하나하나 옮겨봐야 할까, 하는 초보적인 방식도 떠올려보다가 하나 떠오른 생각이 있었죠.
방법은 단순합니다. 주어진 트리에 대해, 리프 노드를 모두 골라냅니다. 그리고 깊이가 깊은 순으로 제한된 인원 수 만큼 작업을 실시합니다. 그리고 완료된 작업 노드를 제거한 후, 다시 리프 노드를 고르고, 깊이 순으로 작업을 해줍니다. 그리고 이 절차를 반복하여 모든 작업이 완료될 때까지 걸린 시간이 바로 최적 작업 완료 시간 아닐까요.
일단 예시 그래프에서 3개씩 작업을 해낸다고 해봅시다.




최소 작업 완료 시간 내에 모든 노드를 제거하지 못했습니다. 이번엔 4개씩 해봅시다.




성공입니다! 이 그래프의 최소 인원 수는 4입니다.
그런데 문제는 이겁니다.
인원 \(K\)로 최소 작업 시간 내 완료가 가능하다와 최소 작업 시간 내에 완료되면 \(K\)는 최소 인원 수이다라는 명제는 동치가 아닙니다. 인원 수 \(K\)는 최소 인원이다와 인원 수 \(K\)로 항상 최소 작업 시간 내 완료가 가능하다도 또한 동치가 아닐 가능성은 있죠.
결국 논리의 허점에 막혀 허우적대던 차에 논문 하나를 발견했으니, 바로 Hu의 스케줄링입니다.
Hu's algorithm을 적용하기 위한 조건은 다음과 같습니다:
- DAG여야 한다. (Directed Acyclic Graph, 방향 있는 트리는 DAG임)
- 모든 작업의 소요 시간은 동일한 단위여야 한다. (문제의 모든 작업은 단위 시간 1 소요)
- 모든 작업은 임의의 프로세서에 배정 가능하다. (문제의 작업은 상사, 부하 다 할 수 있음)
모든 조건이 부합하니, 스케줄링을 하면 되겠군요.
스케줄링 방법은 제가 떠올린 방법과 같습니다. 우선순위대로 집어넣는 탐욕법으로 진행됩니다.
IBM 연구원이 고안한 이 알고리즘은 특정 작업 용량으로 스케줄링을 할 때 최적 시간 내 작업이 완료됨을 보장합니다. Hu의 원 논문에선 상당히 복잡한 수식으로 증명되어 있는데, McHugh의 논문에선 훨씬 단순하게 증명되어 있습니다.
인원 \(K\)로 항상 최적 작업 완료 시간 내 완료 가능하므로 이제 \(K\)가 최소 필요 인원일 때, 항상 최소 작업 완료 시간 내 완료 가능하다라는 명제는 참이 되었습니다. 최소 필요 인원은 이분 탐색으로 찾아줍시다.
스케줄링은 위상정렬로 뼈대를 만들어놓고 껍데기를 씌우는 식으로 할 겁니다.
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
#include <cstring>
#include <cmath>
const int MAX = 100'001;
std::vector<int> tree[MAX];
int level[MAX]; // Hu 알고리즘에서의 label에 해당합니다.
int tree_width[MAX];
int incoming[MAX];
std::vector<int> graph[MAX];
int N;
struct Comp { // Hu 스케줄링을 하기 위해서는 트리에서 깊이가 깊은 순으로 작업을 처리해야 합니다.
bool operator()(int a, int b) { return level[a] < level[b]; }
};
void make_tree(int v = 0, int height = 0) { // 노드의 깊이를 구해야 하므로 일단 트리를 만듭니다.
level[v] = height;
++tree_width[height];
for (const int& u : tree[v]) {
make_tree(u, height + 1);
}
}
/// <summary>
/// 조건부 위상정렬 (Hu's algorithm)
/// <para>O(N log N)</para>
///
/// 동시간 처리 가능한 일의 수만큼만 정렬함.
/// 또한, 트리에서의 노드 깊이 순 우선순위에 따라 정렬함.
/// </summary>
/// <param name="capacity">동시간 해결할 수 있는 업무의 수(직원의 수)</param>
/// <returns>경과 시간</returns>
int conditional_topological_sort(int capacity) {
std::priority_queue<int, std::vector<int>, Comp> delayed; // 대기열 큐
std::queue<int> Q; // 프로세서 큐
static int currentIncoming[MAX];
int time = 0;
memcpy(currentIncoming, incoming, sizeof incoming);
for (int i = 1; i <= N; ++i) {
if (!currentIncoming[i])
delayed.push(i); // 모든 리프노드를 일단 대기열에 추가합니다.
}
while (!delayed.empty()) {
for (int i = 0; i < capacity && !delayed.empty(); ++i) { // 작업 용량 만큼
Q.push(delayed.top()); delayed.pop(); // 매 단계마다 우선순위가 높은 것부터 프로세서에 할당합니다.
}
while (!Q.empty()) {
int v = Q.front(); Q.pop();
for (const int& u : graph[v]) {
if (!--currentIncoming[u]) {
delayed.push(u); // 작업 완료 후 리프노드가 된 작업은 대기열에 넣습니다.
}
}
}
++time; // 각 단계마다 시간이 경과합니다.
}
return time; // 최적 작업 완료 시간을 반환합니다.
}
/// <summary>
/// 이분탐색
/// <para>O(log N) * O(N log N)</para>
///
/// 총 경과 시간은 트리의 높이 이하여야 한다.
/// </summary>
/// <param name="width">트리의 폭</param>
/// <param name="height">트리의 높이</param>
/// <returns>직원의 최소 수</returns>
int binary_search(const int width, const int height) {
int l = ceil(double(N) / height), r = width + 1, result = width + 1;
while (l <= r) {
int mid = (l + r) / 2;
int val = conditional_topological_sort(mid); // 스케줄링에 걸리는 최적 작업 완료 시간을 구합니다.
if (val <= height) { // 최적 작업 완료 시간이 최소 작업 완료 시간 이하라면 (필요 인원)
result = std::min(result, mid); // 최소 인원인지 확인합니다.
r = mid - 1; // 인원을 줄여 다시 검사합니다.
} // 최적 작업 완료 시간이 최소 작업 완료 시간보다 길다면
else l = mid + 1; // 인원을 늘려 다시 검사합니다.
}
return result; // 최소 필요 인원을 반환합니다.
}
int main() {
std::cin >> N;
for (int a, i = 1; i <= N; ++i) {
std::cin >> a;
if (a == -1) {
tree[0].push_back(i);
}
else {
tree[a].push_back(i);
graph[i].push_back(a);
++incoming[a];
}
}
make_tree(); // 트리를 만듭니다.
int height = *std::max_element(level, level + N + 1); // 트리의 높이(깊이)를 구합니다.
int width = *std::max_element(tree_width, tree_width + N + 1); // 이분탐색 최적화
int result = binary_search(width, height); // (해고 가능 인원) = (총원) - (최소 필요 인원)
std::cout << height << '\n' << N - result; // 최소 작업 완료 시간과 해고 가능 인원을 출력합니다.
}위 알고리즘은 시간복잡도 면에서 비교적 저렴한 편에 속하는 이분탐색, 위상정렬, 우선순위 큐로만 이루어져 있습니다. 실제 시간복잡도는 \(O(N \log^2 N)\)로, TLE를 받을 정도는 아닙니다.
예제는 어찌저찌 잘 통과하는데, 안타깝게도 이 코드는 통과하지 못했습니다. 혹시 어떤 조건이 잘못된 게 아닌가 싶어 여기저기 assert까지 집어넣어봤으나 그런 건 아닌 것 같습니다. 연구원들조차 알지 못했던 기막힌 반례라도 있는 건지 아니면 제가 문제를 잘못 이해하고 있는 것인지조차 헷갈리기 시작하는군요. 틈날 때마다 코드를 손봐서 제출해봤지만, 아무래도 통과할 기미가 보이지 않습니다.