백준 25921 - 건너 아는 사이
연세대 프로그래밍 대회에 참가했습니다. 16위에 그쳤지만, 몇 문제라도 풀었다는 것에 만족하며 더욱 발전해야겠죠.
이번에 풀어볼 문제는 건너 아는 사이입니다.
사람들 사이의 네트워크, 즉 몇 다리 걸치면 아는 사이라는 말이 있죠. 이번 문제는 아주 간단하게, 바로 이 네트워크를 구성하는 최소 비용을 구하는 문제입니다.
네트워크의 각 정점을 연결할 간선을 추가하기 위한 조건은 다음과 같습니다.
- 두 사람의 번호가 서로소일 때, 두 번호 중 큰 값이다. 서로소란 두 수 사이에 1 이외의 공약수가 없음을 의미한다.
- 두 사람의 번호가 서로소가 아닐 때, 두 번호의 최대공약수이다.
언뜻 문제를 읽어보니 퍼뜩 드는 생각은 최소 신장 트리를 구하는 것이었죠. 크루스칼 알고리즘을 적용해보려 하니 시간복잡도가 걸림돌입니다. 간선의 수를 \(E\)라 할 때 \(O(E\log E)\)입니다. 문제에서 주어진 정점의 수가 \(N=1,000,000\)이고 모든 정점 사이엔 임의의 간선을 놓을 수 있으니까 \(E=N(N - 1)/2\)… 어림도 없군요!
다시 생각해봐야 합니다. 어떻게 최소 신장 트리를 구할 것인지가 아니라, 그 최소 신장 트리가 어떻게 생겨먹은 놈인지를 본질적으로 따져본다면 풀이 방식은 더 단순해질 수 있죠.
귀납적으로 생각해보겠습니다.
\(N = 1\)일 때, 비용은 \(0\)입니다.
\(N = 2\)일 때, \(1\)과 \(2\)를 잇는 비용은 (서로소이므로) \(2\)입니다.
\(N = 3\)일 때도 \(1\)과 \(2\)는 모두 서로소입니다. 만일 현재 열결된 두 정점 간의 간선을 끊고 새로운 간선 2개를 추가한다면 총 비용은 \(6\)이 됩니다. 그냥 새 간선만 추가한다면 추가 비용은 \(3\)이고 총 비용은 \(5\)입니다.
\(N = 4\)일 때는 계산이 약간 달라집니다. \(2\)와 \(4\)의 최대공약수는 2입니다. 임의의 간선을 끊고 \(4\)번 정점에 간선을 두 개 추가한다면 그 어느 경우에도 비용은 2보다 큽니다.
이제 논의를 \(N = K\)일 때로 옮겨봅시다.
만일 \(K\)가 소수라면: 최소 비용으로 연결된 네크워크 \(K-1\)의 임의의 간선을 끊고 \(K\)에 간선을 2개 연결하면 추가되는 비용은 무조건 \(K\)보다 큽니다. 최소 신장 트리 \(K-1\)에 존재하는 모든 간선의 가중치 값은 \(K-1\)보다 같거나 작을 수 밖에 없으므로
\[2K - (K - c) = K + c > K (c > 0)\]따라서 최소 신장 트리 \(K - 1\)는 그대로 두고 새 간선 \(K\)를 추가하는 것이 가장 저렴합니다.
만일 \(K\)가 소수가 아니라면: 최소 비용으로 연결된 네크워크 \(K - 1\)의 임의의 간선을 끊고 \(K\)번 정점에 두 개의 간선을 추가할 때, 값이 최소가 되기 위한 조건은 다음과 같습니다:
- 기존에 연결되어 있던 두 정점과 새 정점 \(K\)의 최대 공약수가 같다.
그리고 이 조건이라면 그 두 정점 중 하나에 \(K\)를 갖다붙여도 비용은 같습니다.
이제 기존의 간선을 끊지 않고 그냥 갖다붙일 정점을 골라봅시다. 이건 별로 어렵지 않은데, 그냥 \(K\)의 가장 작은 소인수를 골라 붙이면 됩니다.
정리해봅시다. \(K\)가 소수라면 아무 정점에나 갖다붙여도 비용은 \(K\)이므로 그냥 1에 붙이겠습니다. \(K\)가 소수가 아니라면 가장 작은 소인수에 붙입니다. 머릿속에 그려지시나요? \(1\)이 중심에 있고, 그 주위로 소수가 주욱 붙어있습니다. 그리고 그 소수를 허브로 하여 배수가 주욱 붙어있는 모양입니다.
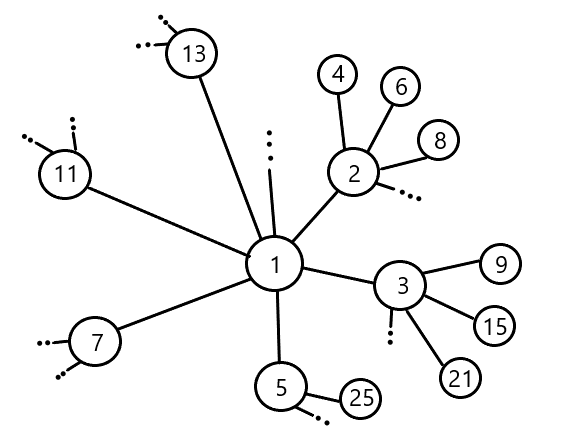
이제 문제를 좀 더 간단히 다룰 수 있게 되었습니다. \(2\)부터 \(N\)까지 모든 수의 가장 작은 소인수의 합을 구하면 되겠군요.
여기서 써먹을 수 있는 게 뭐가 있을까요? 바로 에라토스테네스의 체입니다. 원래는 소수를 찾는 알고리즘인데, 하나의 소수를 찾는 과정에서 그 배수를 모두 찾아 지운다는 점을 역으로 이용할 겁니다.
일단 \(2\)를 \(1\)에 붙입시다. 그리고 짝수는 모두 찾아 \(2\)에 붙입니다. 그 과정에서 총 비용에 \(2\)를 계속해서 추가합니다. \(3\)을 \(1\)에 붙이고, 남은 수 중에서 3의 배수를 찾아 \(3\)에 붙입니다. 총 비용에 \(3\)을 계속 추가합니다. \(N\)보다 같거나 작은 모든 소수 \(p\)에 대해 이 과정을 반복합니다.
이 과정은 에라토스테네스의 체와 완전히 동일하게 작동합니다. 그리고 여기서 한 가지 짚고 넘어갈 것은, 이 과정이 크루스칼 알고리즘과도 완전히 동일하게 작동한다는 겁니다. 간선의 가중치는 소수이고, 필연적으로 소수는 정렬되어 있습니다. 간선 크기 순으로 정렬하고 탐욕적으로 정점을 연결하는 알고리즘의 성질이 일맥상통하는 것이죠.
이제 시간복잡도는 \(O(E \log E)\)가 아니라 \(O(N \log \log N)\)-에라토스테네스의 체-가 되었습니다.
#include <cstdio>
typedef long long int ll;
int main() {
ll N, cost = 0;
scanf("%d", &N);
bool A[N + 1] = {0}; // 원래는 에라토스테네스의 체입니다만, 일종의 visited로도 볼 수 있습니다.
for (int i = 2; i <= N; ++i) {
if (A[i]) continue;
for (int j = i; j <= N; j += i) {
if (A[j]) continue;
A[j] = true; // 간선을 연결했다면 방문 체크를 합니다.
cost += i; // 간선 비용을 추가합니다.
}
}
printf("%lld", cost);
}