아무도 못 푼 문제 - biggest
이번에 리뷰해볼 문제는 biggest입니다. 조금 색다른 컨텐츠로, 아무도 못 푼 문제나 매니악한 문제를 다뤄볼까 합니다.
문제가 영어로 되어있어서 그런데, 그냥 알기 쉽게 의역을 좀 해보겠습니다.
\(N\)개의 무게가 서로 다른 구슬이 있습니다. 그중에서 무거운 순서대로 \(K\)개를 골라내려 합니다. 구슬의 무게를 알 수 있는 방법은 없고, 단지 양팔저울의 양 그릇에 구슬을 하나씩 올려서 무게를 비교해볼 수밖에 없습니다. 저울을 가능한 한 적게 써서 \(K\)개를 골라낸 결과를 반환하는 함수 biggest를 작성하세요.
단, 구슬의 무게를 비교하는 함수는 헤더 biggest.h의 함수 compare(int, int)를 써야 하고, 소스코드의 머리에 이 헤더를 include해야 합니다.
성공적으로 \(K\)개를 골라냈다면 부분점수를 얻을 수 있습니다. 저울은 얼마든지 사용할 수 있습니다만, 3백만 번이 넘게 되면 0점 처리됩니다. 또한 심판이 모종의 방법으로 \(K\)개를 골라냅니다. 당신이 얻는 점수는 다음 식으로 계산됩니다. (\(yourScore\): 당신의 구슬 비교 횟수, \(authorScore\): 심판의 구슬 비교 횟수, 구슬 비교 횟수는 처음 \(N - 1\)번은 세지 않습니다)
\[score = min(1, (authorScore + 1) / (yourScore + 1))\]코드 작성 규칙이 좀 까다롭지만, C++을 제대로 배운 사람이라면 이정도는 그냥저냥 할 수 있는 수준이죠.
코드 작성보다 더 문제인 것은, 대체 이 문제를 어떻게 풀 것인가 하는 겁니다. 저울을 가능한 한 적게 써야겠다는 것은 알겠습니다. 그런데 그게 가능이나 한 걸까요?
일단 논의를 옮겨, 가장 무거운 구슬을 어떻게 찾을지부터 생각해봅시다. 이건 생각보다 쉽게 답을 찾을 수 있습니다. 다음처럼 하면 됩니다.
- 구슬 2개를 골라 무거운 쪽을 골라냅니다. (1회 비교)
- 나머지 \(N - 2\)개의 구슬 중 하나를 골라 무거운 쪽과 비교, 다시 무거운 쪽을 골라냅니다.
- 더이상 비교할 구슬이 없을 때까지 반복합니다. (\(N - 2\)회 비교)
총 \(N - 1\)회 비교하면 가장 무거운 구슬을 골라낼 수 있습니다.
그리고 남은 \(N - 1\)개의 구슬에 대해, \(N - 2\)회 비교로 두 번째로 무거운 구슬을 골라낼 수 있죠. 다음은 \(N - 3\), 다시 \(N - 4\)… \(N\)개의 구슬을 이런 방식으로 정렬하게 되면
\[\sum_{k=1}^{N-1}k = N(N-1)/2\]번 비교하면 됩니다. \(1\)부터 \(N - 1\)까지 다 더한 수가 나옵니다.
하지만 이 방식으로는 구슬이 조금만 많아져도 문제가 생깁니다. 저울의 사용 횟수 제한은 3백만 번인데, 구슬이 3천 개쯤 되면 이미 사용 횟수는 5백만 번에 가까워집니다. \(N\)은 최대 10만이니까 이 방식으로는 절대 정렬을 할 수 없습니다. 다른 방법을 찾아야 합니다.
이렇게 생각해보면 어떨까요? \(N - 1\)번 비교를 할 동안, 최대한 많은 양의 정보를 얻어내는 겁니다. 그리고 다음번 비교에서 이를 활용할 수 있으면 좋겠는데요. CS 공부를 좀 해본 사람이라면 퍼뜩 떠오르는 게 있으니, 바로 트리입니다.
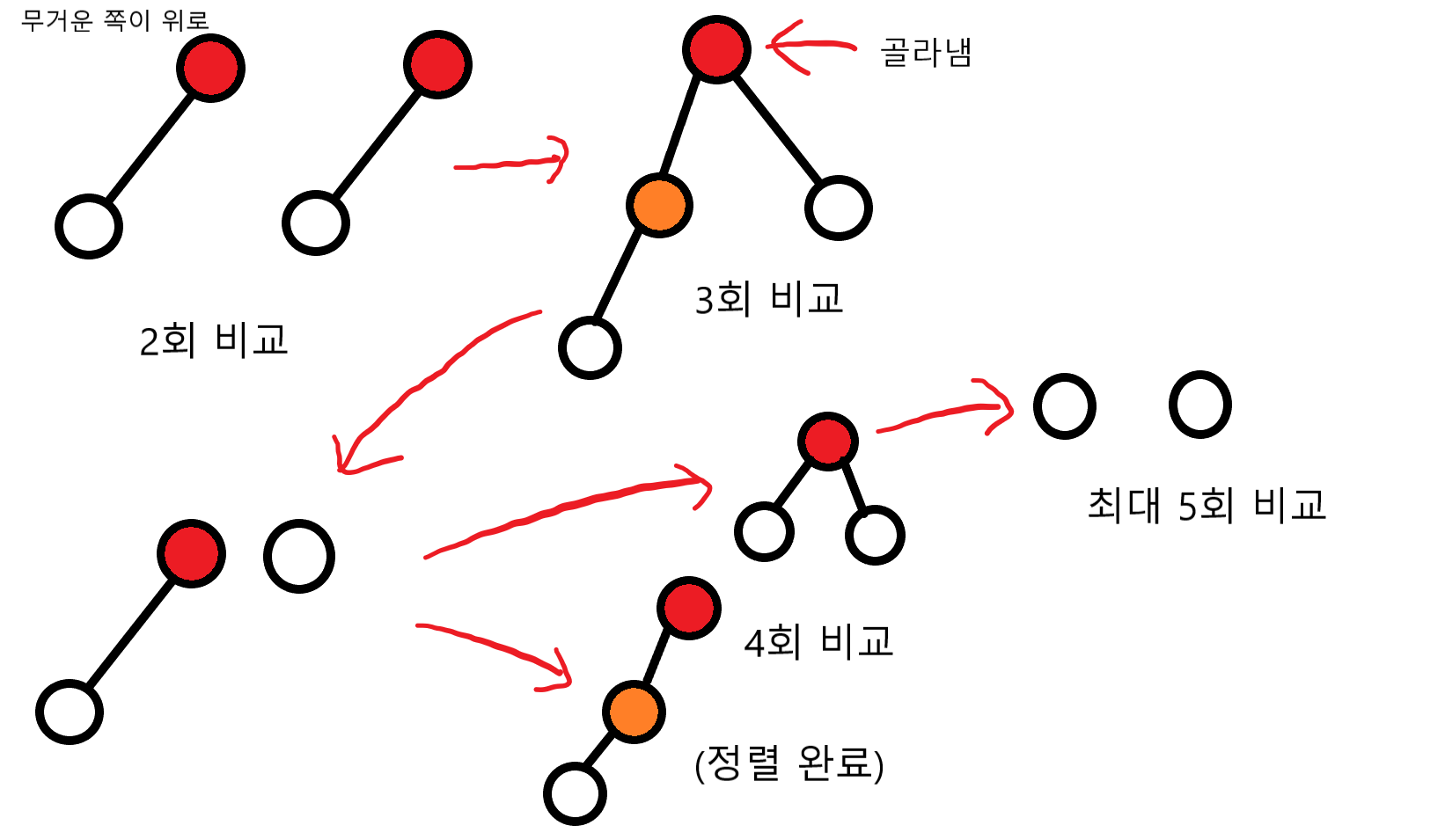
구슬 4개를 예로 들어봅시다. 처음 가장 무거운 구슬을 3번 비교하여 골라낸 후 3개가 남을 때, 아무 정보도 없다면 다시 2번, 그리고 또 1번 비교해서 정렬을 할 수 있습니다. 하지만 위 그림처럼 골라내면 5번만에 정렬할 수 있습니다.
- 2개씩 짝을 지어 비교합니다. (2회)
- 더 무거운 구슬끼리 다시 짝을 지어 비교합니다. (1회)
- 가장 무거운 구슬을 골라낸 후 남은 것은 짝 하나와 구슬 하나입니다. 짝에서 더 무거운 쪽과 남은 구슬 하나를 비교합니다. (1회)
- 남은 구슬이 더 무겁다면 정렬이 완료되었습니다. 남은 구슬 쪽이 더 가볍다면 가장 무거운 구슬을 골라내고 남은 2개를 마저 비교합니다. (최대 5회)
이 절차는 마치 트리를 만드는 것처럼 이루어집니다. 각 정점은 구슬에 해당합니다. 그리고 간선은 두 정점 간 비교가 되었다는 뜻이죠. 간선의 부모 쪽이 더 무겁고, 자식 쪽이 더 가볍습니다. 그리고 놀랍게도, 트리의 간선 수는 \(N - 1\)입니다. 문제에서 처음 \(N - 1\)회는 세지 않는다고 했으니, 어떤 형태로든 트리를 만들라는 뜻으로 해석할 수도 있는 거죠.
이제 구슬 4개에서 논의를 좀 더 확장해봅시다.
다음 방식으로 트리를 만들겠습니다.
- 짝을 지어 구슬을 비교하여 무거운 구슬을 골라냅니다.
- 무거운 구슬들을 모두 모아 다시 짝을 이룹니다.
- 무거운 구슬이 하나 남을 때까지 1번으로 돌아가 반복합니다.
이런 식으로 알고리즘을 돌리면 한정된 형태의 트리가 만들어집니다.
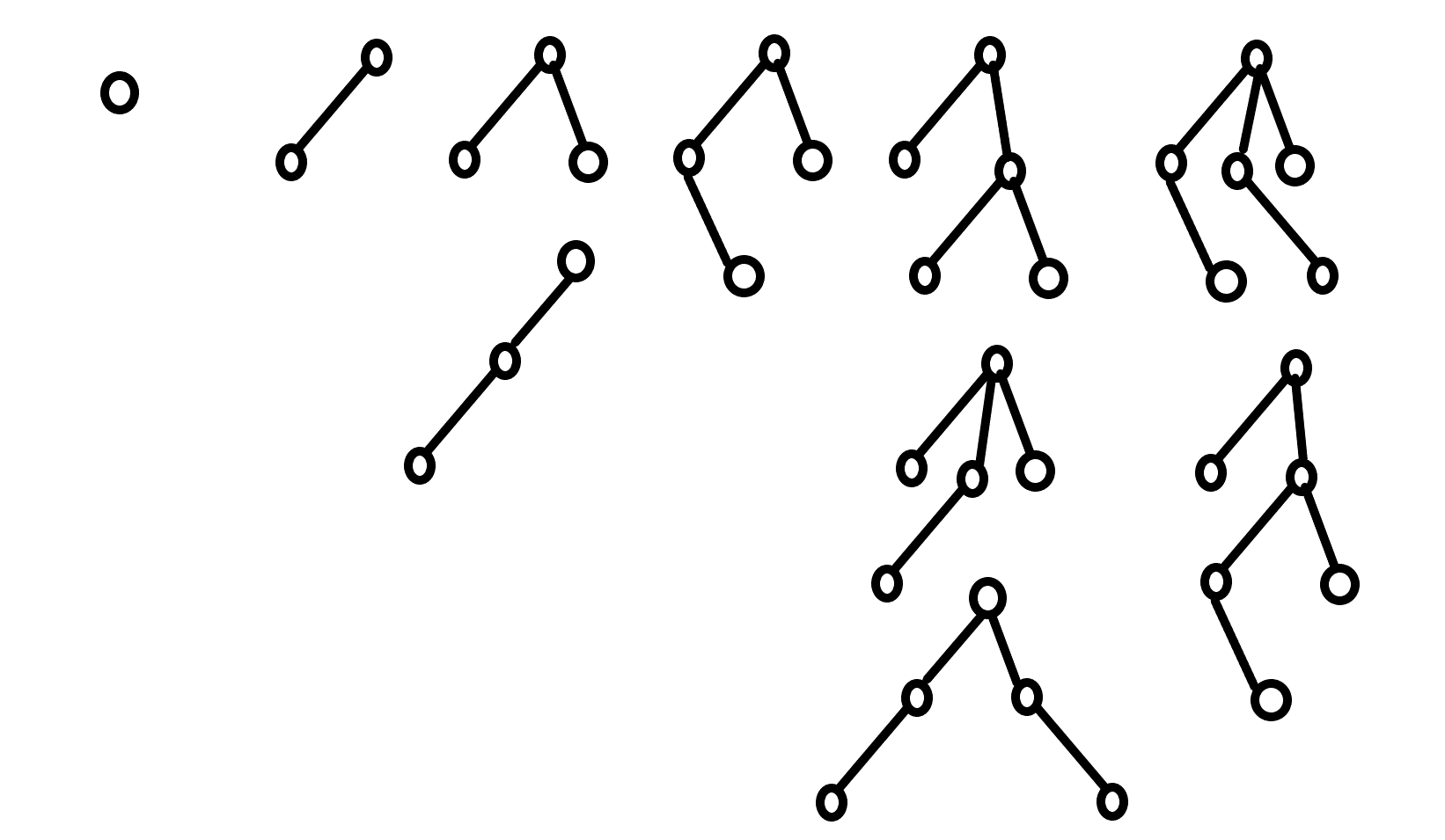
이렇게 만들어진 트리에는 특수한 속성이 있는데요, 바로
루트의 차수는 \(\lceil \log_2 N \rceil\)개를 넘지 않는다.
는 것입니다.
이제 \(N - 1\)회 비교한 후 다음번 구슬을 골라내기 위해 굳이 \(N - 2\)회 비교할 필요가 없습니다. 다음번 무거운 구슬을 골라내기 위해서는 루트의 자식들끼리만 비교하면 되거든요. 최대 \(\lfloor \log_2 N \rfloor\)번만 비교하면 다음번 무거운 구슬을 골라낼 수 있는 겁니다.
그런데 여기서, 문제가 생깁니다. 두 번째로 무거운 구슬을 골라낼 수는 있었습니다. 그렇다면 세 번째로 무거운 구슬을 골라내기 전 다시 트리를 만들어야 하는데, 여기서 비교 순서를 잘못 정하면 루트의 차수가 불필요하게 커질 수 있습니다.
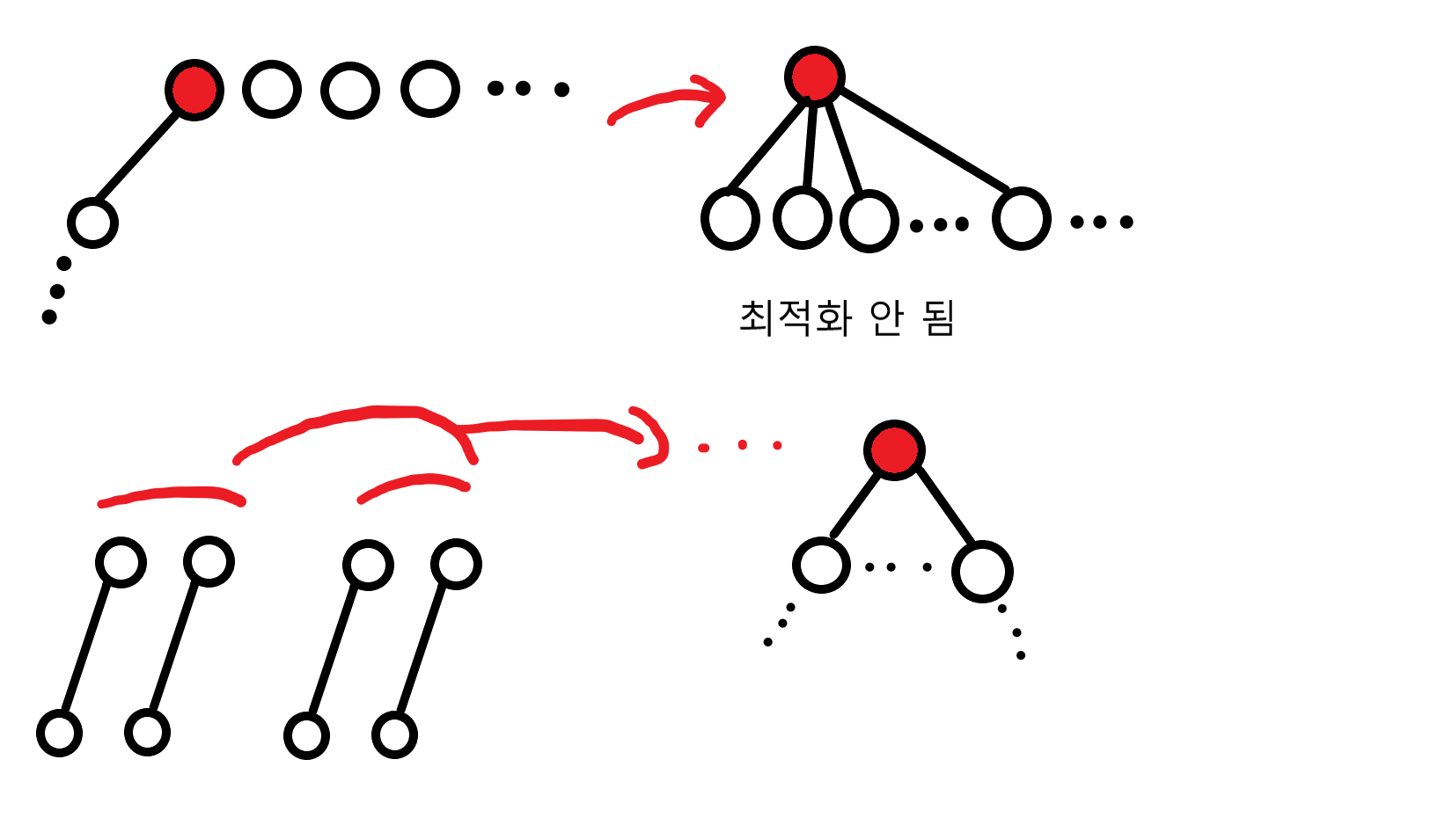
하필이면 처음 고른 구슬이 가장 무겁다면, 나머지 구슬들이 모두 밑으로 들어가버릴 수 있죠. 여기서 나름의 최적화가 필요한데요, 바로 차수가 낮은 자식들끼리 먼저 비교하는 것입니다. 비교 후 한 자식이 다른 자식 밑으로 들어가도 차수는 1 늘어날 뿐입니다.
차수가 낮은 자식들을 골라내는 것도 사실 만만치 않은 작업인데요, 저는 이 최적화를 위해 우선순위 큐를 쓰겠습니다. 최솟값을 골라내고 빈번히 삽입, 삭제하는데 시간복잡도 \(O(\log N)\)을 보장합니다.
이제 알고리즘을 만들어보겠습니다.
- 우선순위 큐에서 차수가 낮은 순으로 정점 2개를 골라 비교 후 병합, 다시 큐에 넣습니다.
- 우선순위 큐에 정점이 하나 남을 때까지 1을 반복합니다.
- 우선순위 큐에 정점이 하나 남았다면 꺼냅니다. 루트, 즉 가장 무거운 구슬을 골라냈습니다.
- K개의 구슬을 모두 골라냈다면 종료합니다. 그게 아니라면 5로 진행합니다.
- 루트의 자식들을 다 우선순위 큐에 넣습니다. 다시 1로 돌아갑니다.
그럼 한번 시간복잡도 계산을 해볼까요?
문제에서 주어진 시간제한은 \(0.4\)초. 1초는 대략 \(O(100,000,000)\)으로 계산합니다. (1억) 그렇다면 시간복잡도는 대략 \(40,000,000\)이하여야 합니다.
쿼리의 수는 \(K\)이고, 보통 시간복잡도 계산은 \(O(KM)\)입니다. 쿼리 \(K\)의 최대 크기는 10만, 두 번째 구슬부터는 골라내기 위한 비교횟수가 \(\log_2 N\)이고, 우선순위 큐에 \(\log_2 N\)개의 자식을 넣어서 \(\log_2 \log_2 N\)이므로
\[O(K\log N \log \log N) = 100,000 \times 16 \times 4 = 6,400,000\]제한 시간 내에 해결할 수 있음을 보장합니다. 또한 이 알고리즘의 구슬 최대 비교횟수는
\[K \log_2 N \lessapprox 1,600,000\]이므로 제한 횟수 내에 정렬이 완료됨을 보장합니다.
#include "biggest.h"
#include <vector>
#include <queue>
std::vector<int> children[100'001]; // 트리를 만들기 위한 벡터 배열
struct Comp {
bool operator()(int a, int b) {
return children[a].size() > children[b].size();
}
};
std::vector<int> biggest(int N, int K) {
std::vector<int> result;
std::priority_queue<int, std::vector<int>, Comp> pq; // 정점 차수가 낮은 순으로 골라냅니다
for (int i = 1; i <= N; ++i) pq.push(i);
while (result.size() != K) {
while (pq.size() != 1) { // 1 ~ 2. 2개를 골라낸 후 병합, 다시 넣기를 반복합니다.
int a = pq.top(); pq.pop();
int b = pq.top(); pq.pop();
if (compare(a, b) == a) { // 실제 저울을 사용하는 부분.
children[a].push_back(b);
pq.push(a);
}
else {
children[b].push_back(a);
pq.push(b);
}
}
int max = pq.top(); pq.pop(); // 3. 가장 무거운 구슬을 골라냅니다.
result.push_back(max); // 4. 구슬을 K개 골라냈다면 while 문을 빠져나갑니다.
for (const int& i : children[max]) pq.push(i); // 5. 자식을 모두 우선순위 큐에 넣습니다.
}
return result;
}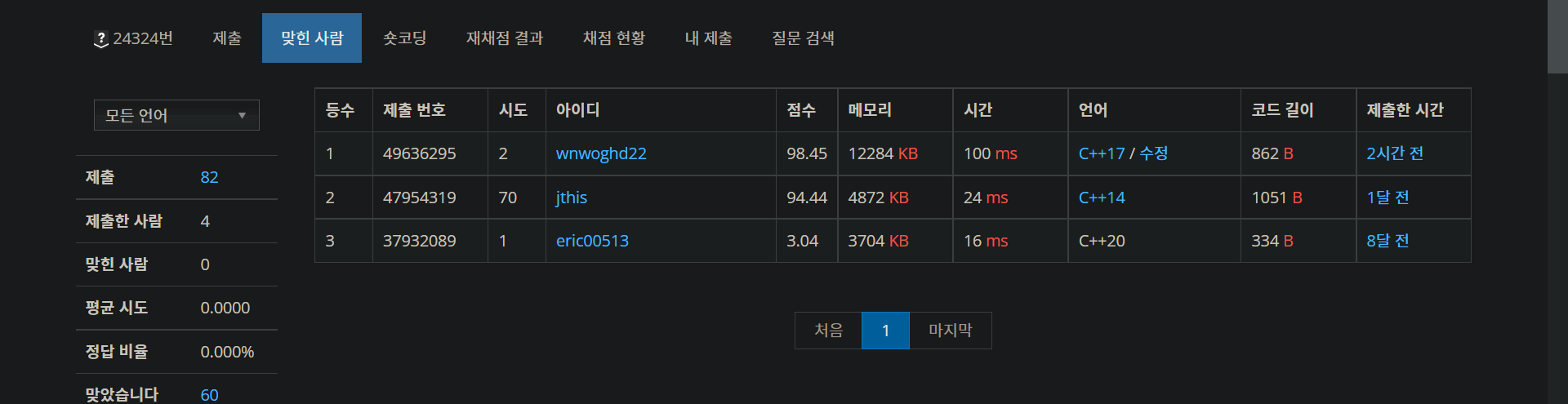
음… 100점은 어떻게 받는 거죠?