이번에 리뷰해볼 문제는 방사형 그래프입니다.

단계별로 풀어보기에서는 기하2로 분류되어있습니다. 8개의 능력치를 적절히 배치하여 볼록 다각형을 만들 수 있는지를 판단하면 되는 문제입니다.

일단 문제에서 주어진 배열의 길이는 8이고, 가능한 모든 배열에 대해 검사한다고 해도 \(8!=40,320\)이므로 시간 내에 충분히 해결 가능합니다. 이제 남은 과제는 볼록 다각형인지 판단하는 것 뿐이군요.

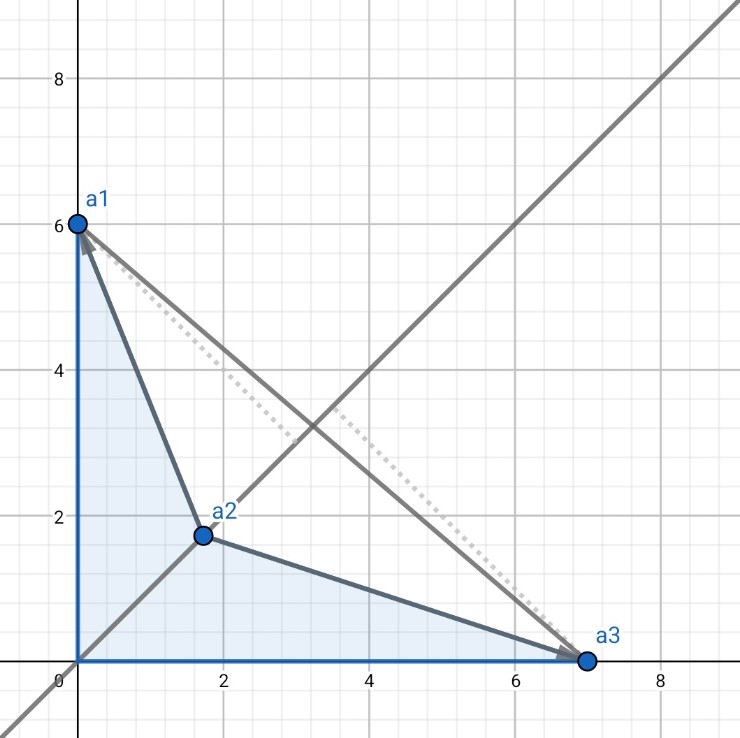
우선 8개 능력치가 \(45^\circ\) 간격으로 배치되어 있으므로 임의의 인접한 세 점을 그림으로 그리면 이렇게 됩니다.

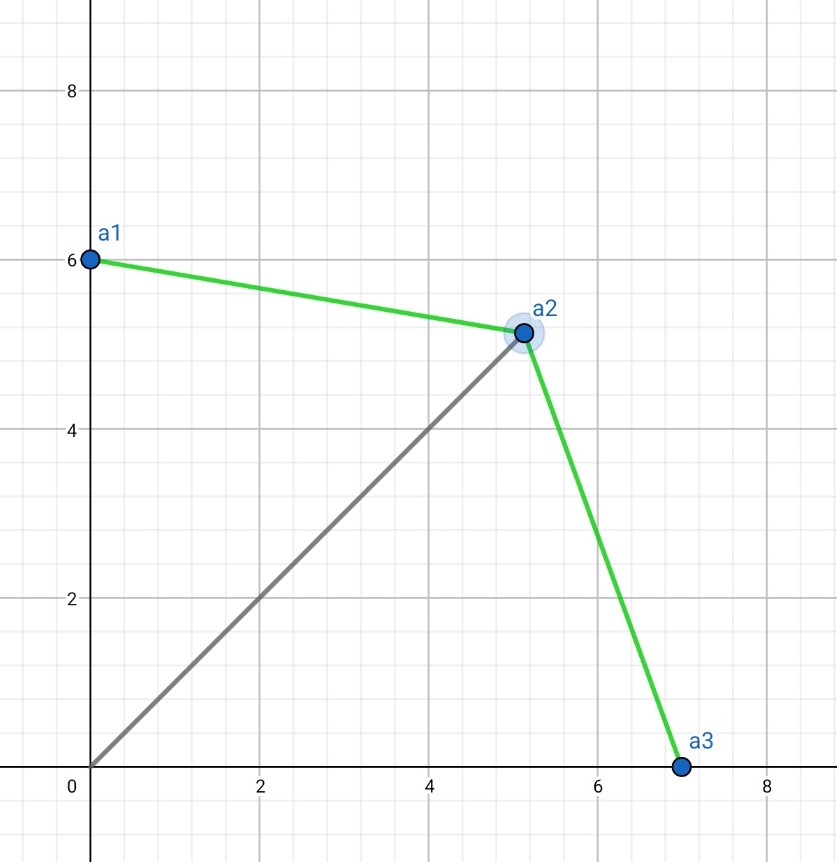
convex-edge

위의 그림은 각이 볼록일 때입니다. 만일 오목이라면 이렇게 되겠죠.

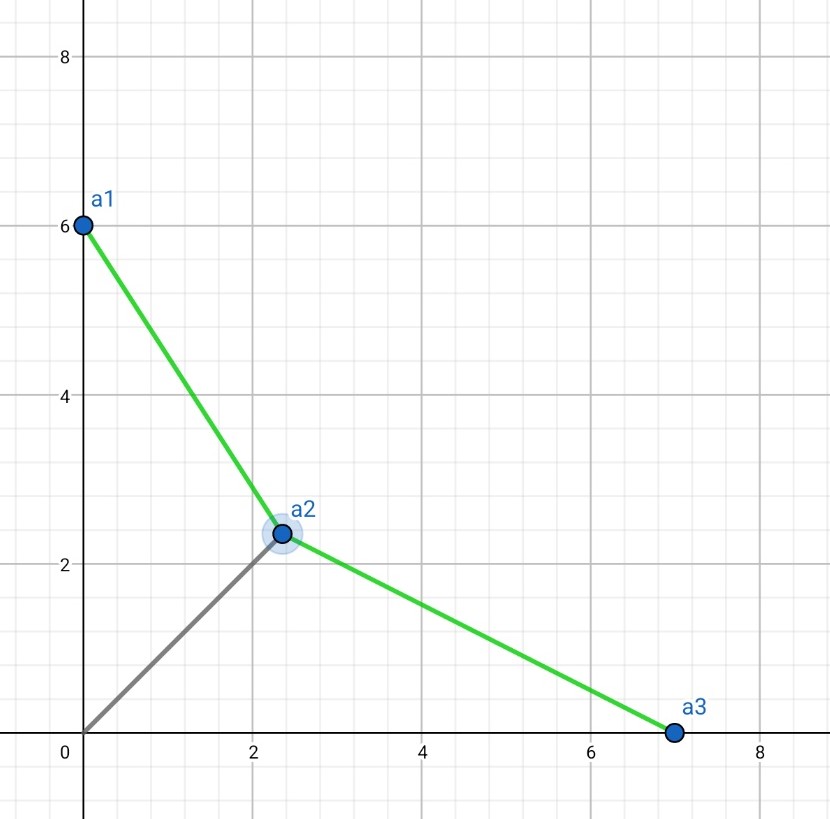
concave-edge

우리에게 관심이 있는 건 모든 임의의 점 \(a_1, a_2, a_3\)이 이루는 각이 볼록인지 아닌지입니다. 그리고 이를 판단하기 위해서 벡터의 외적을 쓰겠습니다.

\(a_2\)에서 \(a_1\)로의 벡터 \(\vec{V_1}\)과 \(a_2\)에서 \(a_3\)로의 벡터 \(\vec{V_2}\)를 그림으로 나타내면 다음과 같습니다.

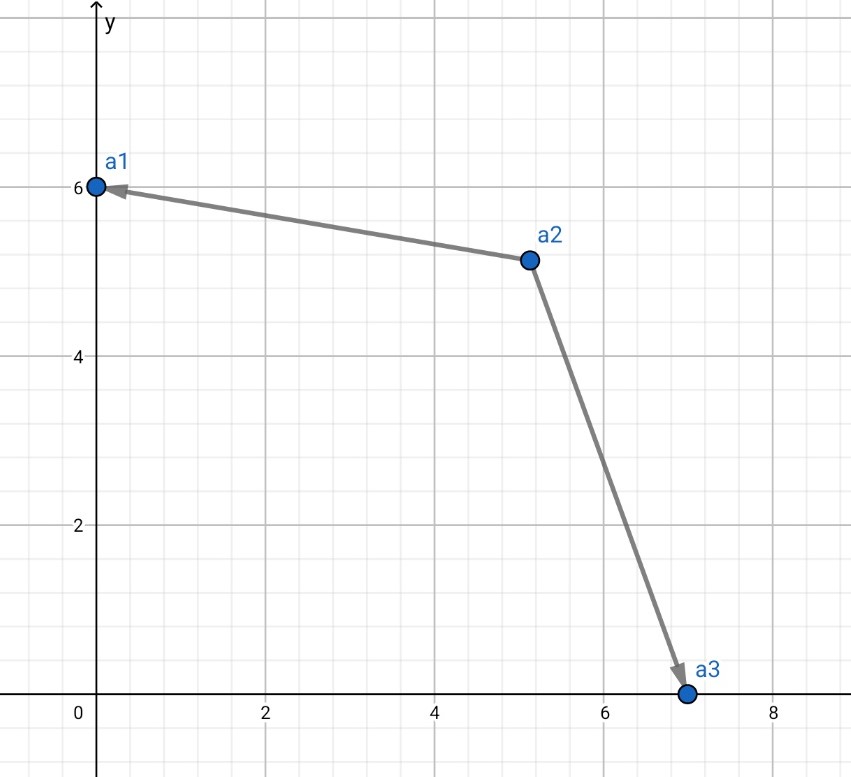
convex-vector

그리고 두 벡터간의 외적의 결과로 나온 3차원 벡터에서 우리가 알고 싶은 건 \(Z\)축 좌표의 값입니다. 이게 양수라면 두 각이 이루는 방향은 반시계 방향, 즉 볼록이고 음수라면 시계 방향으로 오목합니다.

두 벡터의 외적을 구해봅시다. \(\vec{V_1} = \langle x_1, y_1, z_1 \rangle, \vec{V_2} = \langle x_2, y_2, z_2 \rangle\)와 행렬

\[\begin{bmatrix} \hat{i} & \hat{j} & \hat{k} \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end{bmatrix}\]

에 대해, \(\vec{V_1} \times \vec{V_2} \)의 \(Z\)는

\[\hat{k} \times (x_1 y_2 - x_2 y_1)\]

로 구할 수 있습니다. 표준좌표계이므로 \(\hat{k}\)는 \(\langle 0,0,1 \rangle\)이고, 우리는 그냥 \(x_1 y_2 - x_2 y_1\)의 값을 구해주면 됩니다. 다시 돌아가봅시다. 세 능력치 \(a, b, c\)에 대해 각 점을

\[a_1 = (0, a), a_2 = (b / \sqrt{2}, b / \sqrt{2}), a_3 = (c, 0)\]

로 두겠습니다. 편의상 \(b / \sqrt{2}\)를 \(b’\)라 하겠습니다. 그렇게 되면

\[\vec{V_1} = \langle 0 - b', a - b', 0 \rangle, \vec{V_2} = \langle c - b', 0 - b', 0 \rangle\]

이 됩니다. 그리고

\[\begin{matrix} x_1 y_2 - x_2 y_1 &=& (0 - b')(0 - b') - (a - b')(c - b') \\ &=& b' ^ 2 - ac + b'(a + c) - b' ^ 2 \\ &=& b'(a + c) - ac \end{matrix}\]

결국 \(b(a + c)/\sqrt{2} - ac\)가 0보다 작다면, 두 벡터는 시계방향이므로 각이 오목해집니다.

bool CCW(double a, double b, double c) { return b / sqrt(2) * (a + c) < a * c; }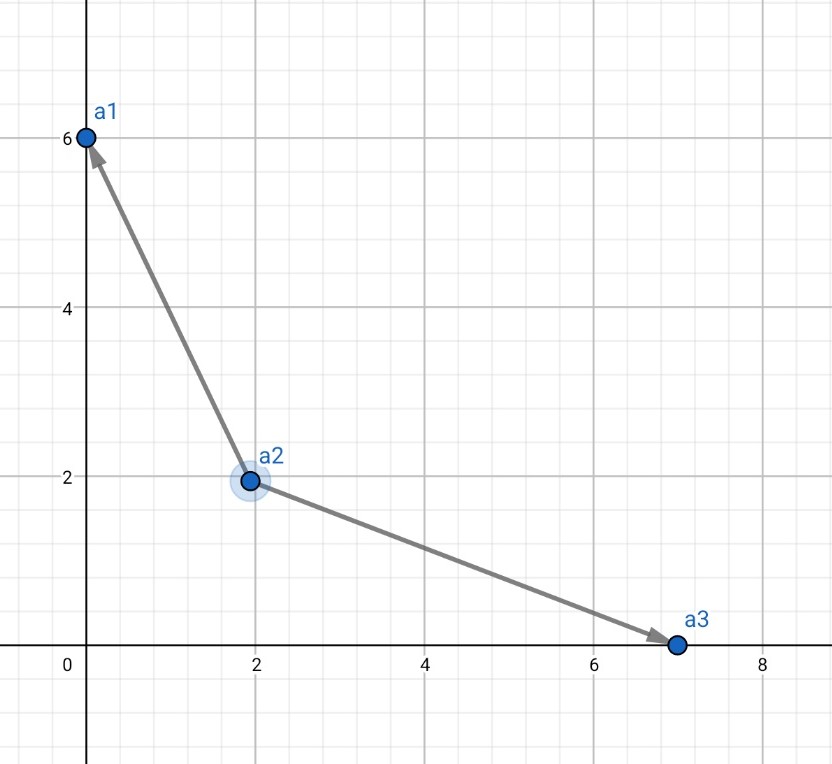

concave-vector

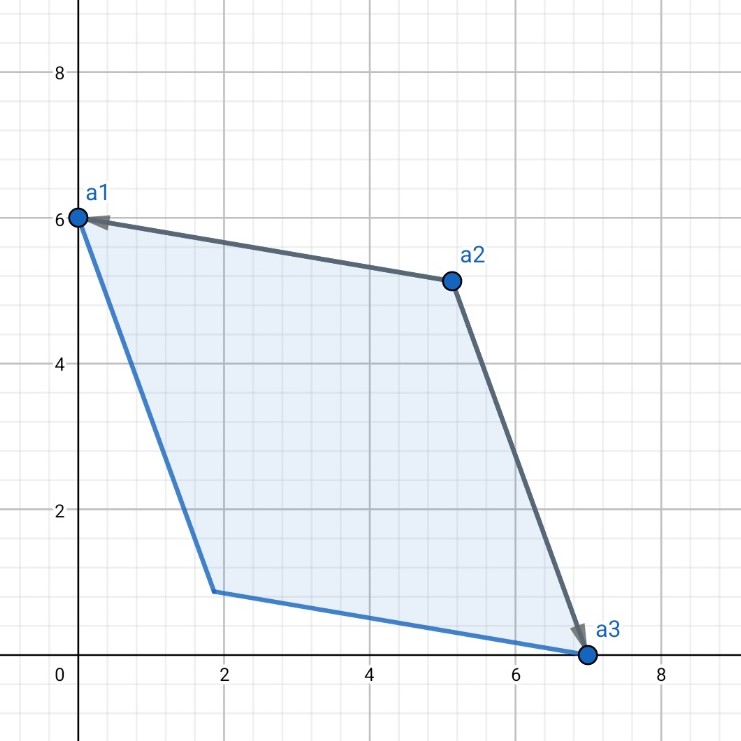
그런데, 변을 정리하여 얻게 된 식 \(b(a + c)/\sqrt{2} < ac\) 이, 뭔가 도형으로 설명이 될 것 같습니다.

\(ac\)는 사각형의 넓이가 되겠네요. 그리고 \(b(a + c)/\sqrt{2}\) 는 밑변의 길이 \(b\)에 대해 높이가 각각 \(a/\sqrt{2}, c/\sqrt{2}\) 인 삼각형 두 개를 더한 후 두 배를 한 것과 같습니다.

area

만일 볼록한 각이라면 두 삼각형의 넓이 합이 \(ac\)보다 클겁니다. 넓이 합이 \(ac\)보다 작다면 오목하겠죠. 그런데 어째서 외적을 계산했을 뿐인데 넓이가 유도된 걸까요?

외적의 본질

사실상 문제를 해결하는 데에 필요한 논의는 모두 끝났습니다. 하지만 좀 더 근본적인 이야기를 함으로써 더 깊이 이해하도록 해보죠.

우선 내적과 외적이 본질적으로 무엇을 하는 녀석들인지를 알 필요가 있습니다. 물리학적으로 내적은 당기기, 외적은 돌리기에 비유될 수 있습니다. 앞뒤로만 움직이는 물체에 비스듬히 힘을 줘 당길 때 물체에 가해지는 힘의 크기가 내적입니다. 그리고 한 점에 고정되어 돌아가는 물체에 비스듬히 힘을 줘 돌릴 때 순간적으로 물체에 가해지는 힘의 크기와 방향이 외적이죠. 그리고 외적의 계산 결과는 신기하게도 두 벡터가 그리는 평행사변형의 넓이가 됩니다.

result

이 평행사변형의 넓이는 어느 한 쪽으로 회전할 때 양의 넓이를 가지고, 반대쪽으로 회전할 때 음의 넓이를 갖습니다. 만일 돌리려는 벡터와 가해지는 힘의 방향이 같아 팽팽해지면 그 순간 가해지는 힘은 0이고, 평행사변형의 넓이도 0이 됩니다. 또한 이 넓이가 바로 외적의 결과로 나온 벡터의 \(Z\)축으로의 크기이기도 합니다. 식을 유도했더니 넓이가 나온 것도 바로 이런 이유죠.

#include <iostream>
#include <cmath>
#include <algorithm>

int input[8]; // 입력을 받을 배열
int perm[8]; // 모든 순열을 확인하기 위한 배열
int temp[10];

bool CCW(double a, double b, double c) { return b / sqrt(2) * (a + c) < a * c; }

int main() {
    int i, flag, result = 0;
    for (i = 0; i < 8; ++i) perm[i] = i, std::cin >> input[i];
    // perm = { 0, 1, 2, 3, 4, 5, 6, 7 }
    
    do {
        for (i = 0; i < 10; ++i)
            temp[i] = input[perm[i % 8]];
        // temp = { a1, a2, a3, a4, a5, a6, a7, a8, a1, a2 }
        // 뒤에 a1, a2를 덧붙이는 것은 for문으로 간단하게 훑기 위함입니다.

        flag = true;
        for (i = 0; i < 8; ++i) {
            if (CCW(temp[i], temp[i + 1], temp[i + 2])) { // 만일 오목한 각이 하나라도 나온다면
                flag = false;
                break; // 즉시 그 순열에 대한 검사를 종료합니다.
            }
        }
        result += flag;
    } while (std::next_permutation(perm, perm + 8)); // 모든 순열에 대해 검사합니다.

    std::cout << result;
    
    return 0;
}

Categories

외적의 본질